$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
概要
量子プログラミングはざっくりと以下の手順で計算を解く認識です。
手計算→実装→実装結果と手計算の結果をすり合わせる。
なので自分の復習のためにどのような計算を行うか記述してみました。
また自分の持っている入門書では数式が優しく書かれているが、細かい計算の仕方が足りないなと感じる部分もあったため取り組んでみました。
量子回路
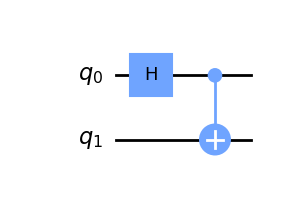
前回使用した回路で使われる計算を書いてみる
https://qiita.com/Y10-JP/items/7f826277d95b422f281c
from qiskit import QuantumCircuit
import matplotlib.pyplot as plt
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
qc.draw('mpl')
前提知識
量子プログラミングの特徴でよくキーワードは
・状態の重ね合わせ
・量子もつれ
だと思います。
まず状態の重ね合わせがどのような状態か説明します
1量子bit系
まずは1量子bit系の計算について説明します。
画像で言う$q_0$(または$q_1$)のみの状態について注目した場合です。
状態の重ね合わせ
古典コンピューターで1bitが持てる状態は 0 or 1 の二通りで、0と1を切り替える必要があります。
それに比べ、量子コンピューターでは1bitが持つ状態には0と1の両方が含まれています。
このことを状態の重ね合わせと呼びます。
1bitが持つ状態を式に表すと以下の式になります
q_0:\ket{\psi} = \alpha\ket{0} + \beta\ket{1}
$ \ket{\psi} $:1bitが持つ状態
$ \ket{0} $:古典で言う0の状態
$ \ket{1} $:古典で言う1の状態
$ \alpha,\beta$:複素数
また、$ \ket{0} $と$ \ket{1} $は状態の最小単位で標準基底と呼びます。
$ \ket{\psi} $がいかなる状態であろうと上記の式で表せます。
ベクトル
量子bitの状態はベクトルで定義できます。
状態の最小単位である$ \ket{0} $と$ \ket{1} $をベクトルに直すとそれぞれ
$$$$
\begin{align*}
\ket{0} =
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right) \\
\ket{1} =
\left(
\begin{array}{c}
0 \\
1
\end{array}
\right)
\end{align*} \\
と表せます。
なので状態は
\begin{align}
\ket{\psi} & = \alpha\ket{0} + \beta\ket{1} \\
& = \alpha
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right) + \beta\
\left(
\begin{array}{c}
0 \\
1
\end{array}
\right)
= \left(
\begin{array}{c}
\alpha \\
\beta\
\end{array}
\right)
\end{align}
と書けます。
状態の決定
ではどのようにして状態が定まるのでしょうか?
答えは確率です。1bitが持つ状態を測定した時、量子bitの状態は確率に沿って$ \ket{0} $or$ \ket{1} $に状態が定まります。
このように量子プログラミングにおいて確率は非常に重要な要素です。
手計算の段階で任意の状態の確率を操作する必要があります。
1bitが持つ状態が$ \ket{0} $or$ \ket{1} $それぞれになる確率は、先ほどの状態の式を用いて次のように計算できます。
・$ \ket{0} $になる確率
\begin{align}
\left|\braket{0}{\psi}\right|^2 & = \left|\bra{0}\left(\alpha\ket{0} + \beta\ket{1}\right)\right|^2 \\
& = \left|\alpha
(1, 0)
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right) + \beta
(1, 0)
\left(
\begin{array}{c}
0 \\
1
\end{array}
\right) \right|^2 \\
& = \left|\alpha\cdot1+\alpha\cdot0\right|^2 \\
& = \left|\alpha\right|^2 ( \left|\alpha\right|^2 = \alpha\cdot\alpha^* )
\end{align}
・$ \ket{1} $になる確率
\begin{align}
\left|\braket{1}{\psi}\right|^2 & = \left|\bra{1}\left(\alpha\ket{0} + \beta\ket{1}\right)\right|^2 \\
& = \left|\alpha
(0, 1)
\left(
\begin{array}{c}
1 \\
0
\end{array}
\right) + \beta
(0, 1)
\left(
\begin{array}{c}
0 \\
1
\end{array}
\right) \right|^2 \\
& = \left|\beta\cdot0+\beta\cdot1\right|^2 \\
& = \left|\beta\right|^2 ( \left|\beta\right|^2 = \beta\cdot\beta^* )
\end{align}
・$ \ket{0} $の$ \ket{1} $確率分布
\begin{align}
\left|\braket{\psi}{\psi}\right|^2 & = \alpha\ket{0} + \beta\ket{1} \\
& = \left|\alpha\right|^2 + \left|\beta\right|^2
\end{align}
以上のように個々の確率の計算は1bitの状態ケットの右からブラを作用させることで求めることが出来ます。
また、それぞれの標準基底に付いていた$\alpha$,$\beta$の二乗が確率となることも分かります。
全ての取りうる値の確率の総和は"1"になる必要があるため以下の関係式が求まります。
\begin{align}
1 & = \left|\alpha\right|^2 + \left|\beta\right|^2
\end{align}
以上で1量子bit系で必要な計算の説明は終わりです。
2量子bit系 ~n量子bit系
次に2量子bit系の計算について説明します。
画像で言う$q_0$と$q_1$両方の状態について注目した場合です。

状態の重ね合わせ
まずはそれぞれの量子bitの状態を表記します。
q_0:\ket{\psi}_0 = \alpha_0\ket{0} + \beta_0\ket{1}\\
q_1:\ket{\psi}_1 = \alpha_1\ket{0} + \beta_1\ket{1}
個々の量子bitの状態は、テンソル積を使って以下のように表現を変えることができます。
\begin{align}
\ket{\psi}_0\otimes\ket{\psi}_1
& = (\alpha_0\ket{0} + \beta_0\ket{1})\otimes(\alpha_1\ket{0} + \beta_1\ket{1}) \\
& = \alpha_0\alpha_1\ket{0}\otimes\ket{0} + \alpha_0\beta_1\ket{0}\otimes\ket{1} +
\beta_0\alpha_1\ket{1}\otimes\ket{0} +
\beta_0\beta_1\ket{1}\otimes\ket{1} \\
& = \alpha_0\alpha_1\ket{00} + \alpha_0\beta_1\ket{01} +
\beta_0\alpha_1\ket{10} + \beta_0\beta_1\ket{11}
\end{align}
以上の式が2量子bit系の状態を表しています。
$\ket{00}$,$\ket{01}$,$\ket{10}$,$\ket{11}$は2量子bit系の標準基底です。
標準基底の個数は1量子bit系で2個、2量子bit系で4個...と増えていきます。
なので、n量子bit系での標準基底の数は$2^n$個となります。
n量子bit系の状態は複素数は$c_0,$$c_1,$$\ldots,$$c_{n-1}$、$\ket{00\ldots00},\ldots$$,\ket{11\ldots11}$となるので
\begin{align}
\ket{\psi}_{all}
& = \ket{\psi}_0\otimes\ket{\psi}_1\otimes\ldots\otimes\ket{\psi}_{n-1} \\
& = \displaystyle \sum_{i=0}^{n-1} c_{i}\ket{i} \\
&(\ket{i}=\overbrace{\overbrace{\ket{00\ldots00}}^{ n個 }~\ket{11\ldots11}}^{ n個 })
\end{align}
となる。
ベクトル
2量子bitの状態をベクトルで表す場合、テンソル積の計算を行わなければいけません。
2量子bit系のテンソル積の計算例は以下のようになります。
$$$$
\ket{\alpha} = \left(
\begin{array}{c}
\alpha_0 \\
\alpha_1
\end{array}
\right)\\
\ket{\beta} =
\left(\begin{array}{c}
\beta_0 \\
\beta_1
\end{array}
\right)\\
\ket{\alpha}\otimes\ket{\beta} =
\Bigg(\begin{array}{c}
\alpha_0\left(
\begin{array}{c}
\beta_0 \\
\beta_1
\end{array}
\right) \\
\alpha_1\left(
\begin{array}{c}
\beta_0 \\
\beta_1
\end{array}
\right)
\end{array}\Bigg) \\
=\left(
\begin{array}{c}
\alpha_0\beta_0 \\
\alpha_0\beta_1 \\
\alpha_1\beta_0 \\
\alpha_1\beta_1
\end{array}
\right) \\
具体的な数値は \\
\ket{00}=\left(
\begin{array}{c}
1 \\
0 \\
0 \\
0
\end{array}
\right),
\ket{01}=\left(
\begin{array}{c}
0 \\
1 \\
0 \\
0
\end{array}
\right),
\ket{10}=\left(
\begin{array}{c}
0 \\
0 \\
1 \\
0
\end{array}
\right),
\ket{11}=\left(
\begin{array}{c}
0 \\
0 \\
0 \\
1
\end{array}
\right)
状態の決定
長くなってしまうので、ここでは1例を挙げます。計算は1量子bit系の時とさほど変化はありません。
・$ \ket{00} $になる確率
\begin{align}
\left|\braket{00}{\psi_{all}}\right|^2 & = \left|\braket{00}{\ket{\psi}_0\otimes\ket{\psi}_1}\right|^2
\\ & = \left|\braket{00}{(\alpha_0\alpha_1\ket{00} + \alpha_0\beta_1\ket{01} + \beta_0\alpha_1\ket{10} + \beta_0\beta_1\ket{11})}\right|^2
\\ & = \left|\alpha_0\alpha_1\right|^2 \\
\end{align}
・$ \ket{01} $になる確率
\begin{align}
\left|\braket{01}{\psi_{all}}\right|^2
& = \left|\alpha_0\beta_1\right|^2 \\
\end{align}
・$ \ket{10} $になる確率
\begin{align}
\left|\braket{01}{\psi_{all}}\right|^2
& = \left|\beta_0\alpha_1\right|^2 \\
\end{align}
・$ \ket{11} $になる確率
\begin{align}
\left|\braket{01}{\psi_{all}}\right|^2
& = \left|\beta_0\beta_1\right|^2 \\
\end{align}
多量子bit系においてもそれぞれの標準基底に付いていた複素数の二乗が確率となることも分かり、その総和は1になります。
\begin{align}
1 = \left|\alpha_0\alpha_1\right|^2+\left|\alpha_0\beta_1\right|^2+\left|\beta_0\alpha_1\right|^2+\left|\beta_0\beta_1\right|^2
\end{align}
終わりに
こういったものは初めてなので、雑な部分が多いと思います。
ぜひ、加筆・修正をコメントなどでしていただけるとありがたいです。
ここまで読んでいただいてありがとうございますmm