台車型倒立振子の運動方程式をNewton-Euler法で導出します.モデルは,川田昌克 編著の「倒立振子で学ぶ制御工学(森北出版株式会社)」を参考にしました.
Free-Body-Diagramと物理パラメータの定義
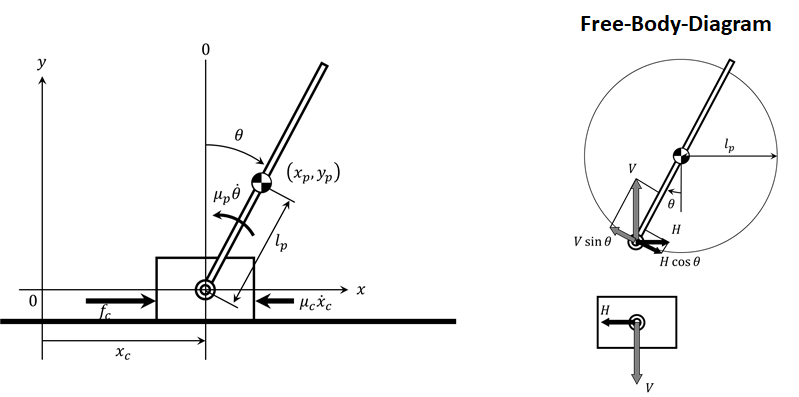
下の図が,台車型倒立振子に働く力やトルクを示したものです.また,台車型倒立振子の物理パラメータを表で示しました.
| 台車の質量 | 振子の質量 | 振子の重心まわりの慣性モーメント | 重力加速度 |
|---|---|---|---|
| $m_c , \rm [kg]$ | $m_p , \rm [kg]$ | $J_p , \rm [kg \cdot m^2]$ | $g , \rm [m/s^2]$ |
| 台車の粘性摩擦係数 | 振子の粘性摩擦係数 | 振子の軸から重心までの長さ |
|---|---|---|
| $\mu_c , \rm [kg/s]$ | $\mu_p , [\rm kg \cdot \rm m^2/s]$ | $l_p , \rm [m]$ |
台車の位置は $y$ 軸から台車の中心までの距離とし,$x_c , \rm [m]$ と定義します.また,振子の角度は鉛直方向から時計回りを正とし,$\theta , \rm [rad]$ と定義します.$f_c$ の力で台車を押し,左右に動くと振子には水平方向に$ H , \rm [N]$,鉛直方向に $V , \rm [N]$ の力が加わります.同時に作用反作用の法則より,台車にも水平方向に $H , \rm [N]$,垂直方向に $V , \rm [N]$の力が加わります.
運動方程式の導出
Free-Body-Diagram をもとに運動方程式を導出していきます.まずは台車と振子のそれぞれの運動方程式を記述します.台車の水平方向の運動方程式は,粘性摩擦を考慮して次のようになります.
m_c\ddot{x}_c=f_c-\mu_c\dot{x}_c-H \tag{1}
振子の水平方向,鉛直方向の運動方程式はそれぞれ
\left \{
\begin{array}{l}
m_p\ddot{x}_p=H
\\
m_p\ddot{y}_p=V-m_pg
\end{array}
\right. \tag{2}
となります.また,重心まわりの回転の運動方程式は,次のようになります.
$$
J_p\ddot{\theta}=-\mu_p\dot{\theta}+Vl_p\sin \theta-Hl_p\cos\theta \tag{3}
$$
これで台車と振子の運動方程式が得られたのですが,振子の座標である $x_p$ と $y_p$ は振子の角度 $\theta$ を用いて書き換えることができます.
\left \{
\begin{array}{l}
x_p=x_c+l_p\sin \theta
\\
y_p=l_p\cos \theta
\end{array}
\right. \tag{4}
$x_p, , y_p$の1階微分と2階微分を計算すると,それぞれ式$(5), , (6)$になります.
\begin{equation}
\left \{
\begin{array}{l}
\dot{x}_p=\dot{x}_c+l_p\dot{\theta}\cos \theta
\\
\dot{y}_p=-l_p\dot{\theta}\sin \theta
\end{array}
\right.
\end{equation} \tag{5}
\begin{equation}
\left \{
\begin{array}{l}
\ddot{x}_p=\ddot{x}_c+l_p(\ddot{\theta}\cos \theta-\dot{\theta}^2 \sin \theta)
\\
\ddot{y}_p=-l_p (\ddot{\theta} \sin \theta+\dot{\theta}^2 \cos \theta)
\end{array}
\right.
\end{equation} \tag{6}
式$(2)$に式$(6)$を代入すると,$H, \, V$は次のように表されます.
\begin{equation}
\left \{
\begin{array}{l}
H=m_p\ddot{x}_c+l_p(\ddot{\theta}\cos \theta-\dot{\theta}^2 \sin \theta)
\\
V=-m_pl_p\ddot{\theta}\sin \theta-m_pl_p\dot{\theta}^2\cos \theta+m_pg
\end{array}
\right.
\end{equation} \tag{7}
式 $(7)$ を,台車の水平方向の運動方程式である式 $(1)$ と,振子の重心回りの回転方向の運動方程式である式 $(3)$ に代入して $H, , V$ を消去して式変形すると,最終的に台車型倒立振子の非線形モデルが得られます.
台車型倒立振子の非線形モデル
\left {
\begin{array}{l}
(m_c+m_p)\ddot{x}_c+m_pl_p\ddot{\theta}\cos \theta=-\mu_c\dot{x}_c+m_pl_p\dot{\theta}^2\sin \theta+f_c\
\
m_pl_p\ddot{x}_c\cos \theta+(J_p+m_pl_p^2)\ddot{\theta}=-\mu_p\dot{\theta}+m_pgl_p\sin \theta
\end{array}
\right.