はじめに
共役勾配法による計算で収束しない問題が発生し、自分のバグなのかこの2週間くらいすごい悩みました。収束の様子について少しプロットした見たので、そのメモです。
コードは下記に置いてあります。
共役勾配法の収束
共役勾配法は正定値行列Aとベクトルbが与えられたとき、Ax=b を解く計算方法です。いろいろ解説があるので、中身はそちらに譲ります。
- 解 x を基底 $p_k$ の線形結合で表す。
- $p_k$ をiterativeに求めていく。$x_{k+1}=x_k + \alpha_k p_k$ とし係数$\alpha_k$ を求める。
- 残差$r_k=b-A*x_k$を最終的 0 にする。
- step k での残差$r_{k+1}=r_k - \alpha p_k$ を更新していく
- Aによる内積を計量とする空間での直交化で $p_{k+1}=r_k+\beta p_k$を求める
コードは公開していますが、計算部分はこんな感じです。
def solve(A, b):
dim = len(b)
x = np.zeros(dim) # initial_value
r = b - np.dot(A, x)
p = r
r_ss = np.dot(r.T, r)
k = 0
while True:
# Calculate A*p
Ap = np.dot(A, p)
# Add base vector p and add projection to solution
_a = np.dot(r.T, p) / np.dot(p.T, Ap)
x = x + _a * p
r = r - _a * Ap
r_ss_temp = np.dot(r.T, r)
if np.abs(r_ss_temp) < 1.0E-10:
break
#
_b = r_ss_temp / r_ss
p = r + _b * p
r_ss = r_ss_temp
k = k + 1
return x
気になったこと
- 残差ベクトルが小さくなっていくか
- $\alpha$, $\beta$はどうなっているのかな
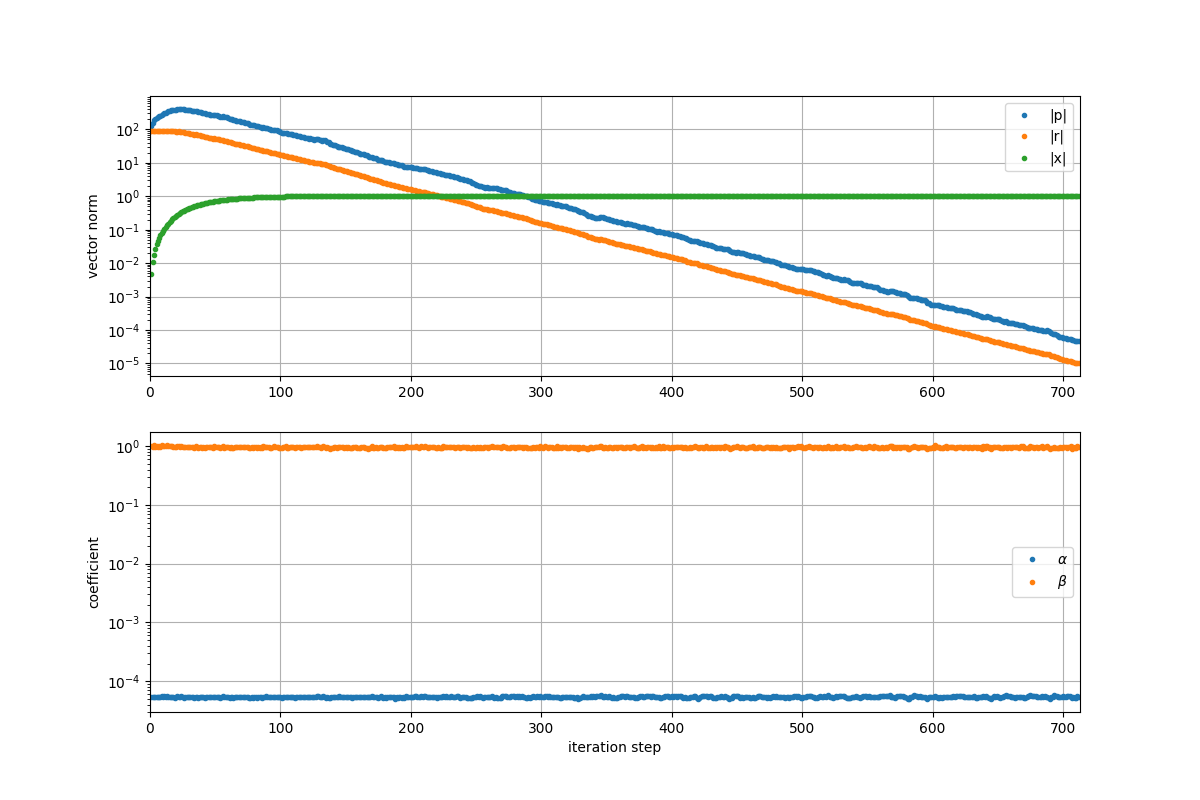
と気になったので、8192次元で、乱数を使った簡単な係数を解いた結果をプロットしてみました。
ここだと$\alpha$, $\beta$はほぼ同じスケールでした。
ほー、と思ったのは、
- 残差が小さくなるとともに、基底ベクトル$p$の大きさも小さくなっている
ことです。step の後半で $\alpha$のスケールが変わらないまま $p_k$ が小さいということは
- 後半の更新では解 $x$ をほとんど変化させていない
ということに対応します。なので、最後のあたりはほぼ効いていないであり、問題によっては初期値に依存する(全体が凸であるならglobal optimum に収束するのことが保証されているので依存性は関係ないが)かなと思いました。
収束しないとき
収束しない場合は
- 共役勾配法を使うための条件であるAが「対称正定値行列」を満たしていなかった
ということなのかなと思います。非線形な目的関数を2次近似して解いている場合、Hessian 行列は対称行列だから、最適解の付近なので凸だからと思っても、
- 高次の項の影響がある
- 実は凸ではなく、局所最適解でない
のであれば、成り立たないこともありますよね。また、正定値にするために、対角成分を嵩上げ($A^\prime =A + \lambda I$)したとしても、対称である条件を満たしていないと悪さをすることがあるようです。
まとめ
いろいろ条件を変えたけれど、収束性については一応納得できてきました。数学的にしっかり考えているような文献もあるので、時間があれば読んで考えてみたい気もします。Wikipediaにも convergence properties の記述があります。
(2022/12/15)