はじめに
最適化問題で、制約条件のもとでノルムを最小にする解を求めたいことがよくあります。そのとき、単純にノルムではなく微分したノルムを最小化することもあります。何故微分をするのか、というと、「滑らか」な解を求めたいからです。
- 微分フィルタは高周波を強調した信号になる
- 高周波を強調した信号のノルムを最小化する
- よって低周波が強調された「滑らかな」信号が求められる
で、どれくらいの拘束なのかなー、ということで、FFTしてパワーを見てみました。
内容
ある信号$x[n]$ に対して、フィルタ$h[n]$ を畳み込みます。
numpy の fft についてこちらに仕様が書かれています。
FFTして絶対値をとって、逆数を計算してみました。ただそれだけです。
import matplotlib.pyplot as plt
import numpy as np
N = 32
h = np.zeros(N)
h[0:2] = [1.0, -1.0]
h_steps = np.arange(N)
h_sp = np.fft.fft(h)
fig = plt.figure(figsize=(12, 6), layout='constrained')
fig.suptitle(f"Filter Gain (N={N})")
axs = fig.subplot_mosaic([["filter", "magnitude", "inv_mag"]])
axs["filter"].set_title(r"Filter $a[i]$")
axs["filter"].stem(h_steps[0:N+1], h[0:N+1])
axs["filter"].set_xlabel(r"$i$")
axs["filter"].set_ylim([-1.1, 1.1])
axs["filter"].grid(True)
axs["magnitude"].set_title(r"$|A[k]|^2$")
axs["magnitude"].plot(np.absolute(h_sp)[0:N//2+1], "o", markersize=5)
axs["magnitude"].grid(True)
axs["magnitude"].set_xlabel(r"$k$")
axs["magnitude"].set_xticks([0, (N//2)//2, N//2])
axs["magnitude"].set_xticklabels([f"{i}" for i in [0, (N//2)//2, N//2]])
axs["inv_mag"].set_title(r"$\frac{1}{|A[k]|^2}$")
axs["inv_mag"].plot([i for i in range(1,N//2+1)], 1.0/np.absolute(h_sp)[1:N//2+1], "o", markersize=5)
axs["inv_mag"].grid(True)
axs["inv_mag"].set_xlabel(r"$k$")
axs["inv_mag"].set_xticks([0, (N//2)//2, N//2])
axs["inv_mag"].set_xticklabels([f"{i}" for i in [0, (N//2)//2, N//2]])
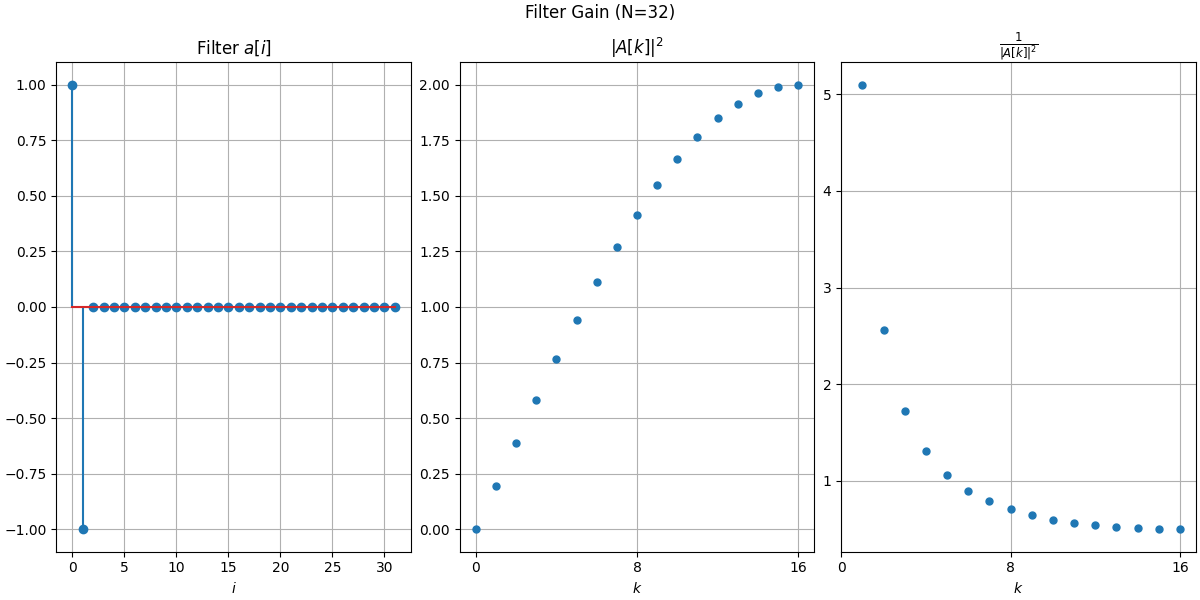
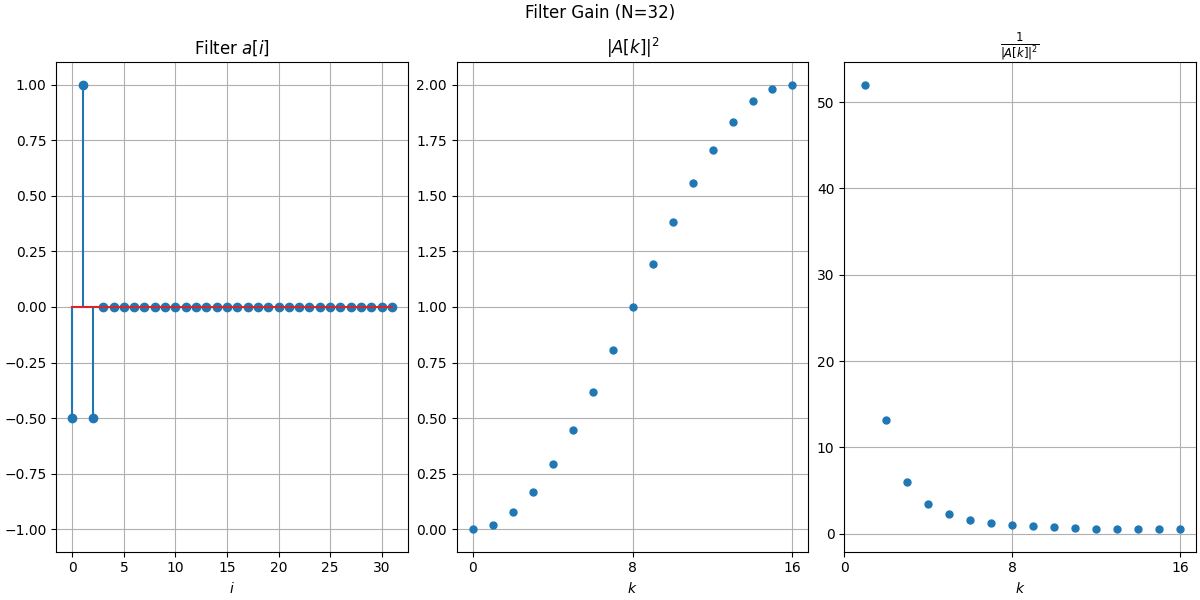
差分、ラブラシアンをそれぞれプロットしてみました。
周波数領域で$k=0$のとき$A[k]=0$なので、逆数をとったら発散しますね。こういうのを確か極って言うんだよね。
フィルタの形は、プロットをみればわかると思います。
まとめ
FFTしてみた。紙と鉛筆で計算したら、もう少し理論的なことを言えるかもしれないけれど、とりあえず実験的にプロットしてみたのでメモしました。
おれは何をしているのだろう。。。
(2024/2/4)
捕捉: matplotlib で便利な関数が用意されているので、それを使うのがよいかも。
https://matplotlib.org/stable/gallery/lines_bars_and_markers/spectrum_demo.html