基礎的なことを再考してみたくて。ノートに書くと失くすので、ここに書いてみよう。
メモ概要
- 位置をスムージングさせるカルマンフィルタを、最も単純な例題として考えてみる。
- 誤差のベイズ推定として導出する。
- 1次元で、状態も観測も位置とする
- 初期状態の推定についてのふるまいをシミュレーションでみてみたい
1次元の運動の位置の定式化
誤差の分散の時間変化
時刻$t_n$の位置を$x_n$とあらわすことにする。時刻$t_n$から時刻$t_{n+1}$にかけての移動量を$u_n$とする。
x_{n+1}=x_n + u_n
つぎに、位置と移動量について、真値からの誤差を考える。誤差は位置の真値$x^*$と推定値$\hat{x}$の差で定義する。
\delta x = x^* - \hat{x} \\
\delta u = u^* - \hat{u} \\
これから
\delta x_{n+1} = \delta x_n + \delta u_n
を得る。この誤差の分散は、位置と移動量が無相関であると仮定すると
V[\delta x_{n+1}] = V[\delta x_n] + V[\delta u_n]
と書ける。$x$の分散を$P$、$u$の分散を$Q$と書くことにすると
P_{n+1} = P_{n} + Q_n
となる。今、初期の位置$x_0$と誤差の分散$P_0$、移動量の分散$Q$はモデルで与えられているとする。$P_n$は時間とともに、移動量の曖昧性$Q$が蓄積されてどんどん大きくなっていく。
ベイズ推定による状態と誤差共分散の更新
次に、状態変数の位置が$x_n$であるとき、位置について観測$y_n$を得たとする。観測には誤差$\epsilon$があり、この誤差は
y = x + \epsilon \\
\epsilon \sim N(0, R)
に従うとする。$N$は正規分布を表す。
今、$x_n$は観測$y_n$を得る前であるとすると、そのときの誤差の確率分布は、
P(\delta x) = N(0, P)
であるとする。この$x$のとき、位置$y$を観測する確率は、$\Delta y = y - x$として
P(\Delta y | \delta x) = N(0,R)
である。では、$y$を観測した後で最も尤もらしい$\delta x$を求めるには、
\hat{\delta x} = \underset{\delta x}{\textrm{argmax}} P(\delta x|\Delta y)
である。 ベイズの定理(Bayes's theorem) より
P(\delta x|\Delta y) = \frac{P(\Delta y | \delta x) P(\delta x)}{P(\Delta y)}
であるので、
\begin{align}
\log P(\delta x | y) &= -\frac{1}{2\pi} \left[ \frac{(\Delta y - \delta x)^2}{R} + \frac{(\delta x)^2}{P} \right ] + const. \\
&= -\frac{1}{2\pi} (R^{-1} + P^{-1})\left(\delta x - \frac{R^{-1} y}{R^{-1}+P^{-1}} \right)^2 + const.
\end{align}
から
\hat{\delta x} = \frac{P}{P+R} \Delta y
を得る。また、このときの事後確率を最大化したときの事後分布$P(\delta x|\Delta y)$の分散は、
\hat{P}^{-1} = R^{-1} + P^{-1}
と得る。これを用いて状態変数$x$を更新したいので、つまり$K=\frac{P}{P+R}$とおいて、状態変数と誤差の分散の更新式を得る。
x \leftarrow x + K(y-x) \\
P \leftarrow P(1-K)
モデルによる観測値の生成 (simulation)
次に、この運動モデルと誤差モデルによって生成される観測値を計算してみる。
-
運動は初期値 $x_0=x(t_0)$ と制御項 $u_n=u^*(t_n)$ の真値から生成できる。ただし、実際は運動方程式$d/dt x(t) = v(t)$で記述されている運動を$u_n=v(t_n)\Delta t$で離散化していると考える。
-
実際に観測される制御項には正規分布に従うノイズが乗っている
u_n=u_n^*+\epsilon \\
\epsilon \sim N(0,Q)
ウィナー過程(確率過程)あるいはノイズ密度から$Q$を計算することができるが、それはまた別の機会にまとめます。
- 観測は真値に対してノイズが載ったものです。
y_n=x_n^*+\epsilon_y \\
\epsilon_y \sim N(0,R)
これでシミュレーション用のデータが作れるはずです。指定するのは、初期値と制御項です。微分方程式で言えば、状態変数の時間微分に相当する部分の関数です。ノイズはそれぞれ性器乱数を用いて生成できます。
シミュレーション
以上で定式化できているので、あとは実装するだけです。
データの生成
設定するのは
- 離散化の条件としてサンプリングレート $F_s$ [1/sec]とデータ長さ T [sec]: 時刻は$t_n=n*dT$となる。$dT = 1/F_s$
- 初期条件 (初期位置) $x_0$ [m]
- 移動量 $u_n$ [m] for all n in 0
生成してみると、、、
import pandas as pd
import numpy as np
FS, T=4, 100.0# USER SET
x_init = 0.0 # INIITIAL POSITION
Q = 0.1 #Variance of delta position (control term)
R = 1.0 #Variance of measuremnt noise
dt = 1.0 / float(FS)
df = pd.DataFrame([], columns=["ts", "u_true", "x_true", "u", "y", "x", "P", "P_pri", "K"])
df.ts = np.linspace(0.0, T, int(T*FS))
df.u_true = np.sin(2*np.pi / float(T) * df.ts) # USE SETTING
df.x_true = np.cumsum(df.u_true) * dt
df.u = df.u_true + Q * np.random.randn(df.ts.size)
df.y = df.x_true + R * np.random.randn(df.ts.size)
import matplotlib.pyplot as plt
%matplotlib inline
plt.close('all')
import seaborn as sns
sns.set_style("whitegrid")
fig, axes = plt.subplots(2,1, sharex=True)
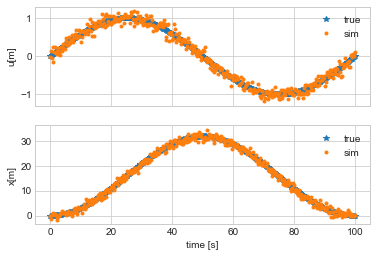
axes[0].plot(df.ts, df.u_true, '*', df.ts, df.u, ".")
axes[0].set_ylabel('u[m]')
axes[0].legend(("true", "sim"))
axes[1].plot(df.ts, df.x_true, '*', df.ts, df.y, ".")
axes[1].legend(("true", "sim"))
axes[1].set_xlabel('time [s]')
axes[1].set_ylabel('x[m]')
Kalman filter simulation
適当な位置の初期値を与えて実行してみると、、、、
#
# Kalman filter
#
x = -100.0
P = 1.0
for idx, row in df.iterrows():
#
# Prediction
#
if idx > 0:
P = P + Q
x = x + df.loc[idx-1,"u"]
#
# filtering
#
# x, P, y = df.x[idx], df.P_pri[idx], df.y[idx]
K = P / (P + R)
x = x + K * (df.y[idx] - x)
P = P * (1.0 - K)
df.loc[idx,"x"], df.loc[idx, "P"], df.loc[idx, "K"] = x, P, K
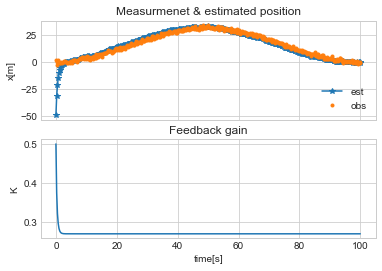
fig, axes = plt.subplots(2,1, sharex=True)
axes[0].plot(df.ts, df.x, '-*', df.ts, df.y, ".")
axes[0].set_ylabel('x[m]')
axes[0].legend(("est", "obs"))
axes[1].plot(df.ts, df.K)
axes[1].set_xlabel('time[s]')
plt.show()
正解位置に寄っていく。