重回帰分析(単回帰分析)
テストデータ
import pandas as pd
df5 = pd.DataFrame({
'x1': [2, 2, 3, 1, 2, 3, 2, 2, 2, 3, 2, 2, 1, 3, 2, 2, 1, 2, 1, 1],
'x2': [2, 2, 3, 2, 2, 1, 2, 3, 2, 3, 2, 1, 3, 2, 2, 1, 1, 3, 2, 1],
'y': [17, 20, 24, 15, 20, 19, 20, 22, 20, 26, 24, 14, 22, 23, 23, 19, 13, 27, 17, 13]})
1. sklern.linear_model.LinearRegression による分析
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
X = df5.drop('y', axis=1)
y = df5['y']
lr = lr.fit(X, y)
1.1. 偏回帰係数と標準化偏回帰係数
元のデータを使って重回帰分析をした結果で,切片は .intercept_,偏回帰係数は .coef_ で求めることができる。
lr.intercept_
7.076023391812857
lr.coef_
array([2.7251462 , 3.75497076])
よくある記事だが,
各変数がどの程度目的変数に影響しているかを確認するには、各変数を正規化 (標準化) し、平均 = 0, 標準偏差 = 1 になるように変換した上で、重回帰分析を行うと偏回帰係数の大小で比較することができるようになります。
などと書いているが,データを正規化して分析をもう一回する必要はない。
1.2. 偏回帰係数を標準化偏回帰係数に変換
標準化したデータで重回帰分析をしたときに得られるのは,標準化偏回帰係数 $b^{*}_i$ である。
元のデータを用いて重回帰分析をして得られる偏回帰係数を $b_i$,$y$ の標準偏差を $S_y$,$X_i$ の標準偏差を $S_{xi}$ とすれば,標準化偏回帰係数は式(1) のようにして求めることができる。
$\hspace{2cm}(1)\hspace{1cm}\displaystyle b_i^{*} = b_i \frac{S_{xi}}{S_y}$
Sy = y.std()
Sy
4.115439478994091
Sxi = X.std(axis=0)
tuple(Sxi)
(0.6863327411532597, 0.7254762501100116)
import numpy as np
tuple(lr.coef_ * (Sxi/Sy)) # 標準化偏回帰係数
(0.45447322703523774, 0.6619322481381958)
疑い深い人は,時間の無駄だが,以下を試せばよい。
更に時間の無駄をいとわない人は,これを証明すればよい。
import scipy.stats as ss
X2 = ss.zscore(X) # 標準化
y2 = ss.zscore(y) # 標準化
lr2 = LinearRegression()
lr2 = lr2.fit(X2, y2)
tuple(lr2.coef_) # 標準化偏回帰係数
(0.45447322703523757, 0.6619322481381954)
ちなみに,定数項は 0 になる。
lr2.intercept_
3.59314957606639e-16
1.3. 標準化偏回帰係数を偏回帰係数に変換
機械学習における重回帰分析の手順書で,
- データを正規化して
- 重回帰分析をして(標準化偏回帰係数を求め)
- 予測値を求めるために
- 標準化偏回帰係数を偏回帰係数にして(予測式を作り)
- 予測式で予測値を求める
ということが記述される。最初にデータを正規化するということの意味をよくわかっていない(誤解した)まま手順書に従うことが多いようだ。
式(1) を $b_i$ について解けば,式(2) が得られる。
$\hspace{2cm}(2)\hspace{1cm}\displaystyle b_i = b_i^{*} \frac{S_y}{S_{xi}}$
つまり,標準化偏回帰係数 $b_i^{*}$ を偏回帰係数 $b_i$ に変換するのだ。
tuple(lr2.coef_ * Sy / Sxi)
(2.72514619883041, 3.7549707602339177)
lr.coef_ と一致している。
定数項 $b_0$ は以下の式で求めることができる。
$\hspace{2cm}b_0 = \bar{y} - \sum b_i * \bar{X_i}$
y.mean() - (lr2.coef_ * Sy / Sxi) @ X.mean(axis=0)
7.076023391812864
これは,元のデータを用いて重回帰分析をしたときの切片(定数項) lr.intercept_ と一致している。
元データで重回帰分析をした結果と,標準化データで重回帰分析をした結果は相互に一次式で変換可能である。
その昔,コンピュータによる計算のコスト(時間的にも金銭的にも)が馬鹿にならない時代には32ビット浮動小数点数を使っていた。そのような場合には計算精度の点から「標準化データで重回帰分析をし,(予測値を求めるために)得られた標準化偏回帰係数を偏回帰係数に変換して...」ということが行われていた。計算アルゴリズムも,「逆行列を求めてどうのこうの」という貧弱なものであった可能性もあるが,現在は64ビット浮動小数点数を使うのが当たり前で,逆行列を使わない計算アルゴリズムが採用されることもあり,もはや標準化データで重回帰分析をしなければならないなんてことはない時代になったのである。
1.4. 決定係数
LinearRegression() で得られる数少ない情報が,決定係数である。これは重相関係数 $R$ の二乗,つまり $R^2$ である。
lr.score(X, y) # R2; coefficient of determination
0.7718952965591936
サンプルサイズ $n$,実測値 $y_i$,予測値 $\hat{y_i}$,$k$ 個の独立変数 $X_{i,j}$,$i=1,2,\dots,n$,$j=1,2,\dots,k$ として
$\hspace{2cm}\displaystyle \hat{y_{i}} = b_{0} + \sum_{j=1}^k b_j\ x_{i,j}$
$\hspace{2cm}\displaystyle S_t = \sum_{i = 1}^{n} (y_i - \bar{y})^2$
$\hspace{2cm}\displaystyle S_e = \sum_{i = 1}^{n} (y_i - \hat{y_i})^2$
$\hspace{2cm}\displaystyle R^2 = 1 - \frac{S_e}{S_t}$
重回帰分析による予測値は .predict() で得られる。
y_hat = lr.predict(X)
Se = sum((y - y_hat)**2)
St = sum((y - y.mean())**2)
R2 = 1-Se/St
(St, Se, R2)
(321.79999999999995, 73.40409356725148, 0.7718952965591936)
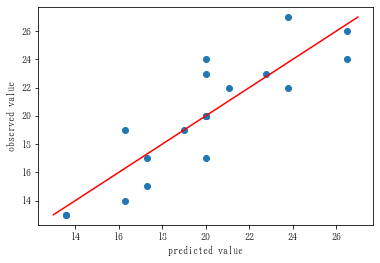
import matplotlib.pyplot as plt
plt.scatter(y_hat, y)
min0 = np.min(np.vstack((y_hat, y)))
max0 = np.max(np.vstack((y_hat, y)))
plt.plot([min0, max0], [min0, max0], color='red')
plt.xlabel('predicted value')
plt.ylabel('observed value')
plt.show()
$R^2$ は 0 〜 1 の値をとり,1 に近いほど(上記散布図において,データ点が原点を通る傾き 1 の直線に近いほど)予測がうまくいっていることを表す。
しかし,説明変数を増やしていけば(たとえどんなに意味のない説明変数でも),$R^2$ はどんどん 1 に近づいていく。
機械学習やさんは,$R^2$ を少しでも上げるために...(惻隠の情で,それ以上言わない)。
$R^2$ が大きくなったのが,説明変数の個数が増えただけなのか,それとも意味のある説明変数が増えたからなのか,そこが知りたい。
そのために,自由度を調整した決定係数 adjusuted R square $R_{adj.}^2$ を使う。
$\hspace{2cm}\displaystyle R_{adj.}^{2} = 1 - \frac{S_e\ /\ (n-p-1)}{S_t\ /\ (n-1)}$
n, p = X.shape
R2adj = 1 - (Se / (n - p - 1)) / (St / (n - 1))
R2adj
0.7450594490955693
$R_{adj.}^2$ が大きくなる限り,追加された独立変数は有効であることを意味する。
$R^2$ の大小だけで一喜一憂するのは意味のないことである。
1.5. 関数を作って,道具箱にしまっておく
$X$, $y$ をデータフレームで与えて,上記の統計情報を返す関数 lm() を定義しておけば,後々まで便利に使うことができる。
from sklearn.linear_model import LinearRegression
import pandas as pd
def lm(X, y):
lr = LinearRegression()
lr = lr.fit(X, y)
b0, b = lr.intercept_, lr.coef_
beta = tuple(b * X.std(axis=0) / y.std())
R2 = lr.score(X, y)
yhat = lr.predict(X)
Se = sum((y - yhat)**2)
St = sum((y - y.mean())**2)
R2adj = 1 - (Se / (n - p - 1)) / (St / (n - 1))
return(dict(b0=b0, b=b, beta=beta, R2=R2, yhat=yhat, R2adj=R2adj))
X = df5.drop('y', axis=1)
y = df5['y']
results = lm(X, y)
results
{'b0': 7.076023391812857,
'b': array([2.7251462 , 3.75497076]),
'beta': (0.45447322703523774, 0.6619322481381958),
'R2': 0.7718952965591936,
'yhat': array([20.03625731, 20.03625731, 26.51637427, 17.31111111, 20.03625731,
19.00643275, 20.03625731, 23.79122807, 20.03625731, 26.51637427,
20.03625731, 16.28128655, 21.06608187, 22.76140351, 20.03625731,
16.28128655, 13.55614035, 23.79122807, 17.31111111, 13.55614035]),
'R2adj': 0.7450594490955693}
2. statsmodels.formula.api を用いて重回帰分析を行う
これは R の lm() や Julia の GLM.lm() と同じように,formula を指定して分析を行うものである。
sklern.linear_model.LinearRegression() を用いる場合よりは,分析の結果としてより多くの情報が得られる。
import pandas as pd
import statsmodels.formula.api as smf
model = smf.ols(formula='y ~ x1 + x2', data=df5)
fitted = model.fit();
2.1. 結果の要約
重回帰分析の結果は .summary() で要約される。
print(fitted.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.772
Model: OLS Adj. R-squared: 0.745
Method: Least Squares F-statistic: 28.76
Date: Fri, 13 May 2022 Prob (F-statistic): 3.50e-06
Time: 22:11:51 Log-Likelihood: -41.381
No. Observations: 20 AIC: 88.76
Df Residuals: 17 BIC: 91.75
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 7.0760 1.777 3.983 0.001 3.328 10.824
x1 2.7251 0.711 3.835 0.001 1.226 4.224
x2 3.7550 0.672 5.585 0.000 2.337 5.173
==============================================================================
Omnibus: 1.132 Durbin-Watson: 1.928
Prob(Omnibus): 0.568 Jarque-Bera (JB): 0.975
Skew: 0.483 Prob(JB): 0.614
Kurtosis: 2.512 Cond. No. 12.3
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
多くの情報を得るために,それぞれメソッドが用意されている。
-
.predict()予測値
print(fitted.predict())
[20.03625731 20.03625731 26.51637427 17.31111111 20.03625731 19.00643275
20.03625731 23.79122807 20.03625731 26.51637427 20.03625731 16.28128655
21.06608187 22.76140351 20.03625731 16.28128655 13.55614035 23.79122807
17.31111111 13.55614035]
-
.cov_params()パラメータ間の共分散行列
print(fitted.cov_params())
Intercept x1 x2
Intercept 3.156351 -0.782775 -0.707023
x1 -0.782775 0.505016 -0.101003
x2 -0.707023 -0.101003 0.451989
-
.params偏回帰係数
print(fitted.params)
Intercept 7.076023
x1 2.725146
x2 3.754971
dtype: float64
-
.bse偏回帰係数の標準誤差 Standard Error of B
print(fitted.bse)
Intercept 1.776612
x1 0.710645
x2 0.672302
dtype: float64
-
.tvalues$H_0:\text{偏回帰係数}=0$ の検定統計量
fitted.tvalues = fitted.params / fitted.bse である
print(fitted.tvalues)
Intercept 3.982875
x1 3.834751
x2 5.585247
dtype: float64
.pvalues
帰無仮説 $H_0:\text{偏回帰係数}=0$ の検定統計量 $t_0$ に対する $p$ 値である。
print(fitted.pvalues)
Intercept 0.000962
x1 0.001327
x2 0.000033
dtype: float64
サンプルサイズ $n$,独立変数の数 $k$ としたとき,自由度 $df = n - k - 1$ の $t$ 分布における両側有意確率($p$ 値)である。
$\hspace{2cm}p = 2\Pr{|t| > |t_0|}$
from scipy.stats import t as tdist
tuple(2 * tdist.sf(fitted.tvalues, 17))
(0.0009622611349048397, 0.001326876714709681, 3.2835740511070946e-05)
偏回帰係数の信頼区間である。信頼度 $100(1-\alpha)%$ のとき, $\alpha$ で指定する(信頼度 = 0.95 で指定するのではないので注意)。
print(fitted.conf_int()) # デフォルトで .conf_int(0.05) すなわち信頼度 = 0.95
0 1
Intercept 3.327699 10.824347
x1 1.225817 4.224476
x2 2.336538 5.173403
-
.t_test()説明変数ごとの結果
説明変数(指定法に注意)ごとの偏回帰係数,標準誤差,$t$ 値,$p$ 値,信頼区間
print(fitted.t_test('x1 = 0'))
Test for Constraints
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
c0 2.7251 0.711 3.835 0.001 1.226 4.224
==============================================================================
print(fitted.t_test('x2 = 0'))
Test for Constraints
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
c0 3.7550 0.672 5.585 0.000 2.337 5.173
==============================================================================
print(fitted.t_test([[1,0,0], [0,1,0], [0,0,1]]))
Test for Constraints
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
c0 7.0760 1.777 3.983 0.001 3.328 10.824
c1 2.7251 0.711 3.835 0.001 1.226 4.224
c2 3.7550 0.672 5.585 0.000 2.337 5.173
==============================================================================
-
.rsquared決定係数
print(fitted.rsquared)
0.7718952965591936
-
.rsquared_adj自由度調整済み決定係数
print(fitted.rsquared_adj)
0.7450594490955693
-
.aic赤池の情報量 AIC Akaike's Information Criteria
print(fitted.aic)
88.76248995183397
-
.bicAIC の発展型である BIC
print(fitted.bic)
91.74968677249595
-
.llf対数尤度 log-likelihood
print(fitted.llf)
-41.381244975916985
2.2. 回帰の分散分析
帰無仮説 $H_0:R^2 = 0$
重相関係数の検定である。平たく言えば,「分析に使用した独立変数で,従属変数は説明できない」ということである。
-
.f_test()回帰の分散分析
回帰の分散分析表の主要部分である。
指定法に注意。
ftest = fitted.f_test([[0,1,0], [0,0,1]])
print(ftest)
<F test: F=28.763589359549435, p=3.5005883503838223e-06, df_denom=17, df_num=2>
ftest = fitted.f_test('x1 = x2 = 0')
print(ftest)
<F test: F=28.76358935954945, p=3.5005883503838113e-06, df_denom=17, df_num=2>
以下で,$F$ 値,$p$ 値,第 1 自由度,第 2 自由度の 4 要素を持つタプルが得られる。
ftest.fvalue, ftest.pvalue, ftest.df_denom, ftest.df_num
(28.76358935954945, 3.5005883503838113e-06, 17.0, 2.0)
$p \lt 0.05$ ゆえ,有意水準 5% で $H_0: R^2 = 0$ という帰無仮説は棄却される($p ≒ 3.5\times 10^{-6}$)。
3. 結論
- 「変数を標準化(正規化)したから正確な解が得られる」ということではない。「標準化しなければ不正確な解しか得られない」ということもない。
- 独立変数をむやみに増やしても,意味のないこともあるんですよということを理解したいものである。