Go to Qiita Advent Calendar 2024 Top
LoginSignup
30
23

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

制御工学Advent Calendar 2023

Day 22
@WandererEng

外乱オブザーバとH∞制御

Last updated at Posted at 2023-12-21

えー いまさら外乱オブザーバ？？
と思った方、少しだけお付き合いください！$H_{\infty}$制御をやりますよ！

はじめに

外乱オブザーバはロボットやモータなどメカトロ制御を中心として、産業界でも広く使われています。歴史的な経緯や利点などについては、以前wcrvtさん がわかりやすく、かつ詳細にまとめています。

今回、外乱オブザーバとロバスト制御の関係性について検証したいと思います。
特に、外乱オブザーバとH∞制御について、下記の論文1をもとにシミュレーションベースで確認します。以下、この論文を美多先生論文1と呼ぶことにします。

この記事では

  • 外乱オブザーバの概要と良いところ
  • H∞制御の概要
  • H∞制御で外乱を抑圧する問題を考えたとき、その結果から外乱オブザーバとよく似た制御器が導かれること
  • それらのMATLAB/Simulinkによるシミュレーション

をお見せします。

各シミュレーションにはMATLAB、Simulink、Control System Toolboxを使っています。
が、Robust Control Toolboxは使っていません。検証に使ったコードは最後の方にまとめて載せておきました。

H∞制御の理論はかなり難解ですが、極力とっつきやすくざっくり内容でまとめました。間違い、ご指摘等ありましたらコメントで教えていただけると助かります。

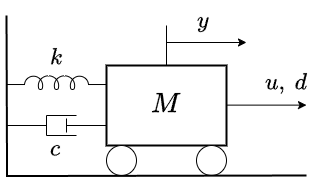
制御対象

本記事では一貫して、下図のバネマスダンパ系を扱います。
smd.png

ここで、質量$M$、バネ定数$k$、粘性係数$c$、変位$y$、制御入力$u$、外力$d$です。運動方程式は下記となります。

\begin{align} 
M \ddot{x} + c \dot{x} + k x = u + d
\end{align}

以下では簡単化のため$M=1$として、$a_0:=k$、$a_1:=c$と置きます。(以降、$k$とか$c$とかは別の意味で使います)

状態方程式は下式となります。この系は$u$と$d$が係数行列$B$を共通でもっていることがわかります。このような系は外乱の推定が出来れば直接$u$で打ち消すことができ、外乱オブザーバと相性がいいです。

\begin{align}
\left( \begin{array}{cc}
\dot{x}_1 \\
\dot{x}_2 
\end{array} \right) &= 
\left( \begin{array}{cc}
 0 & 1  \\ 
-a_0 & -a_1 \\
\end{array} \right) \left( \begin{array}{cc}
x_1 \\
x_2 
\end{array} \right) + \left( \begin{array}{cc}
0 \\
1
\end{array} \right) u + \left( \begin{array}{cc}
0 \\
1
\end{array} \right) d =: A_0 x+b u+b d\\

y &= (1 \quad 0) \left( \begin{array}{cc}
x_1 \\
x_2
\end{array} \right)  =: c x
\end{align}

$u$から$y$までの伝達関数は下式となります。

\begin{align} 
\frac{y(s)}{u(s)} = \frac{1}{s^2 + a_1 s + a_0} =: P(s) 
\end{align}

以下の問題では、外力$d$が1[N]の一定値で印可されることを想定し、その影響を抑制することを考えます。また、具体的な値として$a_0=1$、$a_1=0.5$を与えることにしています。

なお、話題を外乱オブザーバに絞るために、振動の大小自体はあまり気にしないものとします。そちらは別途PD制御などを行うのが普通で、ほぼ上記の$a_0$や$a_1$を変更することに相当します。

本記事の問題設定は最善な$a_0$や$a_1$が設定されたあと、一定値外乱の影響を抑制したい…というような状況だと思ってもらえればと思います。ので、各々の動作確認では、変位$y$の波形がどうなるかはあまり気にしません。あくまで外乱推定の様子がどうなるかを見ていきます。(気になる方はSimulinkモデルを実行して確認してみてください。)

外乱オブザーバについて

詳しいところは、島田明先生の書籍「外乱オブザーバ」2がわかりやすいので参照ください。以下、この本を「外乱オブザーバ本2」と呼ぶことにします。
また、過去記事でまとまっているので、ここでは、あまり触れられることがない視点についてのみ紹介します。

外乱オブザーバは歴史的経緯や、あまり制御理論に精通してなくても使える特徴から、逆に理論に詳しい方ほど毛嫌いされている印象があります。

特に、「外乱オブザーバでロバストな制御を実現します！」というと、たいていの制御理論家さんは眉をひそめます。これは「ロバスト」の意味合いが、理論に詳しい方とそうでない方で違っていたりするためです。理論家は制御対象にパラメータや伝達関数としての不確かさが含まれている状況での安定性や性能保証を議論しますが、そうでない方は外乱を抑圧した、のような意味で使ったりします。理論家からは「それ全然ロバストじゃなくない？普通の制御性能の話では？」となってしまうわけです。

(追記：外乱オブザーバには、外乱を打ち消すだけでなく制御対象をある意味で「ノミナル化」する効果があります3。が、個人的にはその効果を指してロバスト制御だというにはちょっと無理がある気がします)

しかも、ロバスト制御の代名詞H∞制御は、ほぼ外乱オブザーバの手法を包含していて、いわば上位互換であるという内容が冒頭の文献1で示されています。本記事では、この点を確認していきます。

外乱オブザーバの概要

まずは通常の外乱オブザーバについておさらいします。
個人的には、外乱オブザーバ本2でも挙げられているとおり「物理量を推定し、それを相殺するという手法は実装面で容易」という点が特に重要と思っています。

この点あまり強調されることが無いので、念のためシミュレーションで確認してみます。
冒頭で述べたばねマスダンパ系に対し、$\dot{d}=0$の一定値外乱を前提として拡大系を構築すると下式になります。

\begin{align}
\left( \begin{array}{cc}
\dot{x}_1 \\
\dot{x}_2  \\
\dot{d}
\end{array} \right) &= 
\left( \begin{array}{cc}
 0 & 1 & 0 \\ 
-a_0 & -a_1 & 1 \\
0 & 0 & 0
\end{array} \right) \left( \begin{array}{cc}
x_1 \\
x_2 \\
d
\end{array} \right) + \left( \begin{array}{cc}
0 \\
1 \\
0
\end{array} \right) u =: A x + B u\\

y &= (1 \quad 0 \quad 0) \left( \begin{array}{cc}
x_1 \\
x_2 \\
d
\end{array} \right)  =: C x
\end{align}

なお、拡大系の係数行列は

\begin{align}
A &= 
\left( \begin{array}{cc}
 A_0 & b  \\ 
 0 & 0 
\end{array} \right), \quad B= \left( \begin{array}{cc}
b \\
0
\end{array} \right) , \quad C= (c \quad 0) 
\end{align}

となっています。後述のH∞制御でも、似た構造があらわれてくるのでこの構造は覚えておきましょう。

$(C, \ A)$は可観測になるので、この系に対し下記の同一次元オブザーバを構成します。

\begin{align} 
\dot{\hat{x}} = A \hat{x} + B u + L(y - C\hat{x})
\end{align}

ここで、$\hat{x}$は3次元の推定変数、$L$は3次元のオブザーバゲインです。$L$は極配置法などで設計することができます。

これが、もっともシンプルな(状態方程式表現での)同一次元外乱オブザーバです。
オブザーバゲインは後述のH∞制御器との比較をしやすくするため、おおよそですがゲインの大きさがだいたい合うような極に極配置することにしました。

この外乱オブザーバで推定した$\hat{x}$のうち、外乱に相当する要素が推定外乱となります。この推定外乱を符号反転して制御系に印可することで、外乱を相殺することができます。

ちなみに、産業界では位置ではなく速度を計測して、それに対するフィルタをかける形での外乱オブザーバがよく使われます。そちらは伝達関数のかたちで表されることが多いです。外乱オブザーバ本2にて、こうした伝達関数型の外乱オブザーバと、本記事での状態方程式型でのそれとが実質的に同一である点もわかりやすくまとまっています。
(もっと詳しく言うと、最小次元外乱オブザーバにしたとき、伝達関数型のそれと一致します。本記事では同一次元のものを使います)

外乱オブザーバの数値シミュレーション

先ほどの外乱オブザーバをSimulink上で実装し、ステップ外乱の推定の様子を確認してみます。各要素を配置すると下記になります。
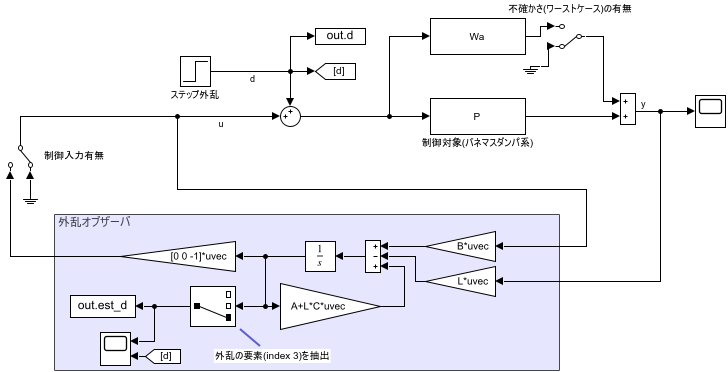
DOB_MSD_poleplace.png

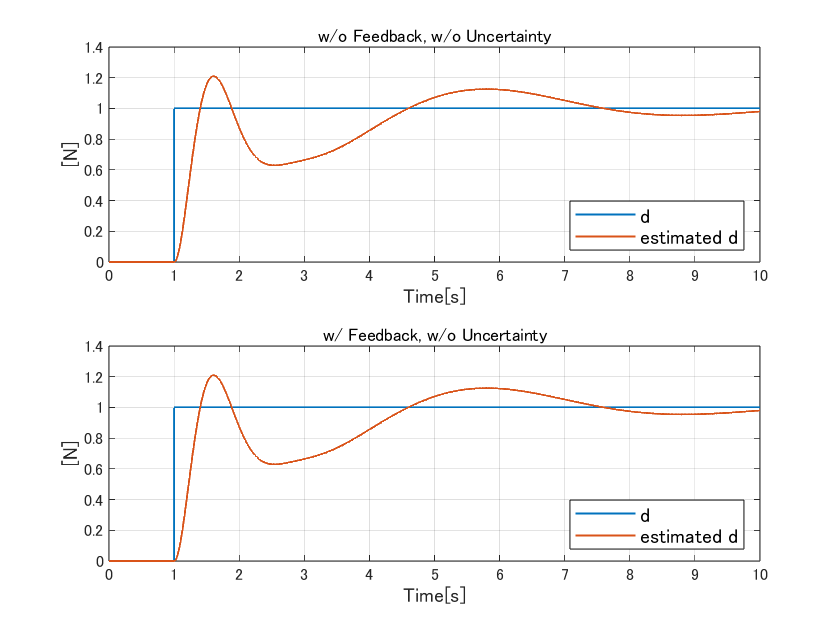
シミュレーション結果は下記です。上のグラフが外乱の推定のみを行った様子、下のグラフが外乱推定値を制御入力として使って外乱を相殺させたときの推定の様子です。
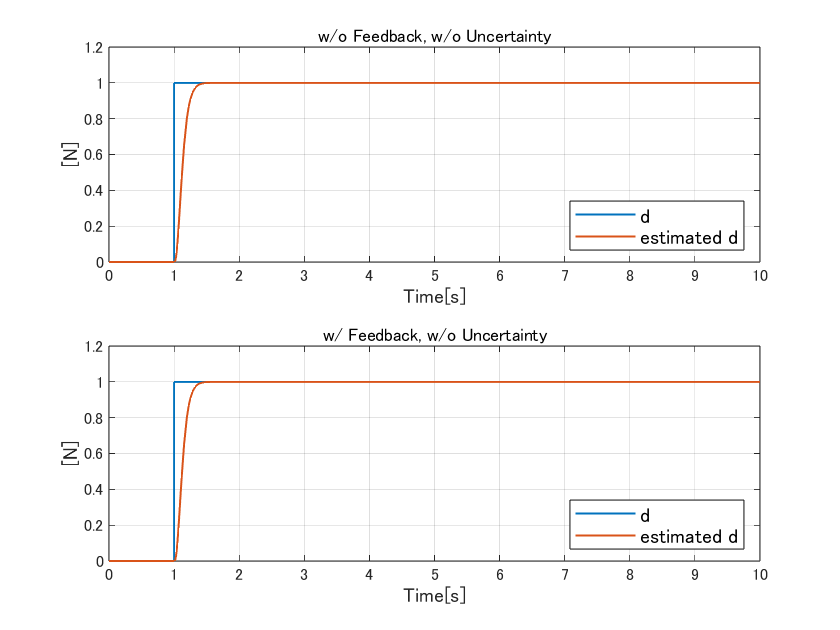
DOB_MSD_poleplace_result1.png

どちらも、一定値外乱に対して速やかに応答しています。また、「外乱の推定のみか、それを使って外乱を相殺する入力として印加するか？」に関わらず同じ応答をします。この点が実用上は結構便利で、

  1. 制御対象をざっくりシステム同定し、推定の様子を机上検証する。
  2. 推定器を実機に実装する。
  3. テスト用の外乱を与え、外乱推定の様子を確認する。
  4. 与えた外乱と推定値が一致していれば、それを符号反転し制御入力として与える。一致していなければ、各係数行列をより詳しくシステム同定しなおす。

というステップでおおよそ上手くいくことが多いです。フィードバック制御器を設計して、実機に実装してみたらなぜか信号が発散して装置が止まった、という経験は多くの方が持っていると思います。外乱オブザーバは、一度「物理量と合ってるか？」の確認ステップがあるため、実装が比較的容易と言えます。

ちなみに、なぜこのような挙動をするかというと、これはもとの制御対象と外乱オブザーバの誤差系を作ったとき、制御入力に関する項$B u$が消えるからです。ここにモデル化誤差がある場合、必ずしも↑のメリットは受けられません。

モデル化誤差ありでの数値シミュレーション

そんな外乱オブザーバですが、やはり大きなモデル化誤差があった場合には上手くいきません。システム同定が上手くできていなかっただけなら上述のステップで確認できるものの、個体によって特性がばらつくような制御対象にはその試行錯誤も無駄に終わります。

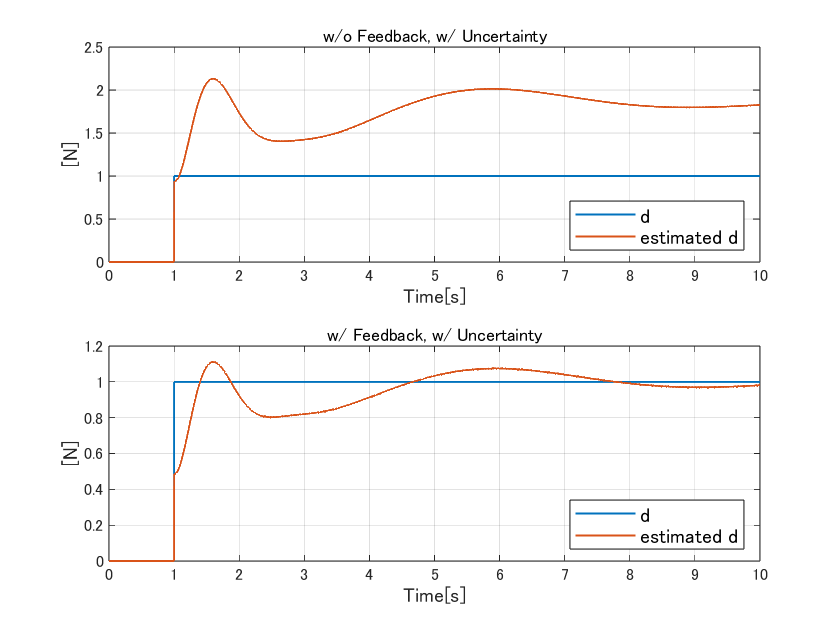
例えば、制御対象$P(s)$が$P(s)+W_a(s)$という別の伝達関数に変わったとしましょう。そのとき、先ほど同様の挙動を確認すると下記のようになります。(なお、具体的な$W_a(s)$の内容はH∞制御のところで説明します。これもH∞制御の検証と条件を揃えるためです。)
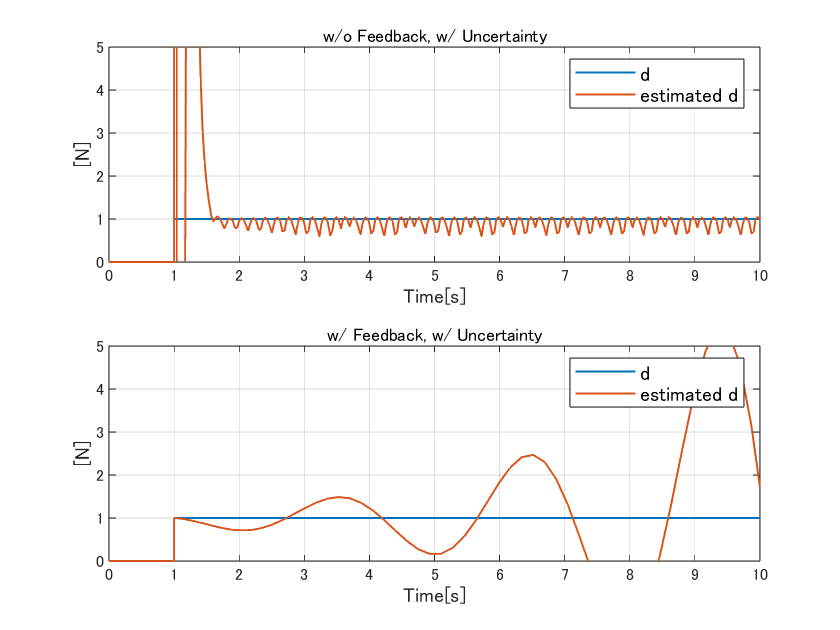
DOB_MSD_poleplace_result2.png

当たり前と言えばそうですが、モデル化誤差がある場合には推定値が正しく得られず、枠外でかなり大きな値になっています(上段の図)。また、それを制御入力として使った場合、まともに動きません(下段の図)。値の推定のみを行ったステップでシステム同定をやり直せば良いこともありますが、個体によってばらつきが多い制御対象には何らかの対策が必要になります。

制御工学的な対策としては多種多様にありますが、例えば下記のようなものが考えられます。

  • オンラインでシステム同定を繰り返したり、制御器の更新を繰り返す適応制御
  • 変わった特性が物理パラメータ(今回の場合はばね定数など)に依存しそれが測定できる場合、パラメータに基づいて制御器を変えるゲインスケジューリング制御
  • 個体のばらつきに対し、安定性を確保しつつ単一の制御器で対処するH∞制御

3つ目の内容が、まさに今回紹介する内容です。
以下、いよいよ本題に入ります。

外乱オブザーバとH∞制御

実は、先ほどの外乱オブザーバの内容が、H∞制御の枠組みで(ある意味)自然に導出することができることが知られています。この点を示したのが、冒頭の文献1です。

H∞制御とは

を簡単に述べるのは非常に難しいのですが、getBack1969さん が大変わかりやすくまとめていただいています。

特に本記事で補足できそうな点としては、

  • 感度関数と相補感度関数って実際何？
  • どうすればロバストな制御器が数値的に求められるの？

などです。

誤解を恐れず非常にざっくりまとめると、H∞制御とは「ロバスト安定性 ＋ 何らかの制御性能」を両立する制御手法だと言えます。「何かしら」の部分が、本記事では「一定値の外乱の影響を抑圧する性能」に相当します。
もう少し補足すると、

  • ロバスト安定性とは、制御対象に不確かさが含まれたとしても、常に安定性を保ち続けること。(より詳しくは、内部安定性だったりも重要ですが…)
  • 何らかの制御性能とは、通常は外乱抑圧性能を指す。目標値への追従性能なども扱える。複数の制御性能を組み合わせて与えることもできるが、それで解が求まるかはやってみないとわからない。H∞制御では、制御対象に不確かさがあった場合の制御性能(ロバスト性能）は保証されない点に注意。

です。ロバスト安定性だけ考えた場合、もともと安定な系だと「何もしない」がロバスト安定性のための最善策となってしまうので、通常は他の性能と両立させることが大事です。

ざっくり言うとロバスト安定性の指標は相補感度関数$T$、制御性能の指標には感度関数$S$と呼ばれる伝達関数が関連していると言えますが、細かいところでごっちゃになって混乱することが多い印象です。これらは後ほどもう少し説明します。

一定値外乱抑圧のためのH∞制御問題

今回、美多先生論文1に条件を寄せることにして、制御対象への不確かさは加法的に、かつ安定な伝達関数$\Delta_a(s)$として表せるものとします。
つまり、制御対象$P(s)$が$P(s)+\Delta_a(s)$と変動する状況を考えます。また、制御対象へ一定値外乱$d$が加わるので、その影響を抑制したい状況です。

これらを踏まえて問題設定すると、下のブロック図のようにインパルス入力$w_1$、$w_2$が印可されたとき、評価用の出力$z$までの2入力1出力の特性$G_{zw}$を扱うことになります。
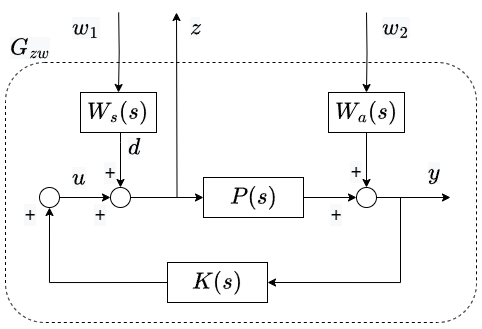
hinf_Gzw.drawio.png
この図の系に対し、

\begin{align} 
 || G_{zw} ||_{\infty} < 1
\end{align}

となる制御器$K(s)$を見つけ出すのが外乱抑圧のためのH∞制御問題となります。ここで、$|| \cdot ||_{\infty}$はH∞ノルムです。

ここで一見わかりづらい点は、4つあります。逆に、H∞制御について知っている方には冗長な内容なので、適宜飛ばしてください。

H∞ノルムって何？

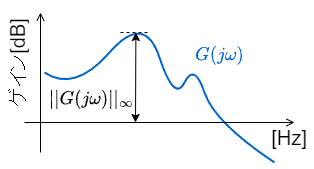
→ 相補感度関数のところで説明するとおり、ロバスト安定性に関わる指標として重要になります。H∞ノルムの概念は単一の伝達関数であれば、下図のように説明されます。伝達関数がピークを取るゲイン値、ということです。
伝達関数が行列となる場合には全周波数帯での特異値の最大値となります。
Hinf_norm.drawio (1).png

与えられた伝達関数行列G_zwに対し、H∞ノルムを極力自力で計算しようとするなら、例えば下記のようなコードになると思います。本来はhinfnorm()で計算すべきですが、計算過程が知りたい場合は参考にしてください。

% 周波数範囲の定義（例：0 から 100 rad/s）
omega = logspace(-1, 2, 500);

% 各周波数での特異値を格納するための配列
singular_values = zeros(1, length(omega));

% 各周波数における特異値の計算
for i = 1:length(omega)
    % 伝達関数行列の周波数応答を計算
    [mag,~,~] = bode(G_zw, omega(i));
    
    % 特異値の計算
    singular_values(i) = max(svd(squeeze(mag)));
end

Hinf_norm = max(singular_values)
$W_a(s)$って何？$\Delta_a(s)$はどこに消えた？

→ $W_a(s)$はH∞ノルムとほぼ同じぐらい大事な概念で、制御対象の不確かさに関する重みを表しています。$\Delta_a(s)$の扱いとともに、ここは次項で念入りに掘り下げましょう。

$W_s(s)$って何？

→ これは比較的わかりやすく、外乱に対する重みを表しています。今回外乱$d$は一定値とみなすので、$W_s(s)=\frac{1}{\gamma}\frac{1}{s}$と考えるだけです($\gamma$の意味は後述しますが、何らかの調整パラメータと思ってもらえればOKです)。ただし、のちのちこの設定によって普通のH∞制御としての解法では解けない問題だと気付かされることになります。これも、$W_a(s)$について述べた後に掘り下げます。

$z$はなぜその位置？

→ 一番直感的には、外乱の影響の抑制度合いを評価するためです。外乱$d$の抑制を制御入力$u$で行うので、その部分を評価しています。おそらくですが、$P(s)$の出力部分を評価してもいいと思います。ただし、各種信号の総合的なつながり方によっては、解けないH∞制御問題になったりするので注意が必要です。

各重み$W_a(s)$、$W_s(s)$は伝達関数のイメージで書いていますが、制御器を求めるにあたって状態方程式表現にします。これら重みを状態方程式として表現し、制御対象に含めて記述しなおしたのが一般化制御対象という概念です。

以下、H∞制御に関する解説が続くので、詳しい方は一般化制御対象の項まで飛ばしてください。

不確かさに関する重みと相補感度関数について

実は先に挙げたブロック図は、$w_1$、$w_2$を除くと下図のような意味合いになっています。逆にいうと、先の図は下図を変形していって導出されたものです。加法的な不確かさを加味した制御対象が右上の部分で、やはり$W_a$に関する部分に説明が必要そうな感じです。
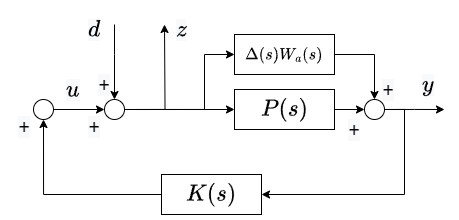
Wa_1.drawio.png
この図では、制御対象に加算される不確かさ$\Delta_a(s)$を$\Delta(s)W_a(s)$と置きなおしています。$\Delta_a(s)$は不確かさの集合を表していて扱いが難しいため、大きさ１以下の不確かさ集合$\Delta(s)$と大きさのスケーリングをする$W_a(s)$にわけました。こうして、$W_a(s)$自体は集合ではなく単一の伝達関数になっていることが重要です。集合的な扱いづらさは$\Delta(s)$に集約されています。

ここで、下図のように端点$\alpha$、$\beta$の部分でブロック図をくくりだすことをします。
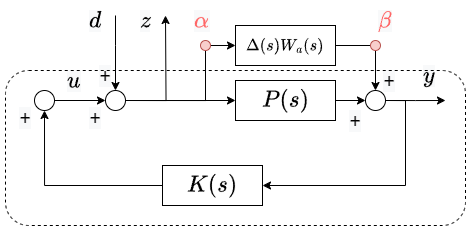
Wa_2.drawio.png

フィードバックループの中身は$T_a(s):=K(s)/(1-P(s)K(s))$と置くことで、下記のようにまとめられます。信号$d$や$z$などは忘れて大丈夫です。
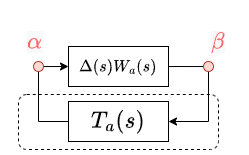
Wa_3.drawio.png

この$T_a(s)$は準相補感度関数と呼ばれます。「準」とか「相補」とかわかりづらいですね。実は、$P(s)(1+\Delta)$のように乗法的な不確かさを考えたうえで上記のくくりだしをすると出てくるのが$T(s)=P(s)K(s)/(1-P(s)K(s))$という関数で、そちらが相補感度関数と呼ばれています。感度関数の話でもう一度取り上げますが、おそらく「もともと、感度関数というものがあった。それと関連があり、かつロバスト安定に関わる関数」という意味で「相補」と呼ばれている気がします。「準」は相補感度関数とよく似ているからついてるんだと思います。

上の図のループで$\Delta(s)W_a(s)$は直列につながっているだけなので、$T_a(s)$の方に寄せてしまいます。
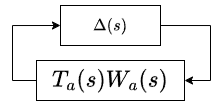
Wa_4.drawio.png

こうして、集合的な$\Delta$と単一の伝達関数$T_a W_a$に分解することができました。これに対して、スモールゲイン定理をあてはめることで、安定性に関する重要な考察が得られます。

【スモールゲイン定理】
上図にて、$\Delta(s)$および$T_a(s) W_a(s)$は安定でプロパな伝達関数とする。このとき$||\Delta(s)|| \leq 1$を満たすすべての$\Delta(s)$について、図の閉ループ系が内部安定となるための必要十分条件は$||T_a(s) W_a(s)||< 1$となることである。

※「∞」記号を省略しています。Qiitaの問題？で文中の数式に「∞」を２回以上続けて入れると表記がおかしくなるみたいなので。

スモールゲイン定理を端的にいうなら「位相条件を無視しゲインにのみ着目した安定性」についての定理です。ゲイン余裕、位相余裕について学んだ方は、「フィードバック系で開ループのゲインが1を下回った時、位相が180度回ってなければ安定」というボード線図での解釈を学んでいると思います。それを集合的な不確かさ$\Delta$に対しても適用するため、「そもそもゲインが1を上回らなければ(位相がどうあろうと)安定」と言ってると解釈ができます。

いくつか補足します。

$||\Delta(s)||_{\infty} \leq 1$を満たす、について

これはそもそも満たされます。不確かさを$\Delta_a(s)=\Delta(s)W_a(s)$として分解したときに、$\Delta(s)$は１以下となるよう、大きさ1をこえる部分は$W_a(s)$に押し込めているからです。

すべての$\Delta$、について

実は大事です。$\Delta$は集合なので一見手ごわい印象ですが「すべての」と言っているのでそれら集合を丸ごと解釈できるわけです。

内部安定性、について 制御対象の出力部分だけでなく、制御器とのつながりの内部的な信号全てに安定性が言えることです。非常に大事な概念ですが、本記事ではあまり触れないことにします。詳しいところは下記のこんとろラボさんの記事が大変わかりやすいので参照ください。 https://controlabo.com/internal-stability/
必要十分条件、について

これも実はすごいです。$||T_a(s) W_a(s)|| < 1$を満たせば安定である、というのはなんとなくそんな気がしますが、逆は一瞬戸惑います。
位相がぐちゃぐちゃな、あらゆる$\Delta(s)$に対して、常に安定性を保つためには$||T_a(s) W_a(s)|| < 1$を満たすしかない、という解釈がいいと思います。

スモールゲイン定理による結果として、$||T_a(s) W_a(s)||_{\infty} < 1$をとにかく満たせばいいことがわかりました。
これは、ブロック図やボード線図のゲイン線図としては下図を意味しています。
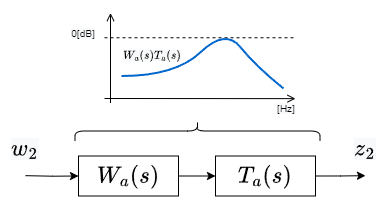
Wa_6.drawio.png

大事な点は、不確かさのくくりだし＆スモールゲイン定理によって、もはや上図はループ状になってない点です。$w_2$というインパルス上の入力、それに対する評価用の出力$z_2$をみたとき、その間にある特性$T_a(s) W_a(s)$がゲインとして１未満(0[dB])であればOK、と言っています。また、スモールゲイン定理を適用したことで、不確かさ集合$\Delta(s)$や、おおもとの$\Delta_a(s)=\Delta(s)W_a(s)$について考える必要がなくなりました。こうして冒頭のH∞制御問題の図には不確かさそのものは除かれ、不確かさの重み$W_a(s)$の記述だけが残ったわけです。

上の図を踏まえると、ようやく元の図に戻ってくることができます。外乱に関する$w_1$は省いてますが、結局下図のようなことが言いたかったわけです。最初に加法的な不確かさを仮定しましたが、もし乗法的な不確かさを仮定した場合には準相補感度関数$T_a(s)=K(s)/(1-P(s)K(s))$を相補感度関数$T(s)=P(s)K(s)/(1-P(s)K(s))$と置き換えるだけで、まったく同じ内容になります。
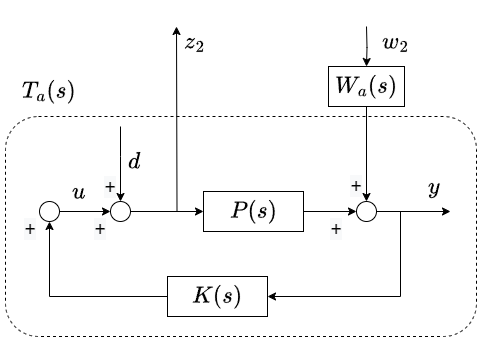
Ta.png

一点補足としては、上述の説明では不確かさを$\Delta_a(s)=\Delta(s)W_a(s)$と分解しました。この説明だと$W_a(s)$を非常に正確に特定する必要がありそうですが、そうではありません。実際には、制御対象のばらつきのゲイン線図をプロットし、それを覆うような$W_a(s)$を求めます。

外乱に対する重みと感度関数について

先に(準)相補感度関数について説明しました。同様に、下図のように$w_1$から$z$までの特性を$W_s(s) S(s)$と表し、$S(s):=1/(1-P(s)K(s))$を感度関数と呼びます。
S.png

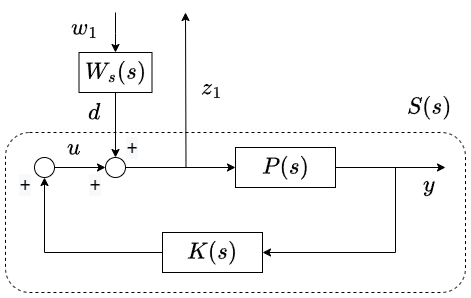
$w_1$はインパルス信号なので、具体的にどのような外乱になるかを$W_s(s)$で指定するイメージです。注意として、この図では制御対象が変動することは考慮していません。感度関数に関しても不確かさを考慮し、不確かさありのもとでも所望の制御性能を満たすことを目指す手法がμ設計と言われる手法です。この性能をロバスト性能(もしくはロバスト制御性能)と呼びますが、本記事ではこのμ設計には深入りしません。

文献によっては、感度関数$S(s)$は

  • 目標位置信号$r$を印可した時の偏差$e=r-y$までの伝達関数
  • 制御対象$P(s)$が変動するときの、閉ループ伝達関数での変動との比

と異なる定義をされますが、いずれも$1/(1-P(s)K(s))$を表しています。歴史的には最後のものが元祖のようです。H∞制御の冒頭の説明で「何らかの制御性能」といったのはこれらをひっくるめようと思ったからです。

また、実はこれらの感度関数は必ずしもH∞ノルムで評価しなくてもいい気がします。個人的には、相補感度関数の方が優先で、そちらがH∞ノルムで評価するのであわせて制御性能もH∞ノルムで評価する…のをH∞制御と呼んでるのではないかと思ってます。(違ったらすみません。)

混合感度問題

$|| G_{zw} ||_{\infty} < 1$を満たす制御器を見つけ出す、と書きましたが具体的に何をやろうとしてるかもう少し書きます。H∞制御問題の冒頭で掲げたブロック図を制御器$K$のところで切断すると、開ループの入出力関係が整理できます。

\begin{align} 
\left(\begin{array}{ccc}
z \\
y
\end{array} \right) =
\left( \begin{array}{ccc}
W_s & 0 & 1 \\
P W_s & W_a & P
\end{array} \right)
\left(
\begin{array}{ccc}
w_1 \\
w_2 \\
u 
\end{array} \right)
\end{align}

これに、$u=K(s)y$を代入して式を整理すると、下式が得られます。

\begin{align} 
z =(S W_s \quad T_a W_a)
\left( \begin{array}{ccc}
w_1 \\
w_2
\end{array} \right)
\end{align}

実は、冒頭で$G_{zw}:=(S W_s \quad T_a W_a)$と置いていたわけです。

この章の冒頭で上げたH∞制御問題は

||(S W_s \quad T_a W_a)||_{\infty} <1

と等価です。これを混合感度問題と呼びます。

なお、$S W_s$のH∞ノルム、$T_a W_a$のH∞ノルムを個別に1未満にすれば良いところをまとめて一つの伝達関数行列として考えるので、保守的な結果になることがあります。
(奇しくも美多先生論文1の説明と逆の流れになりましたが、この記事では雰囲気重視で先に$G_{zw}$を載せることにしました)

余談ですが… こうしたH∞制御の混合感度問題の話、よくよく考えると自分は腑に落ちないところがあります。しばしば感度関数$S$と相補感度関数$T$が$S+T=1$が成り立っていて、制御性能とロバスト安定性には周波数帯に応じたトレードオフがある…という説明がされることが多いです。

たしかにざっくりいいたいことはわかるのですが、本記事でも前述のとおり「準」相補感度関数を扱うので、特に$S+T=1$を意識することはありません。実践ロバスト制御4でも重みの場所を変えたり、修正した混合感度問題を取り上げていて、そこにも$S$とか$T$ではない関数があらわれたりします。また、2つではなく3つ以上の指標に対してH∞ノルムで評価する、ということも可能だと思います。

何が言いたいかというと、あまり「感度」、「相補感度」という言葉に縛られ過ぎない方がいいのではないか、と思った次第です。
このへんが、冒頭の「H∞制御はロバスト安定性＋何らかの制御性能」を満たすような手法だ、と述べたところで言いたかった点です。
(歴史的には感度関数の解析→ロバスト制御と発展してきた経緯があるようですが…。詳しい方のご指摘をお待ちします)

一定値外乱抑圧問題における一般化制御対象

先ほどのブロック図を、状態方程式として記述しなおします。
これまでに2つの重み$W_a$、$W_s$があらわれましたが、これら重みを含めた制御対象を状態方程式として記述したものを一般化制御対象と呼びます。

加法的な不確かさに対する重み$W_a(s)$は伝達関数の形で下記のように表すことにします。

W_a(s) = c_a (sI-A_a)^{-1}b_a + \theta

つまり、状態方程式として実現したときにABCD行列が、$A_a$、$b_a$、$c_a$、$\theta$と対応します。

一般化制御対象というフォーマットに合わせて記述を行うと、閉ループ系$||G_{zw}||の$H∞ノルムを最小化する制御器の係数行列の数値を、(先人たちの知恵によって)簡単に求めることができます。

一般化制御対象は

\begin{align} 
\begin{array}{ccccccc}
\dot{x} & = &  Ax & + & B_1 \omega & + & B_2 u \\
      z & = &  C_1 x &  &  & + & D_{12} u \\
      y & = &  C_2 x & + & D_{21} \omega & & \\
\end{array} 
\end{align}

と表せます。または、これをより簡略的に

G(s) = \left( \begin{array}{c|c:c}
 A & B_1 & B_2 \\
 \hline 
 C_1 & 0 & D_{12}\\
 \hdashline 
 C_2 & D_{21} & 0
\end{array} \right)
=\begin{align} 
 \left( \begin{array}{ccc|cc:c}
 A_0 & b & 0 & 0 & 0 & b \\
 0 & 0 & 0 & 1/\gamma & 0 & 0 \\
 0 & 0 & A_a & 0 & b_a & 0 \\
 \hline 
 0 & 1 & 0 & 0 & 0 & 1 \\
 \hdashline 
 c & 0 & c_a & 0 & \theta & 0 \\
\end{array} \right)
\end{align}

という表記もよく使われます(ドイルの記法)。上記は開ループ系であり、閉ループ系$G_{zw}(s)$とは異なるので注意してください。

先に述べた外乱オブザーバにおける拡大系との違いを説明しておきます。
H∞制御に慣れた人には冗長ですが、もともとの制御対象の状態変数を$x_0$、伝達関数$W_a$の内部状態を$x_a$とすると、この系の状態は$x:=[x_0 \quad d \quad x_a]^{T}$と表せて、下記のようになっています。

\begin{align} 
 \left( \begin{array}{c}
 \dot{x}_0 \\
 \dot{d} \\
 \dot{x}_a \\ 
 \hline 
 z \\
 \hdashline 
 y
\end{array} \right) = 
 \left( \begin{array}{ccc|cc:c}
 A_0 & b & 0 & 0 & 0 & b \\
 0 & 0 & 0 & 1/\gamma & 0 & 0 \\
 0 & 0 & A_a & 0 & b_a & 0 \\
 \hline 
 0 & 1 & 0 & 0 & 0 & 1 \\
 \hdashline 
 c & 0 & c_a & 0 & \theta & 0 \\
\end{array} \right)

 \left( \begin{array}{c}
 x_0 \\
 d \\
 x_a \\
 \hline  
 w_1 \\
 w_2 \\
 \hdashline 
 u
\end{array} \right)
\end{align}

念のため次数についてもまとめておくと、

  • $x_0$はもともとの制御対象の次数(バネマスダンパ系は2)
  • $d$は1次元(高次の外乱を仮定する場合は、その次数分内部状態を持つ)
  • $x_a$は制御対象の不確かさの次数

となります。先の外乱オブザーバに比べ、不確かさに関する分だけ制御対象の内部的な次数が増えたとみなしている、という様子がわかります。

また、外乱オブザーバでは$\dot{d}=0$を仮定して拡大系を作りましたが、H∞制御の拡大系はより入出力関係がわかりやすくなっています。$w_1$というインパルスを入れた結果外乱$d$がどういう信号になるか、が$A$行列の真ん中の要素で決まっています。普通の外乱オブザーバもそうですが、高次の外乱オブザーバを考えたときは係数行列がより複雑な構造になるのだと想像がつきやすくなっています。
なお、$1/\gamma$というのが気になりますがこれは後で説明します。

検証する不確かさの構造

ここで、具体的にどんな不確かさについて検証するか述べます。
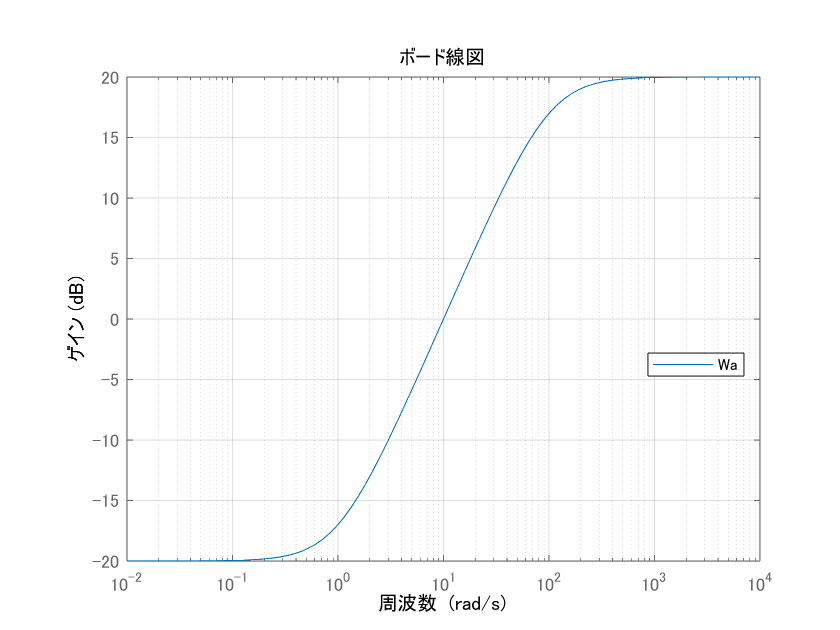
論文1内のものを参考に、下記の伝達関数にしました。高周波に不確かさが大きい、というような意味合いになっています。

W_a(s) = \frac{0.1s+0.1}{0.01s+1}

Wa_Bode.png"

この伝達関数を用いて、$P(s)$がワーストケースとして$P(s)+W_a(s)$と変動することを考えます。

(なお、実際のパラメータ変動を意識した$W_a(s)$を検証したところ、イマイチ微妙な結果に終わりました。そちらは参考までに最後の方に載せておきます)

数値計算による制御器の算出

制御対象が重み関数を含めた一般化制御対象として記述できました。
あとは、MATLABのRobust Control Toolboxのhinfsyn関数でH∞制御器を求めれば終わり…と思いきや、実はそうはいきません！！

一般化制御対象をMATLABで記述してhinfsyn関数を実行すると、下記のようにエラーが出ます。
スクリーンショット 2023-12-11.png

あらためて$A$、$B_2$を眺めると、これらのペアは可制御ではありません($A$、$C_2$は、可観測です)。実はこの点はH∞制御でも外乱オブザーバでも全く同じで、外乱を含めた拡大系を作った際に起きている現象です。
外乱に関する重み$1/s$が不安定な原点極を持つため、標準のH∞制御問題は適用できなくなっています。

ただし逆にいえば、外乱に関する重み$1/s$以外の要素は可制御なので、この場合には拡張H∞制御と呼ばれる枠組みで対処できることが知られています。

拡張H∞制御問題

詳細な適用条件は元文献1を参照ください。ばっさり省略し、結果だけ書きます。
再度一般化制御対象を載せると、下記です。

G(s) =
\begin{align} 
 \left( \begin{array}{ccc|cc:c}
 A_0 & b & 0 & 0 & 0 & b \\
 0 & 0 & 0 & 1/\gamma & 0 & 0 \\
 0 & 0 & A_a & 0 & b_a & 0 \\
 \hline 
 0 & 1 & 0 & 0 & 0 & 1 \\
 \hdashline 
 c & 0 & c_a & 0 & \theta & 0 \\
 
\end{array} \right)
\end{align}

拡張H∞制御を適用するにあたって、いくつかの係数行列を計算しておく必要があります。
それらを下記の通り求めておきます。$\dagger$のダガーマークは疑似逆行列を、$\perp$は直交補空間(内積とったらゼロになるベクトル)を表しています。

\begin{align} 
D_{12} = 1 \quad & \Rightarrow \quad D^{\dagger}_{12}=1, \quad D^{\perp}_{12} = 0 \\
D_{21} = (0 \quad \theta) \quad & \Rightarrow \quad D^{\dagger}_{21}=(0 \quad \theta^{-1})^{T} , \quad D^{\perp}_{21} = (1 \quad 0)^{T} \\
\end{align}

また、下記の行列も求めておきます。

\begin{align} 
E_{12} = D^{T}_{12} D_{12} = 1, \quad E_{21} = D_{21} D^{T}_{21} = \theta^2
\end{align}

これらを準備したうえで、下記のリッカチ方程式の安定化解$X\geq 0$、$Y\geq 0$を求めることで制御器が求まります。

\begin{align} 
X(A-B_2 D^{\dagger}_{12} C_1) + (A-B_2 D^{\dagger}_{12} C_1)^{T}X + X(B_1B^{T}_1 - B_2E^{-1}_{12}B^{T}_2)X + (D^{\perp}_{12}C_1)^{T} D^{\perp}_{12}C_1=0 \\
Y(A-B_1 D^{\dagger}_{21} C_2)^{T} + (A-B_1 D^{\dagger}_{21} C_2)Y + Y(C^{T}_1 C_1 - C^{T}_2 E^{-1}_{21}C_2)Y + B_1 D^{\perp}_{21}(B_1 D^{\perp}_{21})^{T}=0
\end{align}

面食らう式ですが、まずは1つ目の式に着目しましょう。$D^{\perp}_{12}$がゼロなので第4項はゼロになります。つまり、これを満たす$X\geq 0$は$X=0$です。実はこれは$A_0$が安定な場合に限りますが、本記事ではバネマスダンパ系なのでこれでOKです。

このもとで、あとは$Y$さえ求めれば、H∞制御器は下式で得られます(一般的には自由パラメータを含むようですが、自由パラメータ=0とした中心解の内容です)。

\begin{align} 
K(s) = -F_{\infty} (sI-\tilde{A})^{-1} L_{\infty}
\end{align}

ここで、

\begin{align} 
\tilde{A} &:= A + B_2 F_{\infty}+L_{\infty}C_2 \\
F_{\infty} := - D^{\dagger}_{12} C_1, &\quad L_{\infty}:=-B_1D^{\dagger}_{21} - Y C^{T}_2 E^{-1}_{21}
\end{align}

と置いています。

上式の$L_{\infty}$は普通のオブザーバゲインとして機能します。

特に注目すべきは、制御ゲイン$F_{\infty} = - D^{\dagger}_{12} C_1$ の具体的な内容です。

$D^{\dagger}_{12}$は1なので、残るは$C_1$です。$C_1$は評価出力$z$として出力させようとした内部状態…つまり今回の場合では外乱$d$に相当する要素だけを抽出するゲインとなります。さらに、マイナスがかかっているので、外乱の要素を抽出して相殺する制御器を表しています。

おそらく、このへんが一番のポイントです。一定値外乱の抑制問題としてH∞制御器を求めるとき、2つのリッカチ方程式がでてきます。そこで片方のリッカチ方程式の解を$X=0$とした場合、結果はなんと外乱の要素を推定して相殺するような制御器になっている…つまりこれはまさに外乱オブザーバです。外乱オブザーバとの違いは不確かさに関する内部状態が制御器に含まれている点で、まさになんだか上位互換っぽい感じがします。

実際に動作を確認してみるにあたって、あとは2番目のリッカチ方程式について$Y$を求める必要があります。

ただ正直、私はこれを数値的に解くやり方があんまりわかってません。せっかく取り組むからには、他の数値例も汎用的に解けるようにしたいなあと思っていたところ、こちらの文献5でLMI(Linear Matrix Inequality)による数値解法を導出しているのを見つけました。こちらを参考にしつつ今回の問題に適用することにします。

パラメータɤの取り扱い

ここまで、$B_1$行列の$\gamma$について言及を先延ばしにしてきました。具体的な数値解法を述べるには避けられないので、ようやくここで説明しようと思います。

ロバスト安定性に関わる条件は、$||T_a(s) W_a(s)|| < 1$と右辺が1になっています。これは、1未満なら先述のとおり閉ループ系の安定性が言えるからです。
一方、制御性能に関わる条件$||S(s) W_s(s)||<1$は、実は$||S(s) W_s(s)||$が小さければ小さいほど性能が良いと言えます。
美多先生論文1では、この点をふまえて実は$W_s(s)$に調整パラメータ$\gamma$を含ませることにしているのです。

あえて$\gamma$を括りだすと、より最適な制御器を見つけるためには、

\begin{align}
||(S W_s, \quad T_a W_a)||_{\infty} <1 \\
||(S \tilde{W}_s/ \gamma, \quad T_a W_a)||_{\infty} <1
\end{align}

について、できるだけ小さい$\gamma$を見出さないといけません。

この記事では、$\gamma$の含まれていない$\tilde{W}_s$を$W_s$と置き換えて、

||(S W_s, \quad T_a W_a)||_{\infty} < \gamma

の問題をできるだけ小さい$\gamma$について解くことにします。つまり、$B_1$行列に含まれている$\gamma$を外に括りだしたとみなして、$1/\gamma$の要素を$1$に置き換えつつ、上の不等式を満たす最小の$\gamma$を探ることにします。

$T_a W_a$に$\gamma$をかけないと(つまり状態方程式で$b_a$に$1/\gamma$をかけないと)、帳尻合わない気がしますが、H∞ノルムを考えるので等価な問題として扱っていいんでしょうかね…。
あんまりこの点言及してる書籍が見つからなかったので、こう扱っていいものなのかご存知の方は教えてください。

拡張H∞制御問題の数値解法

文献5の内容の結果を一部拝借して、今回の問題に適用したいと思います。

文献5ではより一般的な内容が書かれていて、私の独自解釈で下記を行って適用しました。(ので、あってるかわからないところが多分にあります)

  • 今回は前述のとおり制御ゲインは固定の構造となるので、オブザーバゲインについてのみの不等式を使う
  • LMI可解問題について書かれた内容を、LMI最適化問題となるよう$\gamma$を不等式に含ませる

したがって、本来は文献5内の式(53)～(55)の3つを連立させるところ、(54)を簡略化したものだけ用いています。

結局、下記のLMIを$Y_U\geq0$のもとで解くことでオブザーバゲイン$L$を求めます。$N$はLMIでの変数置き換えによるもので、$N=Y_U L$です。

\begin{align} 
 \left( \begin{array}{cc}
    A^{T} Y_U + Y_U A +C^{T}_{2}N^{T}+NC_{2}+C^{T}_{1}C_{1} & Y_U B_{1} + ND_{21} \\
    B^{T}_{1}Y_U  + D^{T}_{21}N & - \gamma^2 I
\end{array} \right) < 0 
\end{align}

この不等式をぎりぎり満たすように$\gamma$を小さくし、$Y_U$と$N$を求めます。それらをもとに、オブザーバゲイン$L$は下式で求められます。

\begin{align} 
 L = Y^{-1}_U N
\end{align}

LMIについて本記事で説明する余裕はありませんが、川田昌克先生の文献6が非常に参考になります。本記事もSeDuMi/YALMIPを使用してLMIを解くことにするので、それらのインストール方法などは川田先生の下記ページを参考にしてください。

実際にオブザーバゲインをLMIで求めるMATLABコードについて補足します。文献5に則ってより一般的な拡張H∞制御問題を解くLMIをベースにしているので、余計な代入・演算がそのままになってます。特に今回下記の部分はほぼ左辺＝右辺となっていて、実質的にはやらなくてよかったりします。

U0 = zeros(n,n);
U1 = eye(n);
U1_dag = pinv(U1);
A_U = U1*A*U1_dag;
C1_U = C1*U1_dag;
C2_U = C2*U1_dag;
B1_U = U1*B1;
U_L = zeros(2,1);

下記がLMIを解いてオブザーバゲインを求めるコードです。「2」は↑のU_Lの次元(もっというとB1_U)の次元からくる数字です。最初のパス設定は、SeDuMiとYALMIPをダウンロード＆解凍したフォルダへ指定する必要があります。
SeDuMiはこちら 、YALMIPはこちらを参照の上、各々ダウンロードして下さい。

YALMIPでは「solvesdp(行列不等式のリスト、最小化する変数)」の形で記述すると、指定した変数を最小化するようなLMIの解を求めてくれます。求めた解から$L = Y^{-1}_U N$を用いてオブザーバゲインが算出されます。変数epはYALMIPが半正定/半負定の行列不等式しかサポートしていないために使用しており、この点も川田先生のページを参考にしました。

% SDPソルバとLMIパーサのパスの設定
addpath(genpath('~sedumi-masterへのパス~'))
addpath(genpath('~YALMIP-masterへのパス~'))

Y_U=sdpvar(n,n,'sy');
N=sdpvar(n,1); % N=Y_U*U_1*L;
gamma = sdpvar(1); % 実際にはこの変数はガンマの2乗を表す

% -------------------
LMI=[]; % LMI initialized

ep = 1e-6;
LMI=[LMI, Y_U>=ep*eye(n)];

LMI2 = [A_U'*Y_U+Y_U*A_U+C2_U'*N'+N*C2_U+C1_U'*C1_U   Y_U*B1_U+N*D21;
    B1_U'*Y_U+D21'*N'  -eye(2)*gamma];
LMI=[LMI, LMI2<=-ep*eye(n+2)];

% -------------------
sol=solvesdp(LMI,gamma);

if sol.problem~=1;
	Y_U_a = double(Y_U)
	N_a = double(N)
    gamma_a = double(gamma)
else
    disp(sol.info)
end
Y = U1_dag * inv(Y_U_a) * U1_dag';
L = inv(U1) * inv(Y_U_a)*N_a

求めたオブザーバゲインから閉ループ系を構成して$T_a(s)$を求めて、$W_a(s)$とのゲイン線図の大小関係を確認すると下記になります。
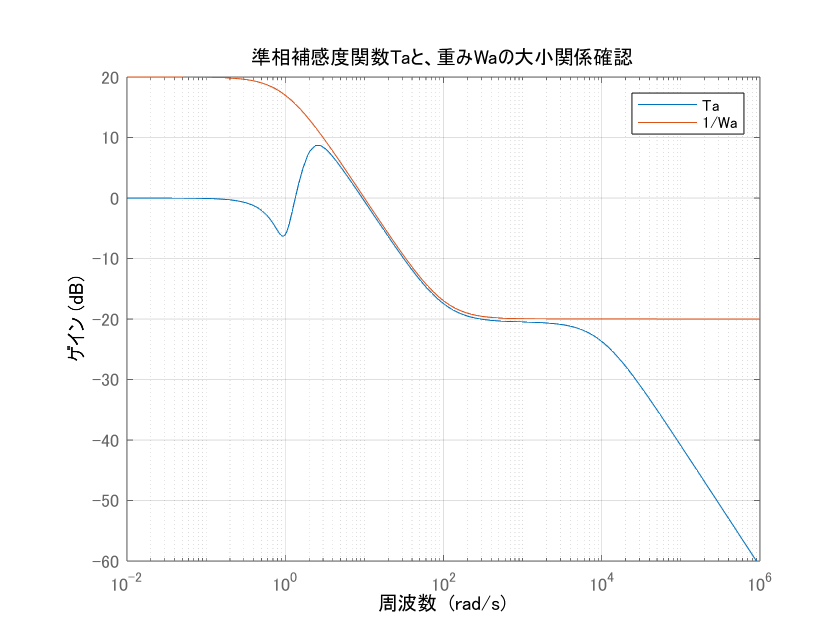
DOB_MSD_LMI_bode.png
結果、無事にH∞制御の書籍でよく見るような図になりました。

この図から$T_a(s)$が$1/W_a(s)$を全帯域で下回っていることが確認できます。すなわち$|T_a(s) W_a(s)| < 1$を満たしている、つまり制御対象が$P(s)$から$P(s)+W_a(s)$と変動しても安定性が確保されていることがいえます。

以下、Simulinkでこの制御器をシミュレーションしてみます。

数値シミュレーション

以上で求めた(ほぼ外乱オブザーバと言える)H∞制御器を、Simulinkで実装したものが下記です。
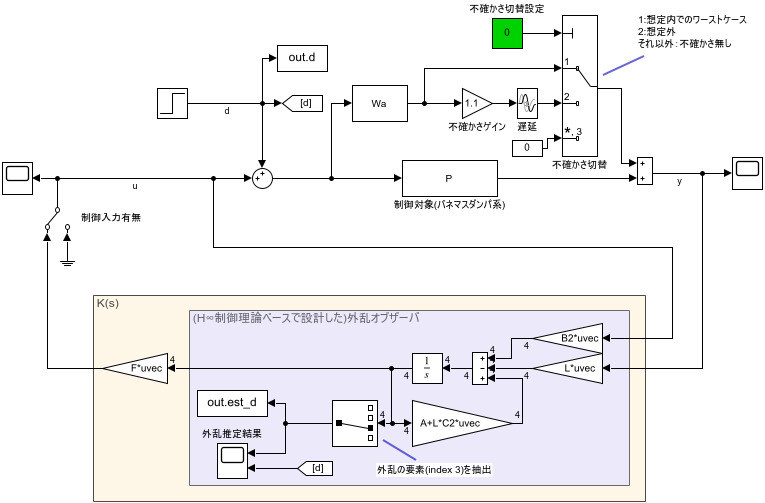
DOB_MSD_LMI.png

制御器の構造自体はほぼ全く同じです。違うのは、想定した不確かさの内部状態の次数分、制御器(≒観測器)の次数が増えています。図中の$F$は、前述のとおり推定外乱の要素だけ-1で、あとはゼロのベクトルです(中央下部のSelectorブロックとやっていることは同じです)。

右上に色々くっついているのは不確かさを与えたときの検証用ブロックで、H∞制御器とは関係ありません。

シミュレーション条件は3パターン試してみます。最初の2パターンは普通の外乱オブザーバで試した内容と同じです。

  • ノミナルでの外乱推定の様子
  • 制御対象が$P(s)$が$P(s)+W_a(s)$と変化した場合の外乱推定の様子
  • 制御対象が$P(s)$が$P(s)+W_a(s)$を超えて変化した場合の外乱推定の様子

3つ目は、設計したH∞制御器がホントに最適だったのかを検証するものです。
LMIによって$||T_a(s)W_a(s)||<1$を満たすようなぎりぎりの$\gamma$を求めているなら、$W_a(s)$からさらに少しだけ制御対象が変化したときに制御系として発散するはずです。この点を事前確認するコードが下記です。

margin(1.1*Ta*Wa) % …ゲイン余裕&位相余裕はないが、ゲイン1.1倍で即破綻するわけでは無さそう。

delays = tf(1,1,'inputDelay',0.001); % Ta*Waが位相線図的にまだ余裕ありそうなので、適当なディレイを挿入
bode(Ta*Wa,1.1*Ta*Wa*delays,{0.1,10000})
title('想定内ワーストケースでの不確かさ込み閉ループと、想定を超えて与えた例')
legend('Ta*Wa','1.1*Ta*Wa*delay','Location','southwest')

margin()関数で確認すると、$W_a(s)$を1.1倍すると$T_a(s)W_a(s)$のゲインが0[dB]を超えるようです。
ただ、これだけだと制御系が発散することはなかったので、位相的にも無理やりディレイを0.001[s]入れて遅らせることにしました。その様子が下記のボード線図です。ので、Simulinkモデルでも同様にゲイン1.1倍、ディレイ0.001[s]を想定外の不確かさとして与えることにしました。

ClosedLoop_OverLimit.png

なお、ゲインだけだと100倍しても1000倍しても発散することはありませんでした。
この点あんまりよくわかりませんが、位相線図を見るとそんなに180°からの変化量が無いためかな、とか思いました。

逆に、ディレイのみをどれだけ遅くしても制御系は発散しません。こちらはスモールゲイン定理の意図通りで、位相としてどれだけ遅れがあっても、ループでつないだときのゲインが1未満を保っているため発散することがないからです。

シミュレーション結果

まずは制御対象の不確かさが無い場合の動作が下記です。
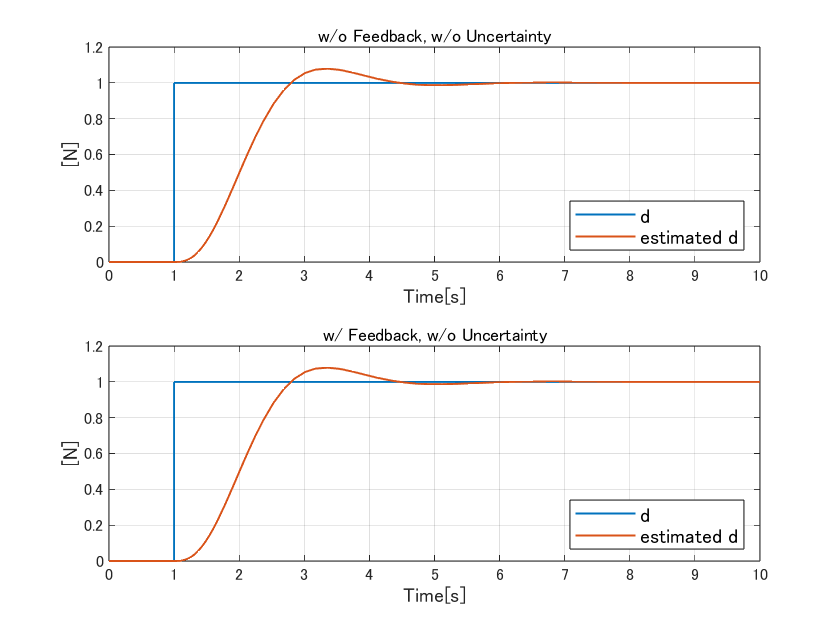
DOB_MSD_LMI_result1.png
どちらも、極配置指定で設計した外乱オブザーバに比べて応答が遅く、オーバーシュートはするものの機能自体はまったく外乱オブザーバと同じになりました。制御入力の印可有無で応答が変わることもありません。

次に、想定した不確かさとしてはワーストケースの、$P(s)$が$P(s)+W_a(s)$と変化した場合が下記です。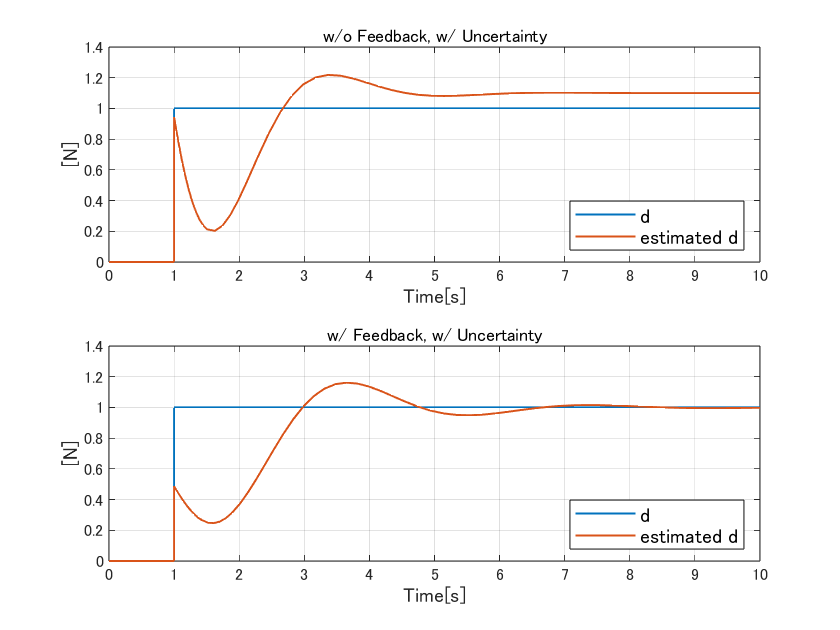DOB_MSD_LMI_result2.png
この条件では通常の外乱オブザーバは発散してしまいましたが、H∞制御ベースのものはあらかじめ不確かさを考慮して設計しているので発散することはありません。制御入力として印可せずに推定だけした上側の図は定常偏差が残ってますが、これはそういうものです。あくまで今回は外乱を抑圧するH∞制御器を考えたので、推定だけ行った場合の偏差がゼロになることは保証していないためです。推定だけだと偏差が残るものの、制御入力として印可した場合にはちゃんと安定的に動作することが確認できました。

最後に、設計したH∞制御器にて、想定した以上の不確かさを与えた場合が下記です。
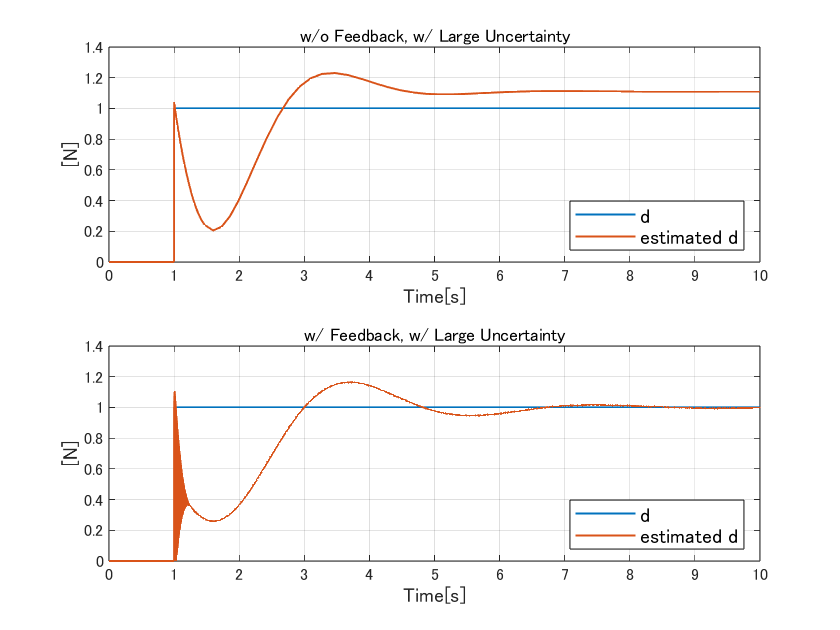
DOB_MSD_LMI_result3.png
ステップ状の外乱が入った瞬間、応答がかなり発振的になっています。

この結果はかなりうれしいです。無事、「設計したH∞制御器は不確かさの事前想定に対して最善を尽くした」と言えそうだからです。そう考えると、1つ目のグラフの応答が遅いのも納得がいきます。3つ目の条件でぎりぎり耐えるか耐えないか…ぐらいのロバスト安定性を保つためには、ノミナル性能としては妥協せざるを得ない様子が実感としてわかりました。

シミュレーション結果の総まとめ

以上で、H∞制御では制御対象の不確かさを考慮した外乱推定、そしてその抑制が行えることがわかりました。特に、想定した不確かさぎりぎりまで動く、ある意味最適な制御器になっていることもおおよそ確認できました。

ただ、明らかに応答性が遅いのも事実です。この遅さのわりに標準のH∞制御で扱えない問題に足を突っ込むことになるので、設計の技術ハードルも高めな印象です。

結局、制御系設計は場合によりけりで、コストと時間のバランスが大事です。個人的な所感では、

  • 簡単に設計でき、ある程度の応答性が欲しい
  • 制御系のパラメータチューニングは人手で何度か試せばOK
  • 制御対象のばらつきをそこまで気にしない(納入品・製造組立の管理で対処できる、とか)

などなどのときには普通の極配置などでの外乱オブザーバが向いていて、

  • 実機実験は一度きりのトライで失敗できないが、事前検証は十分時間が取れる
  • そもそも制御対象が不安定系
  • パラメータチューニングを試行錯誤で繰り返すことができない
  • 制御対象のばらつきを無視できない(納入品・製造組立の管理コストが膨大、とか)

などなどのときには、H∞制御的な不確かさへの事前準備をするのが良いと思いました。

設定するH∞制御問題や、リッカチ方程式の解の選び方次第では、「外乱という物理量を推定して相殺する」という構造自体は実は外乱オブザーバと同じになる、というのが今回わかってよかったです。

その他の検証

実は上手くいってない結果、イマイチだった結果を載せておきます。

美多先生論文が完全には再現できていないところ

実は本記事のコードでは、美多先生論文1での例題3にて、$W_{a1}(s)=0.1$と与えた結果が再現できてはいないです。($W_{a2}(s)$、$W_{a3}(s)$はそれらしいゲイン線図が得られました)
下図のとおり、本来H∞制御器を実装した結果の$T_a(s)$のゲインピークは20[dB]ぐらいになるはずのところ、10[dB]になってしまいました。
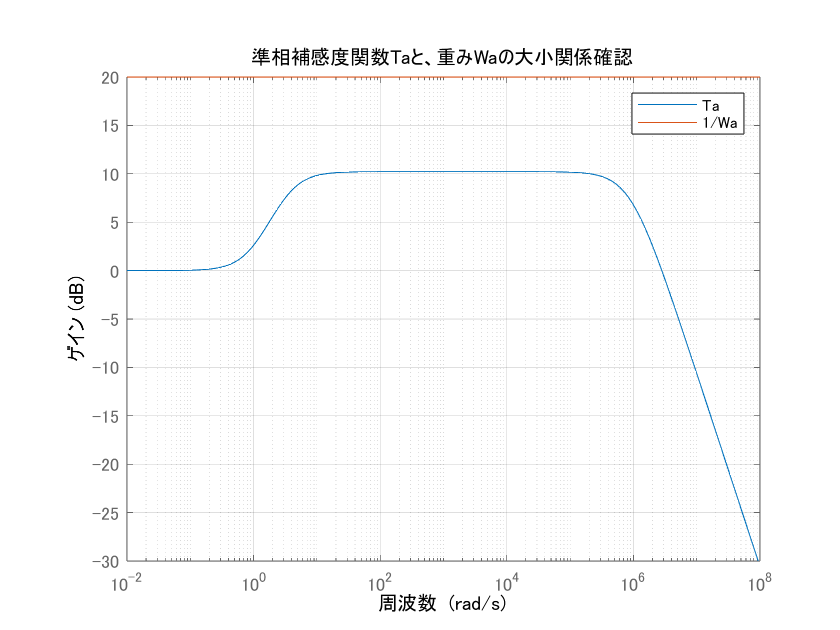
Bode_example2and3_Wa1.png
本来20→実際10[dB]の差異なのでどこかしらが平方根になっているのだと思い、一番怪しい$\gamma$まわりを確認してみましたがよくわかりませんでした。
本記事のコードを使用する際にはご注意ください。

実際のパラメータ変動を意識した不確かさWa(s)を与えた場合の検証

本記事では、バネマスダンパ系に載る不確かさとして、上述のとおりの$W_{a}(s)$を用いました。ただ、これはちょっと現実的な不確かさでもない気がします。

より実際のパラメータ変動を意識して、バネ定数や粘性係数が5%程度変わる前提で、Robust Control Toolboxのucover()を用いて重み関数$W_a(s)$を求めました。
ucover()で得られた結果から、不確かさに関する記述のみ下記のように変更することにしました。

Aa = [-16.05  -15.94;16.08   15.91];
Ba = [1.52;-1.52];
Ca = [1.747  1.73]*5;
theta = 0.00578*5;

これをゲイン線図として描画すると下図になります。
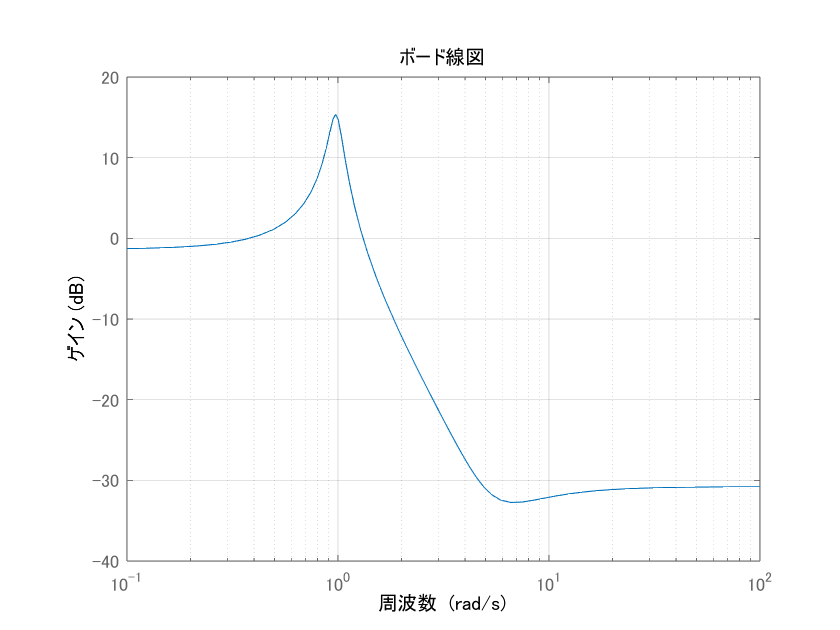
Wa_Ptn2_Bode.png
共進周波数付近でより不確かさが大きく、高周波にもそこそこの不確かさがある、という直感的にも納得いくものとなっています。

この不確かさに対して、H∞制御器を設計しなおしました。得られた制御器から$T_a(s)$を求めて不確かさとの大小関係を比較すると、やはり下図のとおり意図通りの結果になりました。
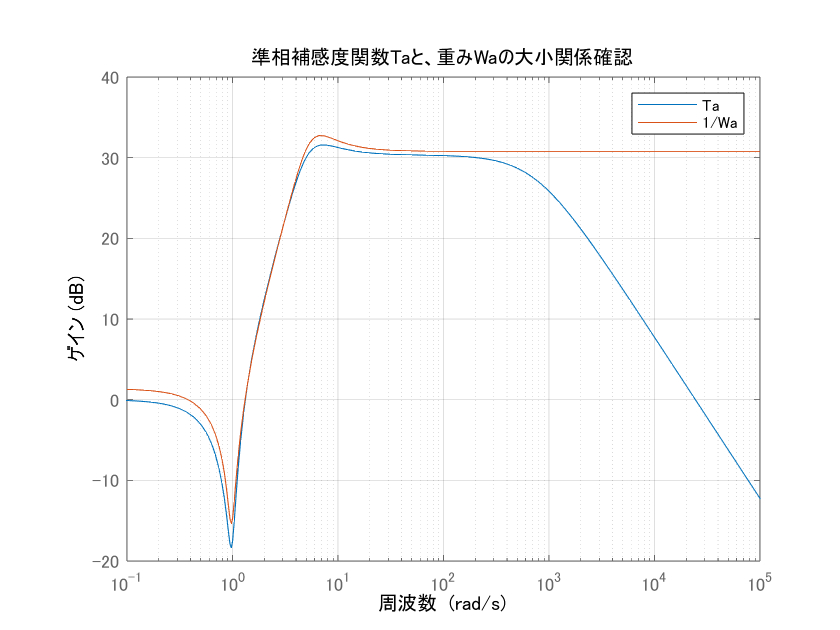
DOB_MSD_LMI_bode_Ptn2.png
得られたH∞制御器に対し、動作確認をしてみました。シミュレーション条件は下記の2つです。

  • ノミナルでの外乱推定の様子
  • 制御対象が$P(s)$が$P(s)+W_a(s)$と変化した場合の外乱推定の様子

それぞれ、下図のようにおおむね意図通りの結果になりました。

DOB_MSD_LMI_result1_Ptn2.png

DOB_MSD_LMI_result2_Ptn2.png

ここまでは良いのですが、実はこの不確かさのもと、普通の外乱オブザーバも特に発散することなく動きます。
下図は、実際のパラメータ変動を意識した不確かさを与えたときの、外乱オブザーバの挙動です。極の位置などは変えず、Simulinkモデル上で制御対象の不確かさだけ変わっている状況です。
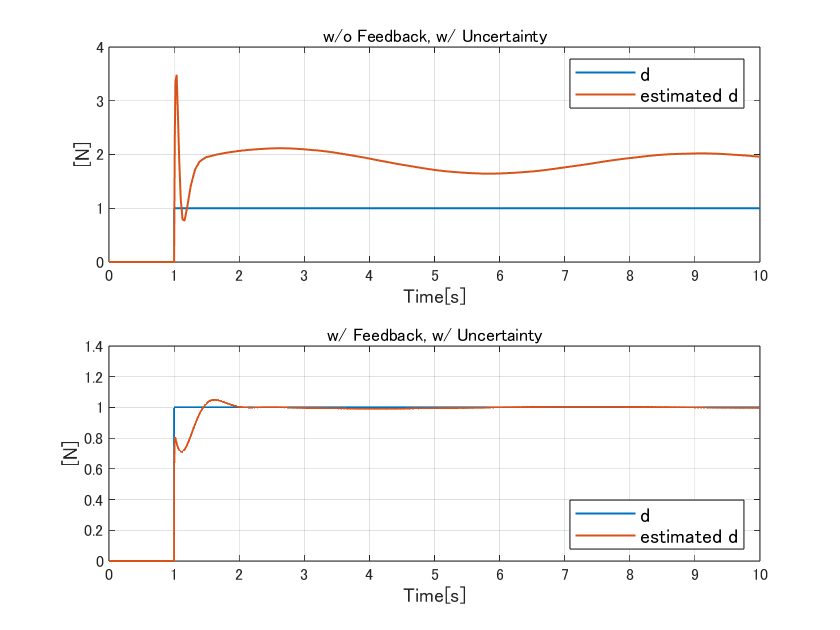
DOB_MSD_poleplace_Ptn2.png

なんと、不確かさありでも応答性が良く、H∞制御器を使う意味とは？？となってしまいそうです。

この点もう少し確認するため、外乱オブザーバによる制御器$K(s)$を求めてみます。
美多先生論文1には外乱オブザーバの制御器$K(s)$の計算式が書いてありますが、そちらは最小次元オブザーバなので本記事とはちょっと違います。
わざわざ計算式を求めるのも辛かったので、Simulink Control Designの機能：モデル線形化器(使い方はこちら)を使ってサクッと求めることにしました。

モデル線形化器で求めた$K(s)$から準相補感度関数$T_a(s) = K/(1-PK)$を求めて、不確かさパターン1(最初に検証したもの)、不確かさパターン2(実際のパラメータ変動を意識したもの)との大小関係をゲイン線図で確認すると、下図です。

Bode_poleplace_Wa1and2.png

上の図をみると、ある程度結果に納得がいきます。青線の$T_a(s)$は(不確かさを除いた)制御対象と制御器$K(s)$からなるので、不確かさに関わらず固定です。最初に与えた不確かさ(赤線)だと、高周波で明らかに$|T_a(s)|>|1/W_a(s)|$となってしまうので$|T_a(s) W_a(s)|<1$を満たさず発散します。一方、実際のパラメータ変動を意識した不確かさ(黄線)は$T_a(s)$と傾向が似たゲイン線図になっていて、やや怪しい箇所はあるものの即座に発散したりしなさそうな様子です。

この結果から、「普通の外乱オブザーバも、実際のパラメータ変動を意識した状況に対するロバスト安定性はそこそこあるのでは？？」と言えそうです(ロバスト安定性に「そこそこある」という表現が通用するかは微妙ですが)。個人的には、実はこのへんも外乱オブザーバが使われている裏事情だったりするのかな、とか思いました。

本記事の裏の結論としては、「H∞制御器使うかどうかは別として、不確かさと相補感度関数のゲイン線図上での大小関係は確認するといいよ」ってとこですかね。H∞制御器を使うことを前提に設計すると技術ハードルが高い印象ですが、もともとある制御器のロバスト安定性に不安がある場合には、この点だけでもみておくと安心感は違うような気がしました。

使ったMATLABコード、Simulinkモデル

MATLAB 2020bです。文献1と文献5の後追い検証に使ったコードはfollowupフォルダに置きました。

おわりに

外乱オブザーバとH∞制御の関係性について検証しました。H∞制御は難解ですが、この記事が誰かのお役に立てたら幸いです。

ちなみに、これを書くにあたって美多先生のH∞制御本7を眺めてみたところ、下記の記述がありました。外乱オブザーバ本2の島田先生と美多先生は昔からつながりがあったようです。この記事を書こうと思ったきっかけは外乱オブザーバ本2なので、個人的に「うおお！そこがつながるのか…！」と熱い気持ちになりました。

Hinf_mita.png

  1. 「H∞制御と外乱オブザーバの理論」, 美多 勉,平田 光男,村田 健一, 電気学会論文誌. C, 1995, https://www.jstage.jst.go.jp/article/ieejeiss1987/115/8/115_8_1002/_pdf/-char/ja ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7 ↩8 ↩9 ↩10 ↩11 ↩12

  2. 「計測・制御セレクションシリーズ2 外乱オブザーバ」, 島田 明, コロナ社, 2021, https://www.coronasha.co.jp/np/isbn/9784339033823/ ↩ ↩2 ↩3 ↩4 ↩5 ↩6

  3. 「現場で役立つ制御工学の基本」, 涌井 伸二，橋本 誠司，高梨 宏之，中村 幸紀　共著, コロナ社, 2012 ↩

  4. 「システム制御工学シリーズ11 実践ロバスト制御」平田 光男, コロナ社, 2017, https://www.coronasha.co.jp/np/isbn/9784339033113/ ↩

  5. 「リッカチ不等式を用いた拡張H∞制御問題の可解条件の導出」, 平田 光男, 佐藤 隆之, 劉 康志, 美多 勉, 計測自動制御学会論文集, 1998,
    https://www.jstage.jst.go.jp/article/sicetr1965/34/7/34_7_741/_article/-char/ja/ ↩ ↩2 ↩3 ↩4 ↩5 ↩6

  6. 「LMIに基づく制御系解析・設計(<特集>制御系解析・設計における数値計算/数式処理ソフトウェアの活用)」, 川田 昌克, 蛯原 義雄, システム/制御/情報, 2011,
    https://www.jstage.jst.go.jp/article/isciesci/55/5/55_KJ00007227375/_pdf/-char/ja ↩

  7. 「H∞制御」, 美多 勉, 昭晃堂, 1994 ↩

30
23
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
30
23

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?