オーバーシュートとゼロ点～2次の実極・実ゼロ点を中心に～

はじめに

先日、↓の記事を書きました。本記事はその続編的な位置づけです。

前回についておさらいすると、

• ボード線図からオーバーシュートの有無を見分けるのは、難しい場合もある
• ノッチフィルタの場合、極が複素成分を持つかどうかでオーバーシュート有無が決まる

などを紹介しました。今回は、ゼロ点とオーバーシュートの関係性について紹介していきます。ただし、前回記事で述べた通り一般的な内容を言うのは難しそうなので、かなり範囲を絞った内容とします。

具体的には、本記事では2次の実極・実ゼロ点のみをもつ伝達関数を中心に話をします。途中でやや一般的なゼロ点の話にも触れますが、不安定ゼロ点などについてはあまり触れません。不安定ゼロ点を含む伝達関数はアンダーシュートと言われる特徴的な挙動があらわれたりで興味深いですが、それらについては多数文献があるのでそちらを参照ください。本記事が、伝達関数のオーバーシュートってどうやって見分けるの？ゼロ点って結局何なの？の理解の助けになれば幸いです。

内容に間違い等あったらコメントくださると助かります。

オーバーシュートの定義

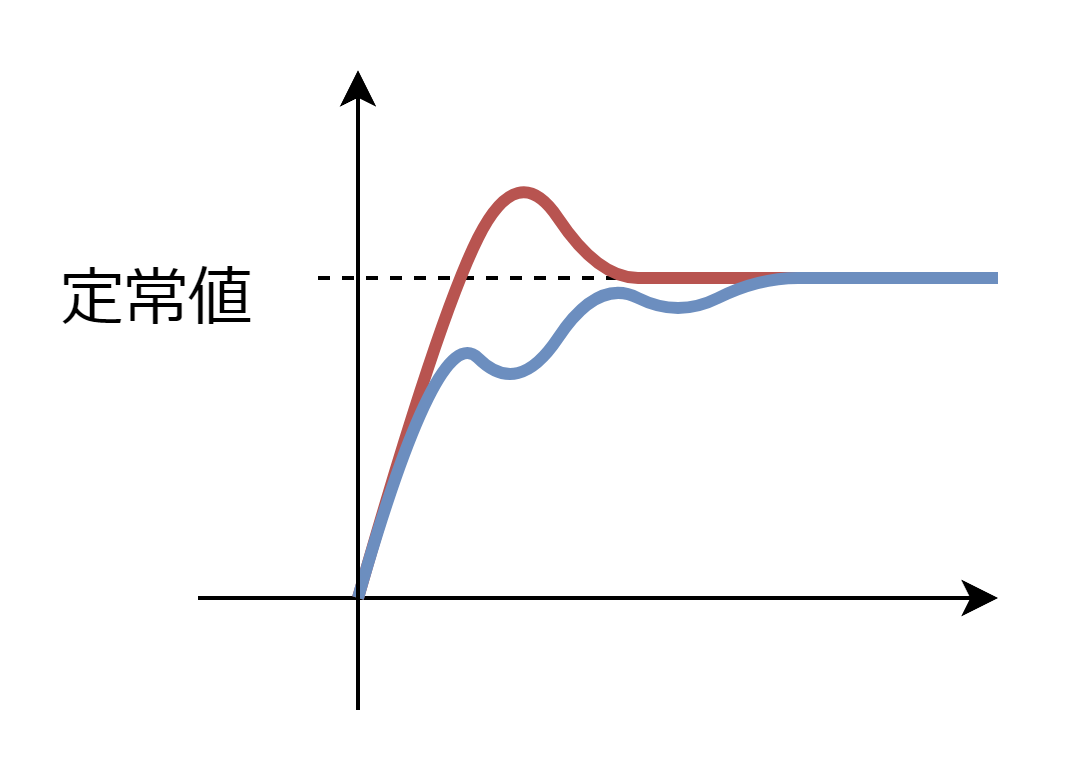
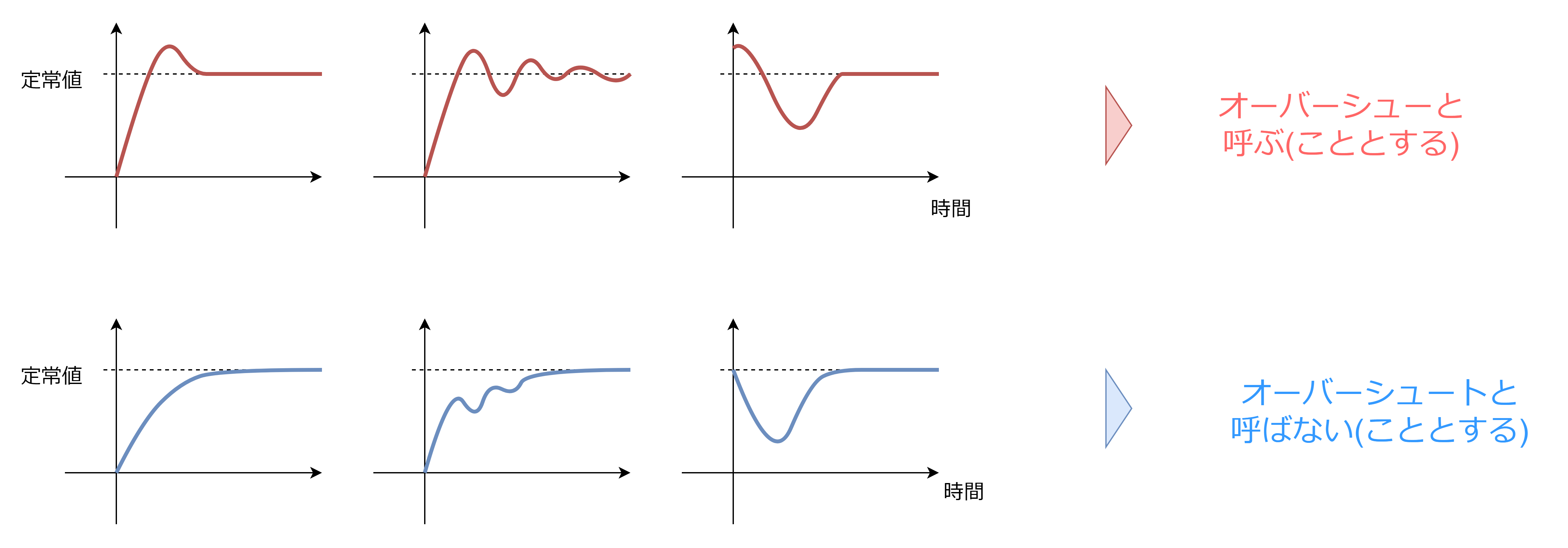
本記事でいうオーバーシュートについて再度明確にしておきます。前回記事と同様、伝達関数のステップ応答について、定常値を上回る瞬間が一瞬でもあったらオーバーシュートと呼ぶことにします。

イメージ図は下記ですが、前回から少し追加があります。一番右上の例は前回なかったですが、今回明記することにしました。今回扱う伝達関数は分母分子の次数が同じ(バイプロパという)ものを考えるため、初期値が発生します。初期値の時点で定常値を超えているものもオーバーシュートと呼ぶことにします。

伝達関数がゼロ点を持たない(極のみの)場合のオーバーシュート有無

前回例示したので省略します。おおまかには、虚軸に近い方の極が複素極ではなく、実極になっているとオーバーシュートしないととらえてよさそうです。もう少し詳しくは、(できたら)後日記事にしようかと思います。

伝達関数が極ゼロを含む場合のオーバーシュート

ゼロ点を含む伝達関数を考慮しだすと、話が複雑になってきます。
まず、文献¹を引用して、ゼロ点を持つ伝達関数のオーバーシュートに関わる性質を紹介します。

一例として、最小位相のプロパーな伝達関数

\begin{align}
G(s) &= \frac{(s - z_1)(s - z_2) \cdots (s - z_m)}{(s - p_1)(s - p_2) \cdots (s - p_n)} \\
n &\geq m \\
 z_i &< 0  （ i = 1, \cdots, m ）, p_k < 0  （ k = 1, \cdots, n）
 
\end{align}

を考える。ただし、上式では高位の極・零点を位数の分だけ繰り返し数え上げてあるものとする。$m$個の零点
$z_1, \cdots, z_m$に1対1に対応するように$m$個の極$p_1, \cdots, p_m$を選んで、
$|z_i| > |p_i|$、すなわち、$z_i < p_i$
を満たすようにできれば、$G(s)$のステップ応答には行き過ぎが生じないことが導ける²

この性質ですが、いくつか注意が必要です。

• おそらく、伝達関数が実極・実ゼロ点のみを持ち、重極や重ゼロ点を持たない場合の条件である
• オーバーシュートではなく、「ステップ応答が極大値を持たない」ことに関する条件である
• あくまで「ステップ応答が極大値を持たない」ことへの十分条件であり、これを満たさなくても、ステップ応答が極大値を持たないことがある → 後述の例で確認します

オーバーシュートと「ステップ応答が極大値を持たない」のは微妙に違います。定常値に至るまでに信号として変曲点があっても、定常値を超えないことがあるからです(前回記事も参照)。

また、この性質に関してはちょっとわかりにくいので、元文献²までさかのぼって参照しつつ自分の言葉で述べると、下記の内容だと思われます。

ゼロ点$z_1, \cdots, z_m$、極$p_1, \cdots, p_n$を小さい順(つまり虚軸から離れている順)に並べてあるものとする。小さい順にとってきた$m$個のゼロ点と極のペアに対し、すべて$z_i < p_i (i = 1,\cdots,m)$ならステップ応答は極大値を持たない。

↑でいう$z_i<p_i$は、ペアになった極とゼロ点のうち、ゼロ点の方が常に左半平面の負側にある、ということを表しています。※これ以降は$z$や$p$の符号を変えるので、大小関係が逆になります。

これに対し本記事では、具体例を考えて解析していくにあたり、まずは上記の命題を下記のように改変します。

伝達関数

\begin{align}
G(s) &= \frac{(s + z_1)(s + z_2)}{(s + p_1)(s + p_2)} 
\end{align}

を考える。ただし、$z_2>z_1>0$、$p_2>p_1>0$とし、極とゼロ点はいずれも実数とする。このとき、$z_1>p_1$かつ$z_2>p_2$ならステップ応答が極大値を持たない。

もとの命題と異なり、下記の変更を加えています。

• 2次の実極・実ゼロ点のみで、重複なしと明記した
• 極とゼロ点の符号を変えた

極とゼロ点の符号を変えたことで、下図のような意味合いになっています。図中でpやzにマイナスの符号がついていることに注意ください。$p_1$、$p_2$、$z_1$、$z_2$そのものは正の値ですが、伝達関数の極としては逆の符号になります。したがって、下図は$z_2>p_2$、$z_1>p_1$の極ゼロ配置を表しています。大なり、の左辺の方が左半平面の負側寄り、という意味となっています。
(後々出てくる不等式を少しでもわかりやすくしたく、$p$や$z$を正の数にする意図があります)

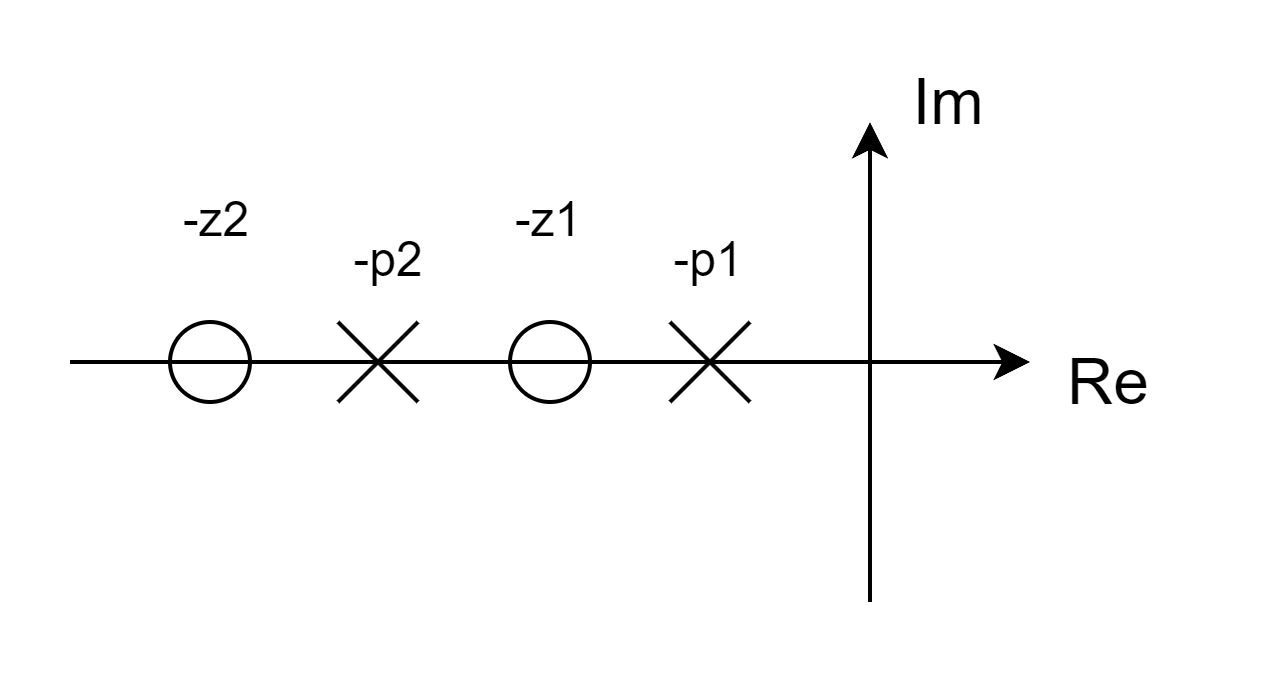
以下この条件に沿って例を挙げて、極ゼロの配置によってオーバーシュートがどう変わるか確認してみます。

色々極配置を試して確認していきますが、先にもう一つ注意を述べておきます。以下では、

\begin{align}
G(s) &= \frac{(s + z_1)(s + z_2)}{(s + p_1)(s + p_2)} 
 
\end{align}

の2次の伝達関数を考えます。ただし、ステップ応答のオーバーシュートを確認するにあたって、定常ゲインを調整しないと都合が悪いです。どういうことかというと、上記伝達関数のステップ応答の定常値は、最終値の定理により

\begin{align}
G(0) &= \frac{(0 + z_1)(0 + z_2)}{(0 + p_1)(0 + p_2)}  = \frac{z_1 z_2}{p_1 p_2}
\end{align}

となります。これだと定常値が極ゼロによってコロコロ変わって比較しづらいため、

\begin{align}
T(s) &= \frac{p_1 p_2}{z_1 z_2} \frac{(s + z_1)(s + z_2)}{(s + p_1)(s + p_2)} 
\end{align}

を考えることとします。この伝達関数のステップ応答の定常値は1になるものの、そのぶん初期値がずれます。ずれた初期値によって、冒頭のオーバーシュート定義に登場したような波形がしばしば現れます。

ステップ応答が極大値を持たない例

例を挙げると、下記の極配置の2次の伝達関数は、どちらも$z_1 > p_1$、$z_2 > p_2$を満たしています。大なり、の左辺の方がより左半平面の負側にある、という点に注意ください。

この伝達関数の応答を確認するMATLABコードは下記です(Control System Toolboxが必要です)。zpk関数の第3引数に「prod([極のリスト])/prod([ゼロ点のリスト])」を渡すことで、先述の定常ゲインの調整ができます。

T1 = zpk([-3 -4],[-1 -2],prod([-1 -2])/prod([-3 -4]));
T2 = zpk([-2 -4],[-1 -3],prod([-1 -3])/prod([-2 -4]));
step(T1, T2, 10)

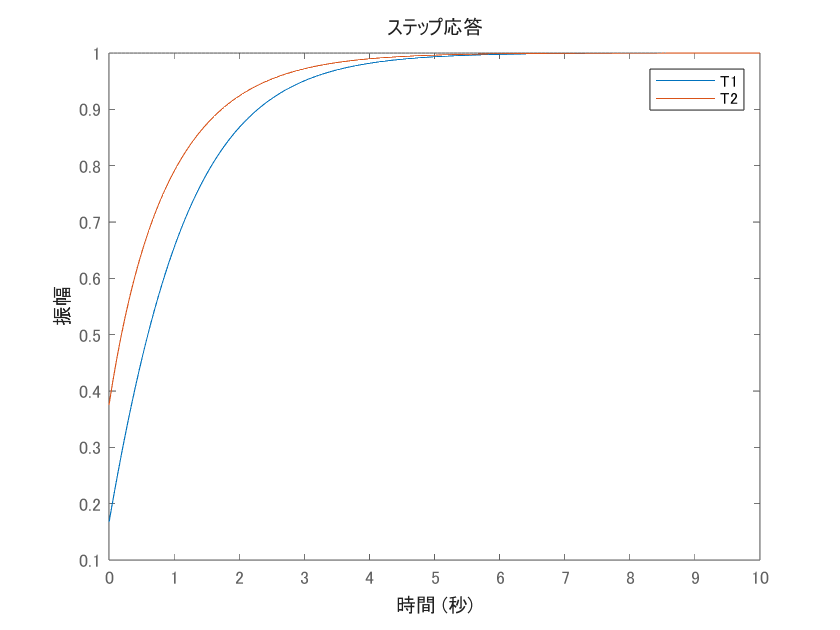
波形を確認すると、意図通りどちらも極大値が生じていません。極大値が生じてないため、オーバーシュートも生じていません。先ほどの条件を満たすと、オーバーシュートは起きないことがわかります。

ステップ応答が極大値を持たないはずの例

先の条件を満たさない例も試してみます。
下記はいずれも、$z_1 > p_1$か$z_2 > p_2$のどちらか(もしくは両方)を満たしていません。

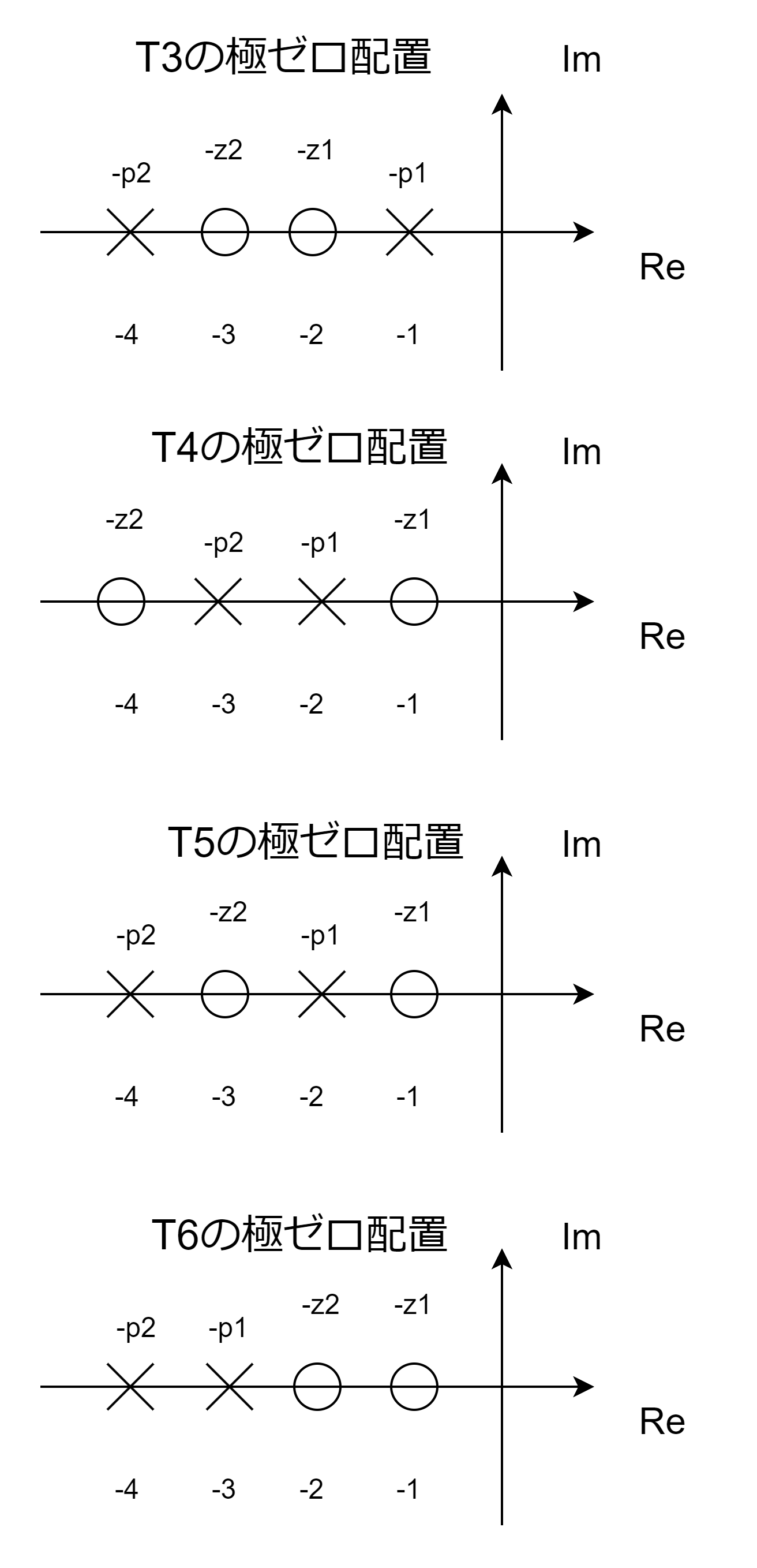
T3 = zpk([-2 -3],[-1 -4],prod([-1 -4])/prod([-2 -3])); %こちらは極値を持たない
T3_2 = zpk([-2 -3],[-1.5 -4],prod([-1.5 -4])/prod([-2 -3])); %↑と順序関係は同じだが、こちらは極値を持つ
T3_3 = zpk([-2 -3],[-1.7 -4],prod([-1.7 -4])/prod([-2 -3])); %↑と順序関係は同じだが、こちらは極値を持つうえ、オーバーシュートもする。
T4 = zpk([-1 -4],[-2 -3],prod([-2 -3])/prod([-1 -4]));
T5 = zpk([-1 -3],[-2 -4],prod([-2 -4])/prod([-1 -3]));
T6 = zpk([-1 -2],[-3 -4],prod([-3 -4])/prod([-1 -2]));
pzmap(T3, T3_2, T3_3, T4, T5, T6);
step(T3, T3_2, T3_3, T4, T5, T6, 6);
legend({'T3', 'T3_2', 'T3_3', 'T4', 'T5', 'T6'})
ylim([0 1.6]);

上記で注目すべきは、T3の応答です。先の条件によれば極大値を持つはずが、極大値も持たず、オーバーシュートもしていません。

さらに、T3の極ゼロの大小関係をそのままに、T3_2とT3_3という伝達関数もプロットしています。結果、下記のことがわかります。

• T3_2 は極大値を持つ(前回記事で述べた、極大値を持つけどオーバーシュートしない、という例)
• T3_3 は極大値を持つし、オーバーシュートもする

T3_2は前回記事のノッチフィルタのステップ応答と酷似しています。実極・実ゼロだけでノッチフィルタ状の特性を作れるのは興味深いですが、話が脱線するのであまり深堀しません。

T3、T3_2、T3_3の極ゼロ配置は下図のようになっています。

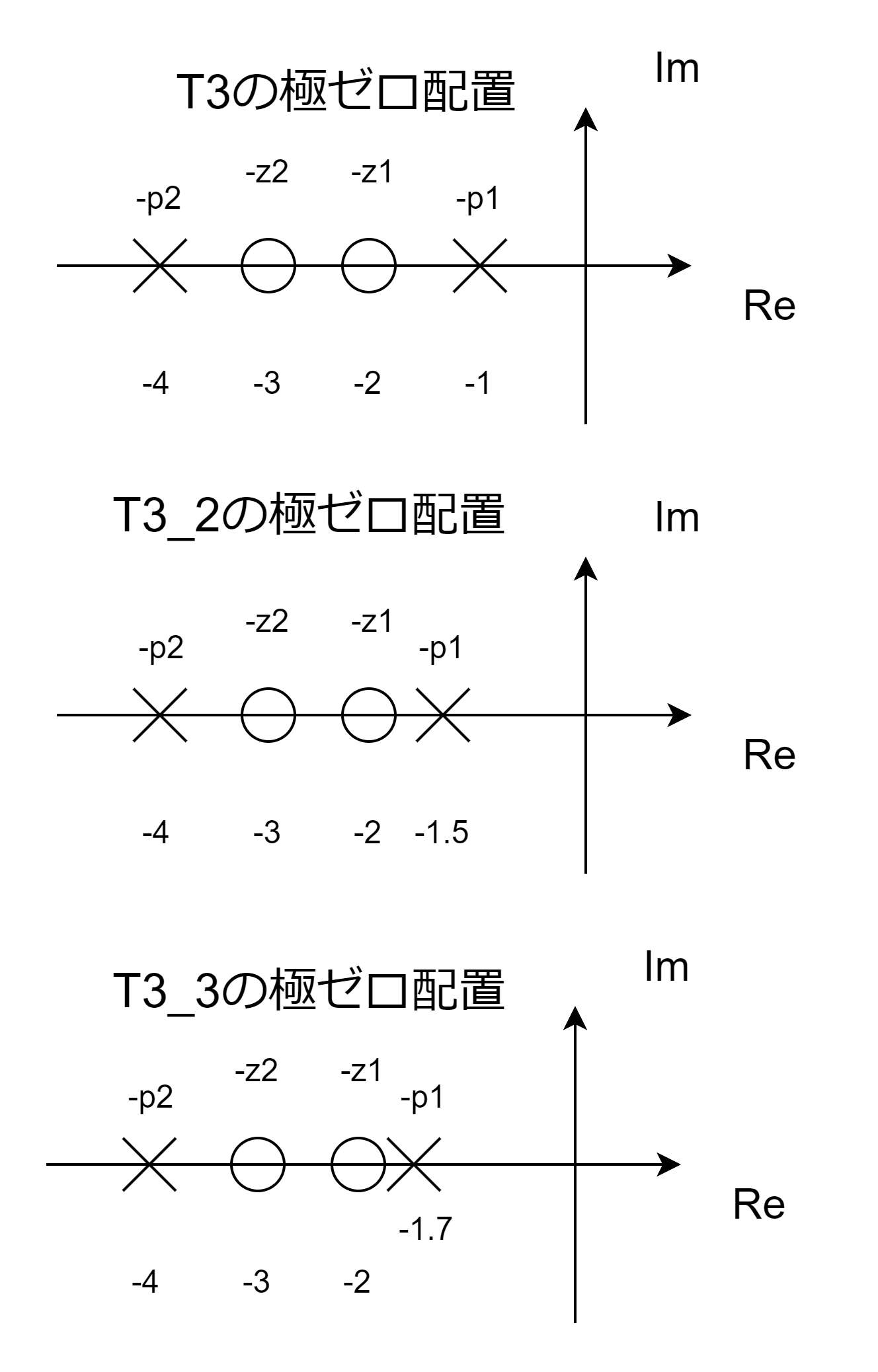
上記の例のとおり、ゼロ点を持つ伝達関数は、極やゼロ点が少しずれただけで、ステップ応答が極大値を持つようになってしまいます。もちろん、先の条件が嘘を言っているわけではなく、あくまで「この条件を満たすと極大値を持たない」という十分条件であり、「この条件を外れたものがすべて極大値を持つ」ということは言ってなかったわけです。しかも上記条件は極大値の有無に関してです。工学的には、一瞬でも定常値を超えるか否かの条件が気になります。

では、伝達関数のオーバーシュート有無をより精緻に見分けるにはどうしたらいいでしょうか？ …ということで、長かったですがここまでが前置きです。いよいよ本題に入っていきます。

2次の極ゼロを持つ伝達関数の解析

本記事では

• 2次の伝達関数
• 安定かつ実数の極ゼロのみを扱う

に限って、オーバーシュート有無の条件がどこで切り替わるかを確認します。方針としては、愚直に逆ラプラス変換をすることでステップ応答の解析をします。最初に入れた縛りによって今回は解析的に判定できますが、一般の場合には難しい、という様子が伝わればと思います。

伝達関数のゼロ点について

まず、おさらい的にゼロ点とは何なのか、を述べます。

単一ゼロ点の場合

文献³ (pdf版は無料で見れます)の4.8節によると、伝達関数の極は「その制御対象の応答のモード」を表す一方、ゼロ点は「それらモードの足される割合」を表します。その意味で、ゼロ点は極に比べて素性がわかりにくいです。

具体的に、ゼロ点を含む系の例をあげます。下記はゼロ点$c$を持つ伝達関数です。($s+c$というような表現ではなく$\frac{1}{c}s+1$という表現なのは、↑でも触れた定常ゲインの調整を不要にするためです。)

\begin{align}
H(s) &= \frac{-\frac{1}{c}s+1}{(s+1)(\frac{1}{2}s+1)} 
\end{align}

この伝達関数のステップ応答は、

\begin{align}
\frac{H(s)}{s} &= \frac{1}{s}\frac{-\frac{1}{c}s+1}{(s+1)(\frac{1}{2}s+1)} \\
&= \frac{1}{s} - \left(2+\frac{2}{c}\right)\frac{1}{s+1}+\left(1+\frac{2}{c} \right)\frac{1}{s+2} \\
\end{align}

上記を逆ラプラス変換することで下記のとおり求められます。

\begin{align}
y(t) &= 1 - \left(2+\frac{2}{c}\right)e^{-t}+\left(1+\frac{2}{c} \right)e^{-2t}\\
\end{align}

上記の式で、ゼロ点$c$がステップ応答に与える影響がざっくりわかります。まず、$c$が-1に近づいた場合、第2項の$e^{-t}$に関しての挙動がキャンセルされます。同様に$c$が-2に近づいた場合も、第3項の$e^{-2t}$に関しての挙動がキャンセルされます。このように、ゼロ点はある意味での「応答モードの足される重み・割合」のようなかたちで効いてきます。

また、$c$の絶対値が大きいとき、$c<0$の安定ゼロ・$c>0$の不安定ゼロどちらの場合も、ゼロ点の影響は小さくなります。これは極と似ていて、「応答が速い極の影響は無視できる」に類似の性質がゼロ点にも言えます。逆に$c$の絶対値が小さい(虚軸に近い)場合、ゼロ点の影響はより顕著に表れます。$c<0$の安定ゼロの場合にはオーバーシュートのかたちで、$c>0$の不安定ゼロの場合はアンダーシュートのかたちで特徴的な挙動となります。

ここで述べた内容は、↓の読書メモも参考にさせていただきました。

上記は複素成分を持つゼロ点についても言えます。複素成分のゼロ点を持つ伝達関数をボード線図などで描画すると、特定の周波数帯のノッチ特性としてあらわれてきます。こうした場合はより直感的に「ある周波数成分の振動を減衰させる・取り除く」という解釈ができます。

複数のゼロ点をもつ場合

ゼロ点が複数になると、途端にややこしくなってきます。極やゼロ点に重複が無い下記の伝達関数($n\geq m$)を考えた場合、

\begin{align}
G(s) = \frac{b_m(s+z_1)(s+z_2)\cdots(s+z_m)}{(s+p_1)(s+p_2)\cdots(s+p_n)}
\end{align}

このステップ応答は

\begin{align}
\frac{G(s)}{s} = \frac{1}{s} + \frac{h_1}{s+p_1} + \frac{h_2}{s+p_2} + \cdots + \frac{h_n}{s+p_n}
\end{align}

と表されます。ここで、各項の係数は

\begin{align}
h_i &= \lim_{s\rightarrow -p_i}\frac{(s+p_i) \ G(s)}{s}
\end{align}

で求めることができます。なぜそうなるの？は下記のヘビサイドの展開定理の解説が大変わかりやすいので参考にしてください。

具体的な$h_i$はけっこう複雑です。極限は代入で置き換えることができ、式で表すと下記となります。

\begin{align}
h_i &= \frac{b_m(z_1-p_i)(z_2-p_i)\cdots(z_m-p_i)}{(-p_i)(p_1-p_i)(p_2-p_i)\cdots(p_{i-1}-p_i)(p_{i+1}-p_i)\cdots(p_n-p_i)}
\end{align}

定性的には、「そのモードを表す極を中心に、全てのゼロ点・全ての極との距離を重みとして係数が決まる」というようなことが言えそうです。ある程度秩序だっているように見えますが、この係数がオーバーシュートの判定にとってはなかなか曲者となります。

$h_i$の例を示すとこんな感じです

例えば分母4次、分子3次の伝達関数の$h_2$は下記のようになります。分母分子の計算も図示してみました。何かがわかりそうで、そうでもないようで…というもどかしい図になっています。複素極に対してはもっとややこしいことになりそうですね。

2次の伝達関数の逆ラプラス変換

話を本題の2次の伝達関数に戻します。$T(s)$のステップ応答は、下式を逆ラプラス変換することで得られます。

\begin{align}
\frac{T(s)}{s} &= \frac{p_1 p_2}{z_1 z_2} \cdot \frac{1}{s}  \frac{(s + z_1)(s + z_2)}{(s + p_1)(s + p_2)} 
\end{align}

以降、定常ゲインの調整に出てくる係数は下記の通り$k$とおきます。

\begin{align}
k &= \frac{p_1 p_2}{z_1 z_2} 
\end{align}

部分分数分解すると、下記の形となります。

\begin{align}
\frac{T(s)}{s} &= k \left( \frac{A}{s} + \frac{B}{s+p_1} + \frac{C}{s+p_2}  \right)
\end{align}

具体的な$A$,$B$,$C$の式は、先述のヘビサイドの展開定理を利用して、下記のとおり求まります。$B$と$C$は後々のために、分母を正の値でそろえておきます。

\begin{align}
A &= \frac{z_1 z_2}{p_1 p_2}, \\
B &= \frac{(z_1-p_1)(z_2-p_1)}{p_1(p_1-p_2)} = -\frac{p_2(z_1-p_1)(z_2-p_1)}{p_1p_2(p_2-p_1)}, \\
C &= \frac{(z_1-p_2)(z_2-p_2)}{p_2(p_2-p_1)} = \frac{p_1(z_1-p_2)(z_2-p_2)}{p_1p_2(p_2-p_1)} 
\end{align}

上述の$T(s)/s$を逆ラプラス変換した結果、時間応答として下記の式が得られます。これがステップ応答です。

\begin{align}
y(t) &= k \left( A + B e^{-p_1 t} + C e^{-p_2 t} \right) \\
\end{align}

この時間応答について、下記のことが言えます。

• 第2項、第3項は時間とともにゼロに向かう関数なので、定常値は$kA=1$ (もちろん、意図して定常値が1となるように$k$をかけたので当然でもある)
• 初期値は$k(A+B+C)$で決まる

あとは$A$,$B$,$C$によって決まる大小関係で、定常値1に至る途中でオーバーシュートするかどうかが決まります。
この大小関係を整理していく作業となります。

オーバーシュートしないための条件①

まず、実は$A+B+C$は必ず1になります。
実際計算してみると、

\begin{align}
A+B+C &= \frac{z_1 z_2}{p_1 p_2} -\frac{p_2(z_1-p_1)(z_2-p_1)}{p_1p_2(p_2-p_1)}  + \frac{p_1(z_1-p_2)(z_2-p_2)}{p_1p_2(p_2-p_1)} \\
 &= \frac{z_1 z_2 (p_2 - p_1) -p_2(z_1-p_1)(z_2-p_1) + p_1(z_1-p_2)(z_2-p_2)}{p_1p_2(p_2-p_1)}  \\
 &= \frac{z_1 z_2 (p_2 - p_1) -p_2(z_1 z_2 - (z_1 + z_2)p_1 + p_1^2) + p_1(z_1 z_2 - (z_1 + z_2)p_2 + p_2^2)}{p_1p_2(p_2-p_1)}  \\
 &= \frac{ -p_2p_1^2 + p_1 p_2^2}{p_1p_2(p_2-p_1)}  = 1\\
\end{align}

したがって、先ほどのステップ応答$y(t)$の性質をあらためて書くと

• 第2項、第3項は時間とともにゼロに向かう関数なので、定常値は$kA=1$
• 初期値は$k(A+B+C)=k=1/A$で決まる

となっています。これらからわかるとおり、初期値$k=1/A$の大きさによって、定常値の1を超えるかどうかが決まります。本記事では一瞬でも定常値を上回ったらオーバーシュートという扱いなので、$k\leq1$,すなわち$A \geq 1$がオーバーシュートしないための一つの条件となります。下図のようなイメージです。

オーバーシュートしないための条件②

もう一つは、$B$と$C$の大小関係に着目すると導けます。定数倍や$A$によるオフセットは無視して$B e^{-p_1 t} + C e^{-p_2 t}$にだけ着目すると、下記の波形の足し合わせを考えることになります。この足し合わせが常に0以下であれば、$A$の足し合わせをしても定常値を超えることはありません。ひとつ重要な縛りとして、$p_2>p_1$とおいたため、かならず$C e^{-p_2 t}$の方が収束が早くなります。この点が不等式において重要となります。

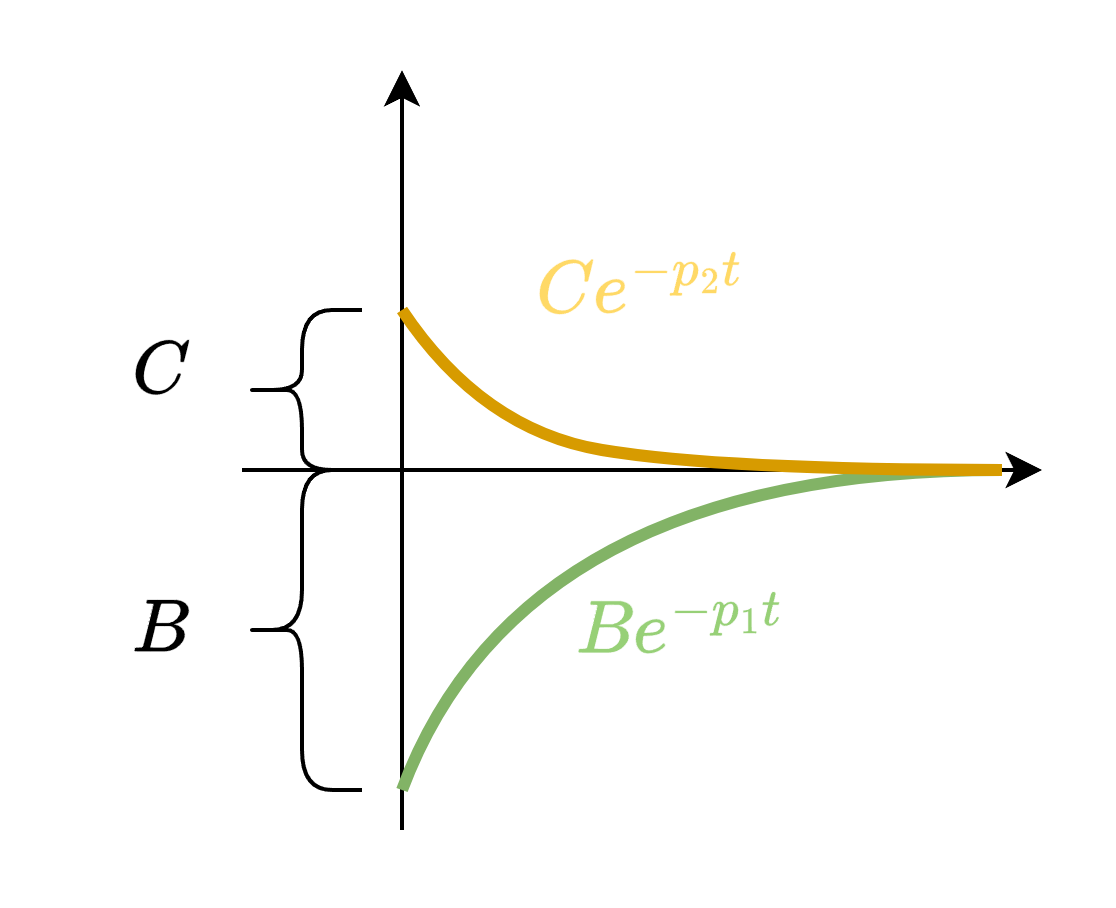
ここで、$B e^{-p_1 t} + C e^{-p_2 t}$の時間微分に着目して、その変化量の符号が変わらない条件を見て…としたくなりますが、これは(本記事にとっては)罠です。オーバーシュートしない条件のものには変化量の符号が変わるものがいるので、愚直に不等式を評価していくしかありません。

ので、ここからは場合分け大会となります。と言っても$B$と$C$の大小関係と符号についてだけなので、全部で8通りを見ればOKです。細かいことを言うと$|B|=|C|$となることはあり得ますが、話の大筋には影響ないので飛ばします。なお、$B=0$や$C=0$になることはありません。

ここで、明らかに足したら0を超えてしまうものには×を、明らかに0を超えることはないものには〇をつけると下記となります。⑦は一瞬迷いますが、赤く囲った部分で必ず0を超えてしまいます。

さらに、これまた判断迷う2列目の②と⑥も、足し合わせると赤の波形のようになってそれぞれ判別できます。ここで〇とした②は、緑点線(左隣の①と同一)のような大小関係になっていることを踏まえると常に〇と言えます。

この場合分けで、もう一つの条件が明らかになります。先に結論を述べると、オーバーシュートしないために必要なもう一つの条件は$B<0$です。

ここで、直前の図で×をつけたものを除外するために$|C|<|B|$や$C<0$の条件も必要そうですが、そうではありません。実は、$A \geq 1$と$B<0$によって、それら条件は自動的に満たされます。この点は若干ややこしいですが、後で確認することにします。

オーバーシュートしないための2つの条件

ここまでの状況を整理すると、

• オーバーシュートしないための1つ目の条件 $A \geq 1$
• オーバーシュートしないための2つ目の条件 $B < 0$

が得られています。この2条件が必要十分条件であるかまでは示せていませんが、限りなくそれに近いのではと思われます。

この2条件が極ゼロの位置として何を表しているかを整理します。
まず、$A \geq 1$ はそのまま $A = \frac{z_1 z_2}{p_1 p_2} \geq 1$を表します。
つづいて$B<0$は

\begin{align}
B &= -\frac{p_2(z_1-p_1)(z_2-p_1)}{p_1p_2(p_2-p_1)}
\end{align}

の分母が$p_2>p_1$より常に正なので、「$z_1>p_1$かつ$z_2>p_1$」、もしくは「$z_1<p_1$かつ$z_2<p_1$」を表しています。しかし、後者の「$z_1<p_1$かつ$z_2<p_1$」の条件は$A\geq 1$と組み合わせると除かれます。

この点をわかりやすくするため、適当な正の実数$\alpha$によって$p_2=p_1 + \alpha$ と置くことを考えてみます。大小関係が混乱しやすいので念のため図示すると、下記のようになっています。

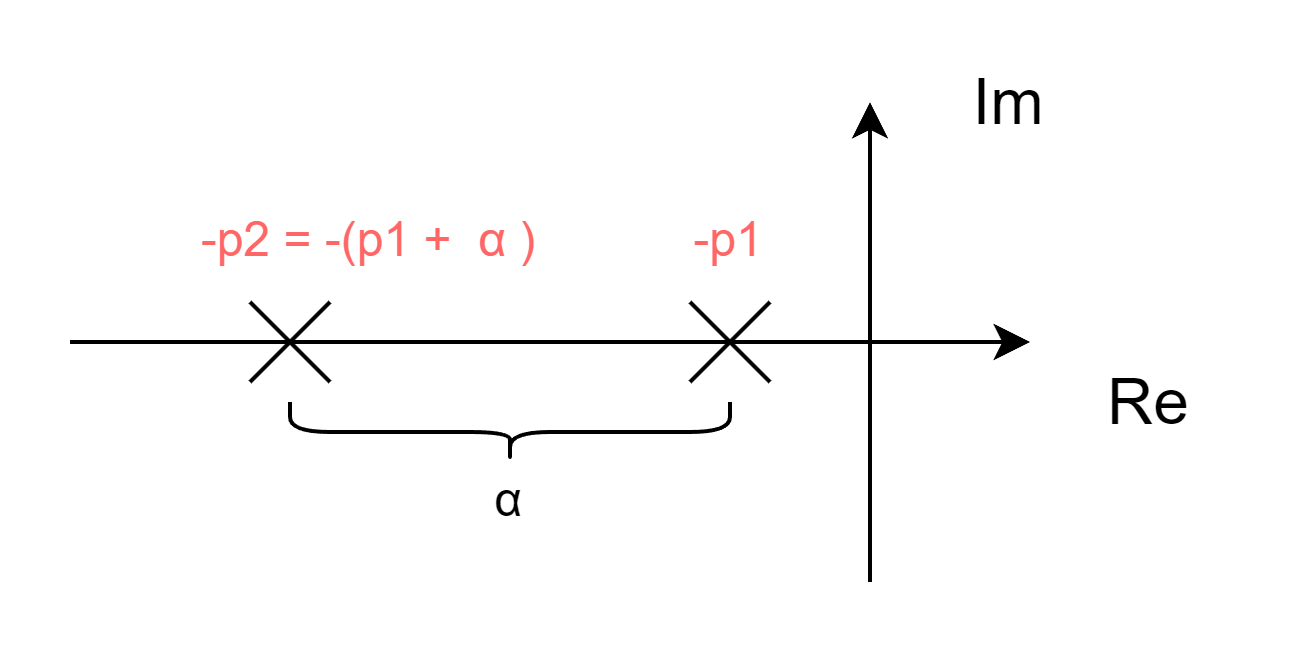
この置き換えで、$\frac{z_1 z_2}{p_1 p_2} \geq 1$ は $\frac{z_1 z_2}{p_1 (p_1 + \alpha)} \geq 1$となります。$\alpha$は正の実数なので、この不等式と「$z_1<p_1$かつ$z_2<p_1$」は明らかに矛盾しています。

これによって、

2次の実極・実ゼロを持つ伝達関数のステップ応答がオーバーシュートしないための条件は、極ゼロの位置に関して下記の２条件を満たすこと。

• 1つ目の条件 $z_1 z_2 \geq p_1 p_2 $
• 2つ目の条件 $z_1>p_1$かつ$z_2>p_1$

と言えます。2つ目にそこまで意外性はなく、「一番虚軸に近いのが実極となるべき」ということをあらわしています。一方、1つ目の条件はけっこう意外に思えるのではないでしょうか。この条件は極ゼロの配置の順序関係だけでなく、個々の値の大きさでも変わります。冒頭で極大値を持つはず…と思っていた(いわゆるT3の)波形のオーバーシュート有無はここで切り替わっていたわけです。
…と書いてた当初はこの1つ目の条件が非常に重要に思えたのですが、これはもしかしたらバイプロパな伝達関数限定かもですね…。厳密にプロパな伝達関数にそうした性質があらわれるかは微妙なところです。

|C| < |B| や C<0が不要であることの確認

先ほど示した⑥の条件が、$A\geq 1$のもとでは起きないことを確認します。
つまり、$A\geq 1$のもとでは⑥になることはなく、②や⑧に変わります。

条件⑥→⑧の確認

条件⑥と条件⑧の違いは、$C$の符号です。つまり、「$A\geq 1$かつ$B<0$かつ$|C|>|B|$のとき、必ず$C<0$になること」を確認していきます。

まず、$B$, $C$を再掲します。共通分母は正の実数となり、$p_*$とおくこととします。

\begin{align}
B &= -\frac{p_2(z_1-p_1)(z_2-p_1)}{p_1p_2(p_2-p_1)} = -\frac{p_2(z_1-p_1)(z_2-p_1)}{p_*}, \\
C &=  \frac{p_1(z_1-p_2)(z_2-p_2)}{p_1p_2(p_2-p_1)} = \frac{p_1(z_1-p_2)(z_2-p_2)}{p_*}
\end{align}

まず$B$について、両辺に係数をかけて式をわかりやすくします。$\frac{p_*}{p_1 p_2}$は正の数となる点に注意ください。

\begin{align}
\frac{p_*}{p_1 p_2}B &= -\frac{p_2}{p_1 p_2}(z_1-p_1)(z_2-p_1) \\
&= -\frac{p_2}{p_1 p_2}(z_1 z_2 -(z_1+z_2)p_1+p_1^2) \\
&= -\frac{z_1 z_2}{p_1 p_2}p_2 +(z_1+z_2)-p_1 \\
\end{align}

$A=\frac{z_1 z_2}{p_1 p_2}$と、先述の$p_2 = p_1 + \alpha$ (ただし$\alpha > 0 $)を再び使うと下式となります。

\begin{align}
\frac{p_*}{p_1 p_2}B &= -Ap_2 +(z_1+z_2)-p_1 \\
&= -p_1(A+1)-\alpha A +(z_1+z_2)\\
\end{align}

これによって、$B$を比較的わかりやすく書き表すことができました。
同様に、$C$も下記のとおり整理して書くことができます。$B$との違いは符号と第2項目です。

\begin{align}
\frac{p_*}{p_1 p_2}C &= p_1(A+1)+\alpha -(z_1+z_2)\\
\end{align}

ここで少し唐突ですが、得られた$B$、$C$の足し合わせを考えます。
再三ですが、$p_1$、$p_2$、$p_*$、$\alpha$、は全て正の値であることに注意ください。

\begin{align}
\frac{p_*}{p_1 p_2}(B+C)  &= \alpha - \alpha A \\
&= \alpha (1-A) \\
\end{align}

まずこの式に$A\geq 1$の条件を当てはめると、右辺は必ず非正(負かゼロ)の値になります。
さらに$B<0$、$|C|>|B|$の条件を当てはめると、上式の右辺が非正で成立するために必ず$C<0$でなければならないことが導けます。これで条件⑥→⑧が示せました。

条件⑥→②の確認

条件⑥と条件②の違いは、$B$と$C$の大小関係です。つまり、「$A\geq 1$かつ$B<0$かつ$C>0$のとき、必ず$|C|<|B|$になること」を確認していきます。

これも、先に求めた

\begin{align}
\frac{p_*}{p_1 p_2}(B+C)  &= \alpha (1-A) \\
\end{align}

の式から示せます。
まずこの式に$A\geq 1$の条件を当てはめると、右辺は必ず非正(負かゼロ)の値になります。
さらに$B<0$、$C>0$の条件を当てはめると、上式の右辺が非正で成立するためには必ず$|C|<|B|$の大小関係でなければならないことが導けます。これで条件⑥→②が示せました。

以上で、$A\geq 1$のもとでは条件⑥は起きず、条件②か⑧になることが示せました。

各条件でのステップ応答のプロット

各条件についての理解が深まったので、先の8つの条件に従う適当な極ゼロ配置を試行錯誤で見繕い、シミュレーションで応答を確認してみます。下記のMATLABコードを実行します。

PoleZero_Pattern8.m

pz_list = {[2 5 1 4],... % パターン①
    [1 2 3 4],... % パターン②
    [2 3 1 5],... % パターン③
    [1 3 2 4],... % パターン④
    [2 4 1 3],... % パターン⑤
    [1 8 2 3],... % パターン⑥
    [2 3 1 7],... % パターン⑦
    [5 10 6 16],... % パターン⑧
    };

figure;
colororder(["#0072BD";"#77AC30";"#EDB120"])
tiledlayout(2,4, 'TileSpacing', 'compact', 'Padding', 'compact');
for i=1:8
    nexttile;
    p_1 = pz_list{i}(1);
    p_2 = pz_list{i}(2);
    z_1 = pz_list{i}(3);
    z_2 = pz_list{i}(4);

    A{i}=(z_1*z_2)/(p_1*p_2);
    B{i}=-(z_1-p_1)*(z_2-p_1) / (p_1*(p_2-p_1));
    C{i}=(z_1-p_2)*(z_2-p_2) / (p_2*(p_2-p_1));
    T{i}=zpk(-[z_1 z_2],-[p_1 p_2], prod(-[p_1 p_2])/prod(-[z_1 z_2]));

    [y,t] = step(T{i},6);

    SecondTerm = B{i}/A{i}*exp( -p_1*t);
    ThirdTerm = C{i}/A{i}*exp( -p_2*t );
    
    plot(t, y, t, 1+SecondTerm, t, 1+ThirdTerm, 'LineWidth', 1.5);
    text(2.5,1.8,sprintf('A=%.2f',A{i}));
    text(2.5,1.6,sprintf('B=%.2f',B{i}));
    text(2.5,1.4,sprintf('C=%.2f',C{i}));
    
    text(1.5,0.5,sprintf('p1,p2,z1,z2\n =%d,%d,%d,%d',p_1,p_2,z_1,z_2));
    grid on;
    title(sprintf('Pattern %d', i));
    ylim([0 2]);  
end

場合分けの説明で使った図と、実行結果を載せると下記です。青線が、実際の伝達関数のステップ応答を表します。各グラフの上部には$A$、$B$、$C$の係数を載せ、下部には極ゼロの値(にマイナスをかけたもの)を載せています。

結果としては、今までの議論通りのプロットになっている様子です。条件⑦が一番「オーバーシュート」感のある波形となっています。②、④、⑧は意図通りオーバーシュートしていないこともわかります。「初期値で定常値を超えてるものをオーバーシュートと呼ぶのは邪道だ！」という方は、$A\geq 1$の条件(②，④、⑦、⑧)を眺めると良いと思います。

同様のコードで、極大値を持たないはず、の例で紹介したT3、T3_2、T3_3もプロットしてみます。結果は下記となります。

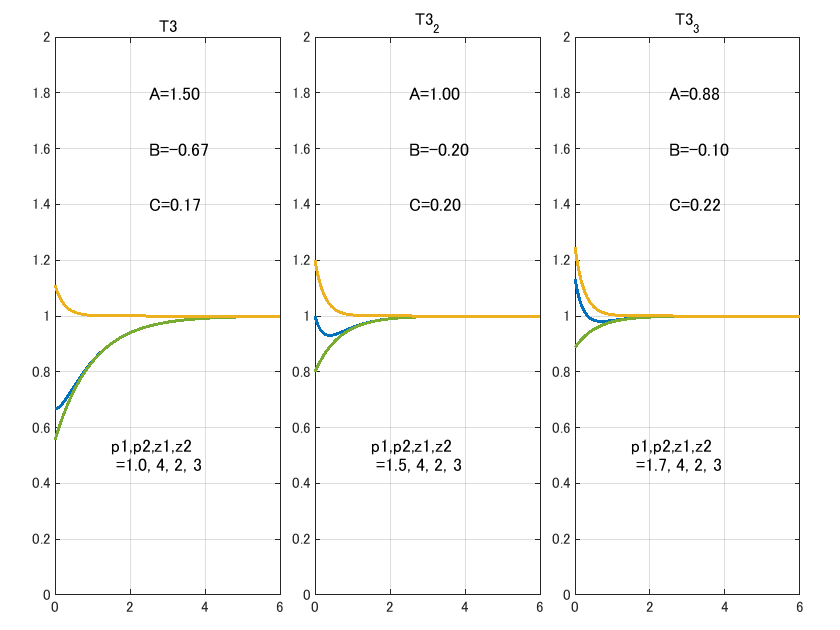
結果的に、条件②→(条件②と⑥の境界)→条件⑥ というかたちで推移してオーバーシュート有無が決まっていった様子がわかります。

この応答を見ると、ステップ応答の挙動が読みにくい原因が直感的にわかります。虚軸に最も近いp1をずらしたことで係数$B$に関連する指数減衰の応答(緑)が時間的にスライドしていますが、合わせて$C$の大きさも変わっています。この連動する係数の大小関係が見積もりづらいため、極やゼロを少し変えただけで波形が大きく異なったもののように見えていた、と言えそうです。

より一般的なオーバーシュート判定条件

最後に申し訳程度ですが、より一般的な条件に関わる文献をもう一つ紹介します。

文献⁴では、より一般的なオーバーシュートとゼロ点の関係が示されています。この文献では、オーバーシュートの種類を「定常値を何回超すか」で下図のように3つに場合分けしています。

考え方としてはとても興味深いです。↓の図のように

• オーバーシュートしない波形(青)は「必ず負側から定常値に近づくため、時刻∞で定常値を微妙に下回り続ける」
• 奇数型オーバーシュートの波形(赤)は「必ず正側から定常値に近づくため、時刻∞で定常値を微妙に上回り続ける」

という性質に着目しています。奇数型であれば判定条件を明確化できるようです(偶数型はそれでも切り分けできませんが…)。
以下に一部を引用します。

つぎのような伝達関数で示される単入力単出力システムを考える.

\begin{align}
G(s) &= \frac{b_{n-1}s^{n-1}+ \cdots + b_1 s + b_0}{s^{n}+ a_n s^{-1} \cdots + a_0} \tag*{(1)}
\end{align}

(中略)
<<定理1>>
システム(1)のステップ応答に無限型オーバーシュートがあらわれる必要十分条件は支配的な固有値が複素数となることである.

(中略)
<<定理2>>
システム(1)のステップ応答に奇数型オーバーシュートが表われる必要十分条件は, 支配的な実固有値より大きい負の実零点が奇数個存在することである。(定理1より支配的な固有値は実数でなければならない)

個人的に気になる点として、「支配的な」という表現に含みがあるように思えます。これを「最も虚軸に近い」と置き換えていいのかが判断つきませんでした。とはいえせっかっくなので、<<定理2>>についてその一部を紹介します。文献内では極やゼロ点の重複がある場合も含めた一般的な内容が述べられていますが、そうした重極・重ゼロ点となるケースを除外すると比較的シンプルにあらわせます。

※※以下では、文献内の記述に合わせるため再び極ゼロの符号を元に戻します。

極やゼロ点の重複が無いものとして、下記の伝達関数を例として文献の内容を後追いしてみます。

\begin{align}
H(s) &= \frac{(s - z_1)(s - z_2)}{(s - p_1)(s - p_2)(s - p_3)}
\end{align}

この伝達関数のステップ応答を$y(t)$とすると、$\dot{y}(t)$はインパルス応答であり、逆ラプラス変換によって下記のようにあらわされます。

\begin{align}
\dot{y}(t) &= \mathcal{L}^{-1} \left[ H(s)\right] \\
&= \left[ \frac{(s-z_1)(s-z_2)}{(s-p_2)(s-p_3)}\right]_{s=p_1} e^{p_1 t} + \left[ \frac{(s-z_1)(s-z_2)}{(s-p_1)(s-p_3)}\right]_{s=p_2} e^{p_2 t} + \left[ \frac{(s-z_1)(s-z_2)}{(s-p_1)(s-p_2)}\right]_{s=p_3} e^{p_3 t} \\
&=  \frac{(p_1-z_1)(p_1-z_2)}{(p_1-p_2)(p_1-p_3)} e^{p_1 t} + \frac{(p_2-z_1)(p_2-z_2)}{(p_2-p_1)(p_2-p_3)} e^{p_2 t} + \frac{(p_3-z_1)(p_3-z_2)}{(p_3-p_1)(p_3-p_2)} e^{p_3 t}
\end{align}

上式の指数関数にかかっているのは「複数のゼロ点をもつ場合」のところで紹介した係数$h_i$(の、極ゼロの符号が変わったもの)です。

ここで、系で最も支配的な(つまり、虚軸に近い)極を$p_1$とし、下記の$\xi(t)$という関数を定義します。

\begin{align}
\xi(t) &= \frac{(p_1-p_2)(p_1-p_3)}{e^{p_1 t}}
\end{align}

この$\xi(t)$は必ず正の値となることに注意ください。符号が大変ややこしいですが、$p_2<p_1<0$、$p_3<p_1<0$となるため分子は正×正となっています。

$\xi(t)$をステップ応答の時間微分(つまりインパルス応答)にかけると下式となります。

\begin{align}
\dot{y}(t) \xi(t) &=  (p_1-z_1)(p_1-z_2) - \frac{p_1-p_3}{p_2-p_3}(p_2-z_1)(p_2-z_2) e^{(p_2-p_1) t} \\ 
& \quad - \frac{p_1-p_2}{p_3-p_2}(p_3-z_1)(p_3-z_2) e^{(p_3-p_1) t}
\end{align}

上式は$p_2<p_1$、$p_3<p_1$なので、時刻が十分経つと第2・第3項目はゼロであり、下記となります(ここもちょっと引っ掛かります。$p_2$や$p_3$に複素成分があった場合にも以降の議論は成り立つんでしょうか…)。

\begin{align}
 \lim_{t \rightarrow \infty} \dot{y}(t) \xi(t) &= (p_1-z_1)(p_1-z_2) 
\end{align}

奇数型オーバーシュートの特徴である「必ず正側から定常値に近づくため、時刻∞で定常値を微妙に上回り続ける」は、すなわちステップ応答の時間変化が時刻∞で負になることであり、下記の性質を指しています。

\begin{align}
 \lim_{t \rightarrow \infty} \dot{y}(t) &= -0
\end{align}

$\xi(t)$は常に正の値となって符号を変えることはないため、

\begin{align}
 \lim_{t \rightarrow \infty} \dot{y}(t) \xi(t) &=(p_1-z_1)(p_1-z_2) < 0
\end{align}

を満たす、つまり支配的な$p_1$より正側に大きい実零点の個数が奇数だと、奇数型オーバーシュートが起こる…というわけです。

なお、$z_1$と$z_2$がどちらも$p_1$より大きい、というケースでは上式を満たしません。そのケースでオーバーシュートが起きないわけではなく、あくまで上記は「奇数型オーバーシュート」の判定条件であることに注意してください。

こうした使いづらい点はあり、やはりオーバーシュートの判別条件に一定の制約はつきもののようです。それでもなお興味深い内容なので、オーバーシュートが気になる方は元文献を参照ください。

おわりに

2次の実極・実ゼロを持つ伝達関数について、ステップ応答がオーバーシュートする(極力必要十分に近そうな)条件について紹介しました。

つくづくゼロ点の影響は見積もりづらいです。バイプロパな伝達関数限定かもですが、極ゼロの大きさの順序関係だけでなく、値そのもので振る舞いが変わるのはけっこう意外でした。もちろん、3次以上の伝達関数は場合分けで確認するのがかなり難しくなります。より高次の伝達関数でオーバーシュートするかしないかは「だいたいこう」ということは言えても、厳密に示すのは難しい、というのが実感としてわかりました。

以下、もう少し補足…

今回、記事の量のわりに、裏での調査や検証の労力はなかなかのものでした。動いたらヨシ！の工学系数学よわよわ民にとって、不等式の評価はかなりしんどいです。

もともと複素極・複素ゼロ点も含めた伝達関数を実軸上の順序関係で場合分けし、シミュレーションベースで検証するつもりでした。が、順序関係だけでなく個々の大きさでオーバーシュート有無は変わるかも…という点に途中で気づいて大きく方針転換しました。これらの内容もボツネタとしていずれ載せられたらと思います。

1. "システム制御シリーズ 古典制御理論―基礎編", 荒木 光彦, 培風館 ↩

2. "Some conditions on zeros to avoid step-response extrema,", A. Rachid, in IEEE Transactions on Automatic Control, vol. 40, no. 8, pp. 1501-1503, Aug. 1995, https://ieeexplore.ieee.org/document/402253/ ↩ ↩²

3. "Control System Design", Graham C. Goodwin, Stefan F. Graebe, Mario E. Salgado, Pearson College Div, http://caaelotel.elo.utfsm.cl/home/wp-content/uploads/Control-System-Design-SalgadoGoodwinGraebe.pdf ↩

4. "オーバーシュートと零点の関係", 小林 尚登, 計測自動制御学会論文集, 1985 ↩