はじめに
制御工学に関する記事を書こうと制御対象のモデルを作っていたところ、別記事にした方が良さそうな内容になったのでこちらにまとめます。
本記事では、MATLABのSymbolic Math Toolboxを使って2関節マニピュレータの運動方程式を求め、それをそのままSimulinkモデル化する手順について載せます。
まず下記の記事を参考に、運動方程式を求めてみます。
さらにSymbolic Math Toolboxの機能で、得られた方程式をMATLAB Functionブロックとしてエクスポートします。得られたブロックを整理・配線することで、下図のように2トルクを入力し、2角度が出力されるようなモデルを作っていきます。
なお、エクスポートされたこのMATLAB Functionブロックでのモデル自体は、Symbolic Math Toolboxが無くても動かせます。

最終的にこのモデルと、手動で運動方程式を求めて愚直に配置配線したSimulinkモデルと挙動が一致することを確認していきます。
2関節マニピュレータ
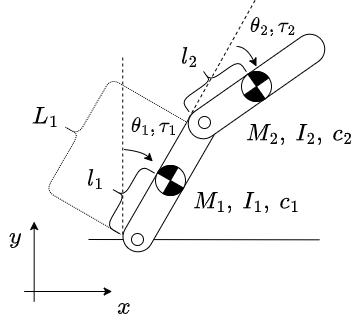
下図の2関節マニピュレータの運動方程式を導出し、Simulinkモデル化していきます。マニピュレータというより、2重剛体振り子そのものです。
ほぼ図を見てのとおりですが、重心と回転軸の間の距離を$l$、関節の長さを$L$と分けています。また、重心周りの慣性モーメントを$I$、各関節の減衰係数を$c$としています。
まったく同じ構成の運動方程式を導出している講義資料を見つけたので、パク 参考にしています。
運動方程式の導出過程はそちらを参照ください。
Symbolic Math Toolboxによる運動方程式
運動エネルギーと位置エネルギーを記述してLagrange関数を求め、それらの時間微分、一般化座標による偏微分を行っていくことで運動方程式を求めます。
clear;
syms M_1 M_2 L_1 l_1 l_2 g I_1 I_2 c_1 c_2 real % 物理パラメータ 実数値しかとらないので念のためreal
syms theta(t) [2 1] % [theta1(t)、theta2(t)]^T の定義
syms tau(t) [2 1] % [tau1(t)、tau2(t)]^T の定義
%--- 一般化座標qに関連する定義 ---
% q = theta ←こうしてしまうと、q(1)としたとき、q(t)|t=1の意味になってしまう。
% 台車型倒立振子などで並進運動を組み合わせるなら、q = [theta(t); x(t)];とかすれば良いはず
q = theta(t);
dq = diff(q,t);
ddq = diff(dq,t);
tau = tau(t); % qと同様、tの関数であることを省略表記するための置き換え
%--- 直交座標の定義と、それらの導関数の記述 ---
x_1 = l_1 * sin(q(1));
y_1 = l_1 * cos(q(1));
x_2 = L_1 * sin(q(1)) + l_2 * sin(q(1)+q(2));
y_2 = L_1 * cos(q(1)) + l_2 * cos(q(1)+q(2));
dx_1 = diff(x_1, q(1))*dq(1) + diff(x_1, q(2))*dq(2);
dx_2 = diff(x_2, q(1))*dq(1) + diff(x_2, q(2))*dq(2);
dy_1 = diff(y_1, q(1))*dq(1) + diff(y_1, q(2))*dq(2);
dy_2 = diff(y_2, q(1))*dq(1) + diff(y_2, q(2))*dq(2);
%--- Lagrange関数の記述 ---
K1 = 1/2*M_1*dx_1^2 + 1/2*M_1*dy_1^2;
K2 = 1/2*M_2*dx_2^2 + 1/2*M_2*dy_2^2;
Krot = 1/2*I_1*dq(1)^2 + 1/2*I_2*(dq(1)+dq(2))^2;
U1 = M_1*g*l_1*cos(q(1));
U2 = M_2*g*L_1*cos(q(1))+M_2*g*l_2*cos(q(1)+q(2));
L = (K1+K2+Krot) - (U1+U2);
D = [c_1*dq(1), c_2*dq(2)]; % 散逸項はあらかじめ微分してある
%--- Lagrange方程式による運動方程式導出---
N = length(q);
for i = 1:N
dLq(i) = diff(L, dq(i));
temp = 0;
for j = 1:N
temp = temp + diff(dLq(i),dq(j))*ddq(j) + diff(dLq(i),q(j))*dq(j);
end
ddLq(i) = temp;
eq(i) = ddLq(i) - diff(L,q(i)) == -D(i) + tau(i);
end
eq(1) % 得られた運動方程式の表示
eq(2) % 得られた運動方程式の表示
運動方程式の動作シミュレーション
得られた運動方程式は、そのまま簡単に動作シミュレーションが行えます。適当にパラメータ値と角度の初期値を与えて、動きを見てみます。
先のコードの続きです。
%% 初期値を与えた時の自由振動シミュレーション
L_1 = 2;
l_1 = 1;
l_2 = 1.5;
M_1 = 2;
M_2 = 1;
g = 9.8;
c_1 = 2;
c_2 = 2;
tau1 = 0; % 印可トルクなしの自由振動
tau2 = 0; % 印可トルクなしの自由振動
I_1 = 1/M_1*l_1^2; % 一様な剛体棒の慣性モーメント
I_2 = 1/M_2*l_2^2; % 一様な剛体棒の慣性モーメント
eqn_1 = subs(eq(1)); % シンボリック式のパラメータ値を置き換え
eqn_2 = subs(eq(2)); % シンボリック式のパラメータ値を置き換え
[V,S] = odeToVectorField(eqn_1,eqn_2);
% S = [theta2 dtheta2 theta1 dtheta1]の順
solveHandler = matlabFunction(V,'vars',{'t','Y'});
initCond = [pi/4 0 pi/6 0];
TimeLentgh = [0 20];
sols = ode45(solveHandler,TimeLentgh,initCond);
%% 描画
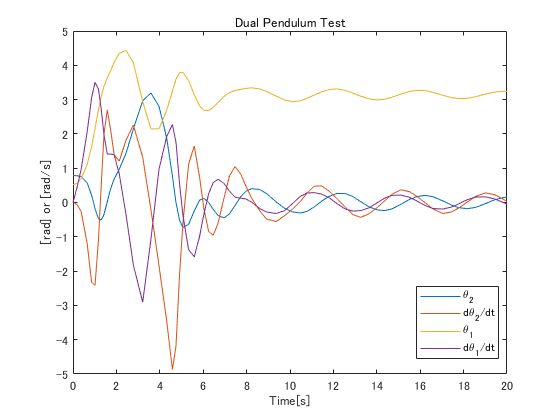
plot(sols.x,sols.y)
legend('\theta_2' , 'd\theta_2/dt', '\theta_1', 'd\theta_1/dt')
title('Dual Pendulum Test')
xlabel('Time[s]')
ylabel('[rad] or [rad/s]')
描画結果は下記です。この時点ではまだ確信持てないですが、初期値を与えて$\theta_1 = \pi$、$\theta_2 = 0$に落ち着いていってるので、まずまずあってそうな感じです。
Symbolic Math Toolboxで求めた運動方程式のSimulinkモデル化
得られた運動方程式をSimulinkモデル化していきます。上述のMATLABコードはあらかじめ角度等々を時間$t$の関数とし、ode45を使って微分方程式として解いていきました。しかし、MATLAB Functionブロックとしてエクスポートするにあたっては、代数方程式として記述していかなければならないようです。 dsolve関数を使えば解析解を求められそうですが、今回は代数方程式として解く方針でいきます。
そのため、先ほどと重複する部分も多いですが、下記のコードでモデルをSimulink化していきます。
コード内では、最初の$q$、$\dot{q}$、$\ddot{q}$の定義が、時間の関数ではなくただの別々の異なった3つ(添え字1と2があるので合計6つ)の記号になってることが重要です。
なんでこれで運動方程式が求まるかというと
\begin{align}
\frac{d}{dt}\left(\frac{\partial L(q_1,q_2,\dot{q}_1,\dot{q}_2)}{\partial \dot{q}_1} \right), \ \frac{d}{dt}\left(\frac{\partial L(q_1,q_2,\dot{q}_1,\dot{q}_2)}{\partial \dot{q}_2} \right)
\end{align}
の計算を、それぞれ全微分を用いて
\begin{align}
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_1} \right) &= \frac{\partial}{\partial q_1}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \frac{d q_1}{dt} + \frac{\partial}{\partial \dot{q}_1}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \frac{d \dot{q}_1}{dt} + \frac{\partial}{\partial q_2}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \frac{d q_2}{dt} + \frac{\partial}{\partial \dot{q}_2}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \frac{d \dot{q}_2}{dt} \\
&= \frac{\partial}{\partial q_1}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \dot{q}_1 + \frac{\partial}{\partial \dot{q}_1}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \ddot{q}_1 + \frac{\partial}{\partial q_2}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \dot{q}_2 + \frac{\partial}{\partial \dot{q}_2}\left(\frac{\partial L}{\partial \dot{q}_1} \right) \ddot{q}_2 \\
\\
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_2} \right) &= \frac{\partial}{\partial q_1}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \frac{d q_1}{dt} + \frac{\partial}{\partial \dot{q}_1}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \frac{d \dot{q}_1}{dt} + \frac{\partial}{\partial q_2}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \frac{d q_2}{dt} + \frac{\partial}{\partial \dot{q}_2}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \frac{d \dot{q}_2}{dt} \\
&= \frac{\partial}{\partial q_1}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \dot{q}_1 + \frac{\partial}{\partial \dot{q}_1}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \ddot{q}_1 + \frac{\partial}{\partial q_2}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \dot{q}_2 + \frac{\partial}{\partial \dot{q}_2}\left(\frac{\partial L}{\partial \dot{q}_2} \right) \ddot{q}_2
\end{align}
と時間$t$を含まない形に変形してくれているからです。元記事に感謝です。
最初の$q$、$\dot{q}$、$\ddot{q}$の定義以降、運動方程式を得るところまで は、まったく同じコードです。上手く書くと、先ほどのシミュレーション時のコードと共通化できるような気もしますがそこは手抜きしています。
clear;
syms M_1 M_2 L_1 l_1 l_2 g I_1 I_2 c_1 c_2 real % 物理パラメータ 実数値しかとらないので念のためreal
syms theta [2 1]
syms dtheta [2 1]
syms ddtheta [2 1]
syms tau [2 1]
%--- 一般化座標qに関連する定義 ---
q = theta;
dq = dtheta;
ddq = ddtheta;
%--- 直交座標の定義と、それらの導関数の記述 ---
x_1 = l_1 * sin(q(1));
y_1 = l_1 * cos(q(1));
x_2 = L_1 * sin(q(1)) + l_2 * sin(q(1)+q(2));
y_2 = L_1 * cos(q(1)) + l_2 * cos(q(1)+q(2));
dx_1 = diff(x_1, q(1))*dq(1) + diff(x_1, q(2))*dq(2);
dx_2 = diff(x_2, q(1))*dq(1) + diff(x_2, q(2))*dq(2);
dy_1 = diff(y_1, q(1))*dq(1) + diff(y_1, q(2))*dq(2);
dy_2 = diff(y_2, q(1))*dq(1) + diff(y_2, q(2))*dq(2);
%--- Lagrange関数の記述 ---
K1 = 1/2*M_1*dx_1^2 + 1/2*M_1*dy_1^2;
K2 = 1/2*M_2*dx_2^2 + 1/2*M_2*dy_2^2;
Krot = 1/2*I_1*dq(1)^2 + 1/2*I_2*(dq(1)+dq(2))^2;
U1 = M_1*g*l_1*cos(q(1));
U2 = M_2*g*L_1*cos(q(1))+M_2*g*l_2*cos(q(1)+q(2));
L = (K1+K2+Krot) - (U1+U2);
D = [c_1*dq(1), c_2*dq(2)]; % 散逸項はあらかじめ微分してある
%--- Lagrange方程式による運動方程式導出---
N = length(q);
for i = 1:N
dLq(i) = diff(L, dq(i));
temp = 0;
for j = 1:N
temp = temp + diff(dLq(i),dq(j))*ddq(j) + diff(dLq(i),q(j))*dq(j);
end
ddLq(i) = temp;
eq(i) = ddLq(i) - diff(L,q(i)) == -D(i) + tau(i);
end
eq(1) % 得られた運動方程式の表示
eq(2) % 得られた運動方程式の表示
%% MATLAB Function ブロックとしてエクスポート
try % モデルが存在しなければ新規作成。すでにあればそれを開く
new_system('test_system')
catch ME
open_system('test_system')
end
eqns = [eq(1),eq(2)];
S = solve(eqns,ddtheta1,ddtheta2); % 代数方程式として、thetaの2階微分について解く
matlabFunctionBlock('test_system/DualPendulum1', S.ddtheta1,... % theta1の2階微分を出力する演算ブロック作成
'vars',[I_1 I_2 L_1 M_1 M_2 c_1 c_2 g l_1 l_2 tau1 tau2 theta1 theta2 dtheta1 dtheta2],'outputs',{'ddtheta1'}) % 入力端子順序と出力端子名前を指示
matlabFunctionBlock('test_system/DualPendulum2', S.ddtheta2,... % theta2の2階微分を出力する演算ブロック作成
'vars',[I_1 I_2 L_1 M_1 M_2 c_1 c_2 g l_1 l_2 tau1 tau2 theta1 theta2 dtheta1 dtheta2],'outputs',{'ddtheta2'}) % 入力端子順序と出力端子名前を指示
(以下、しばしば画像中の変数記号にアンダーバーをつけたりつけなかったりしてますが、あまり気にしないでください。)
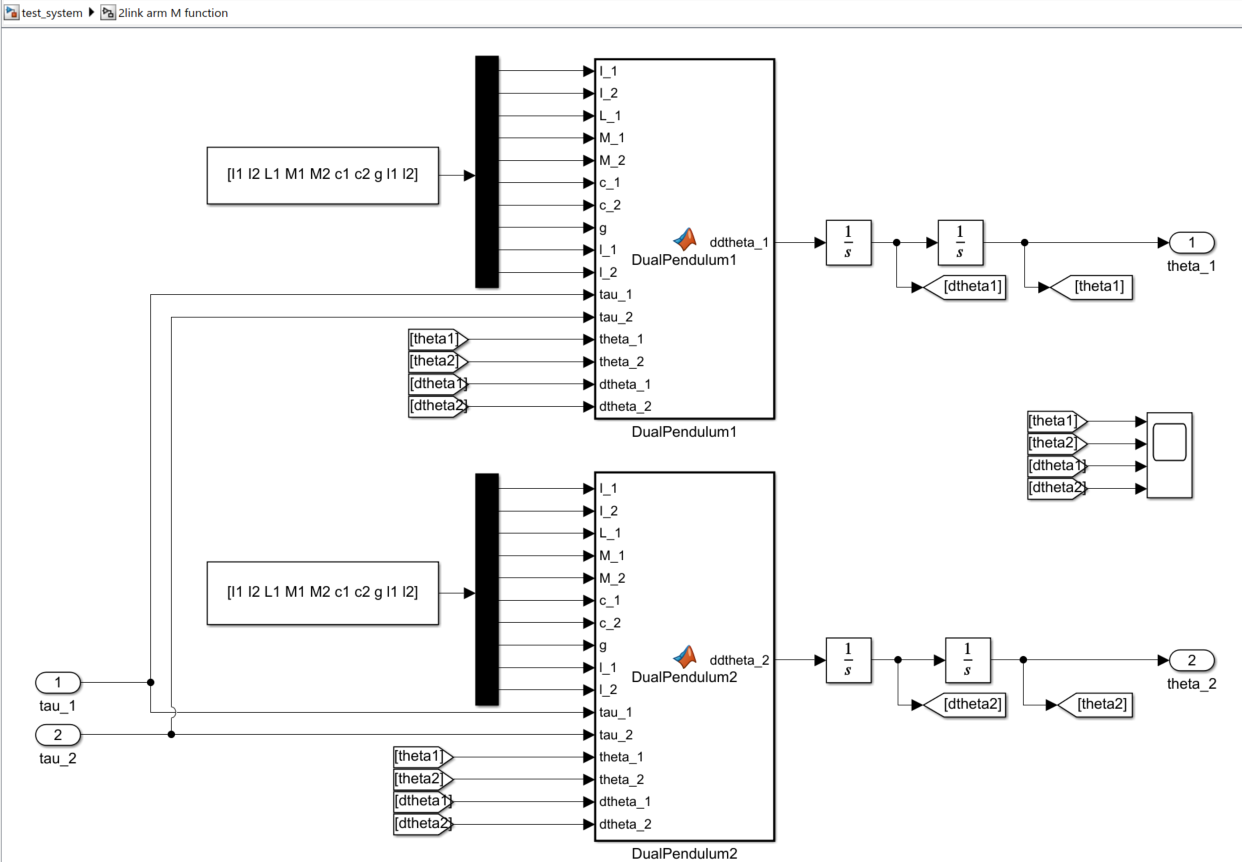
実行すると、test_systemというモデルが開かれ、下記のように2つのMATLAB Functionブロックが重なった状態で表示されます。

適当にサイズを調整し、必要な配線を行います。
- ddtheta1、ddtheta2は角加速度なので、2回Integratorブロックを挟んで角度にしていきます
- そのまま角度・角速度を両ブロックにつなぐとごちゃごちゃしそうなのでGotoブロック、Fromブロックを使って整理しています
- 長さ・重さ等々の物理パラメータはまとめてベクトル化してつないでます。param、とか名前を付けておいてもいいかもしれないです
- tau1、tau2はInport端子、theta1、theta2はOutport端子につないでサブシステム化しています。
ここで、自動で作られたMATLAB Functionブロックの中身をのぞいてみます。(MATLABはコードを勝手に折り返して表示してくれはしないので)適当なエディタで中身を眺めてみると、こんな感じです。非常に混沌としています。運動方程式の両辺に慣性行列の逆行列をかけた結果だと思いますが、2リンクでここまで複雑とは・・・という感じです。自分でこの入出力関係を求める気にはならないですね。
得られたモデルの動作確認
せっかくなので、手動で運動方程式を求め、Simulink上で各項目を自分で配置・配線してみた結果と比較しようと思います。
2リンクマニピュレータの運動方程式は下式となります。
\left(
\begin{array}{cc}
I_1 + I_2 + M_1 l_1^2 + M_2 L_1^2 + M_2 l_2^2 + 2 M_2 L_1 l_2 \cos(\theta_2) & I_2 + M_2 l_2^2 + M_2 L_1 l_2 \cos(\theta_2) \\
I_2 + M_2 l_2^2 + M_2 L_1 l_2 \cos(\theta_2) & I_2 + M_2 l_2^2
\end{array}
\right) \left(
\begin{array}{cc}
\ddot{\theta}_1 \\
\ddot{\theta}_2
\end{array}
\right)
= \left(
\begin{array}{cc}
M_2 L_1 l_2 (2 \dot{\theta_1} \dot{\theta_2} + \dot{\theta_2}^2) \sin(\theta_2) \\
-M_2 L_1 l_2 \dot{\theta_1}^2 \cos(\theta_2)
\end{array}
\right) -
\left(
\begin{array}{cc}
(M_1 l_1 + M_2 L_1) g \sin(\theta_1) - M_2 g l_2 \sin(\theta_1 + \theta_2) \\
M_2 g l_2 \sin(\theta_1 + \theta_2)
\end{array}
\right) -
\left(
\begin{array}{cc}
c_1 \dot{\theta}_1 \\
c_2 \dot{\theta}_2
\end{array}
\right) +
\left(
\begin{array}{cc}
\tau_1 \\
\tau_2
\end{array}
\right)
これをちまちま配線してSimulinkモデル化すると、下記のようになります。意外とそこまで複雑でもないですね。
慣性行列を$\theta_2$に関する行列、そうでない行列とでわけて、(演算上は良くないんでしょうが)Invで逆行列をかける形にしています。
この自分でブロックを配置したモデルと、先ほどのMATLAB Functionブロックでのモデルを並べて、結果を比較してみます。
適当に初期角度$\theta_1 = \pi/4$、$\tau_1 = 2$、$\tau_2 = 1$を印可してみました。
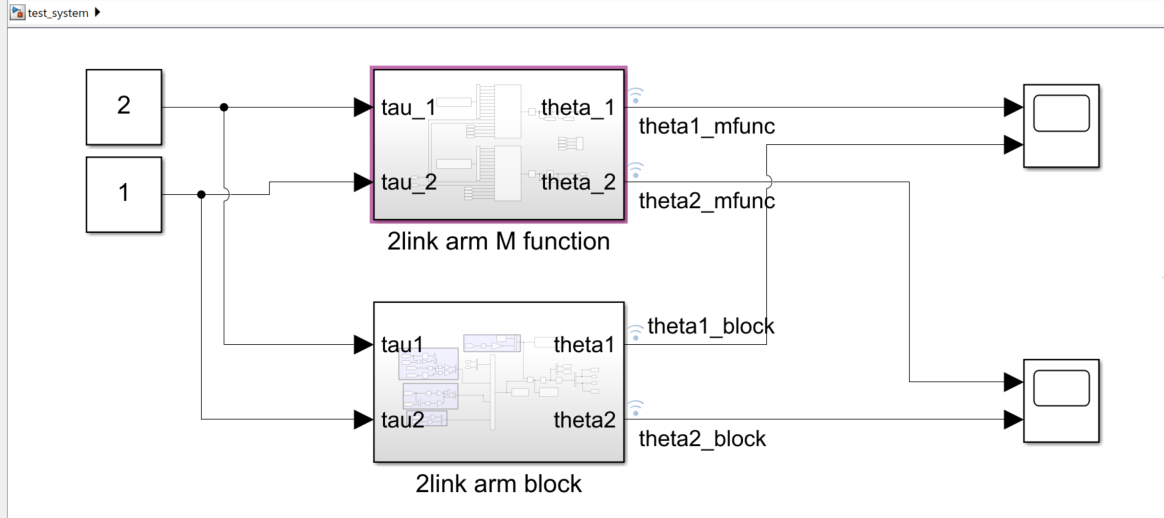
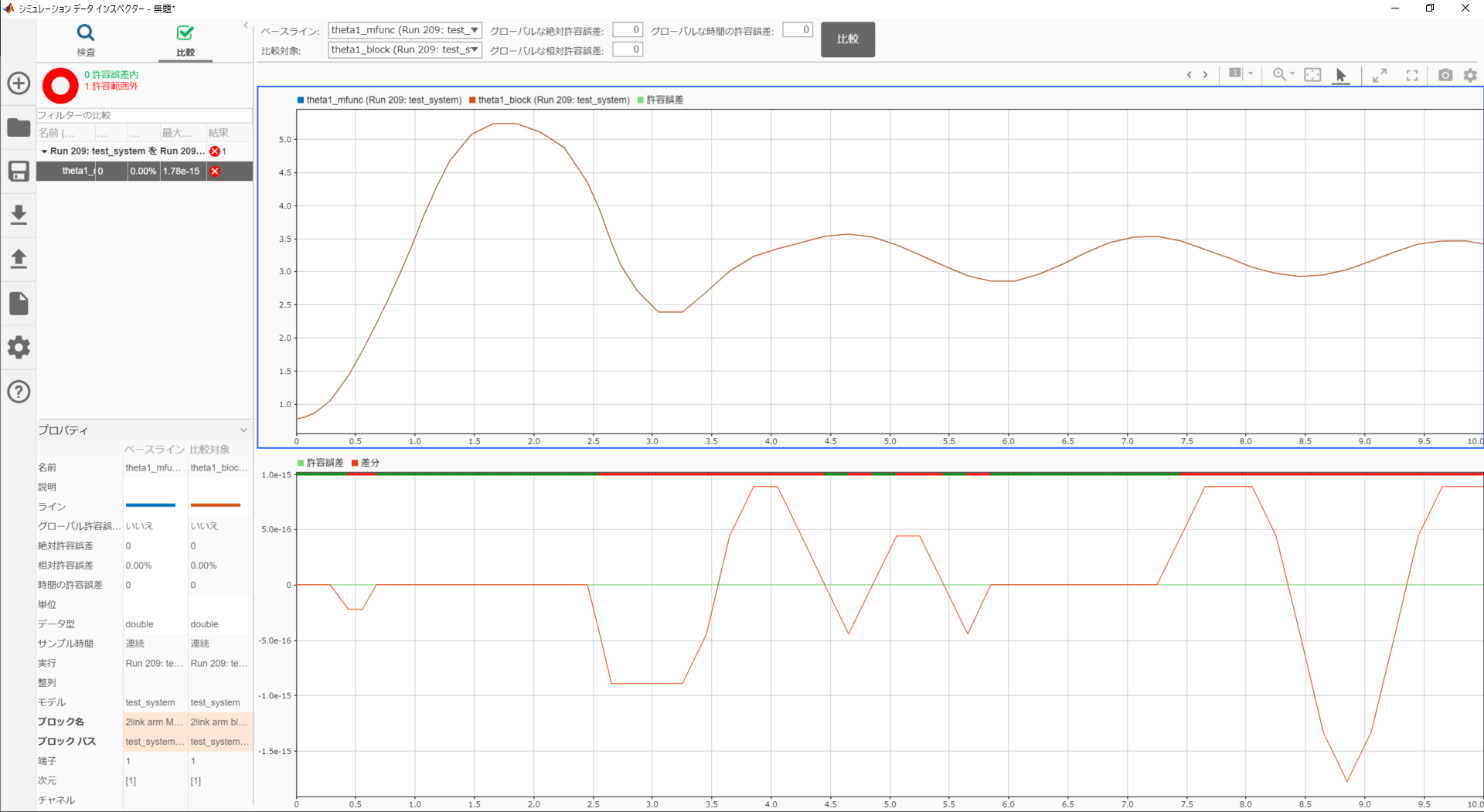
結果はシミュレーションデータインスペクターでサクッと確認していきます。下記の通り、両ブロックで生成した角度はほぼ同じような動きとなりました。

さらに、シミュレーションデータインスペクターでは、各項目の右クリック→信号の比較、で簡単に誤差が確認できます。

$\theta_2$の結果は下記のとおり、

でした。どちらも差は最大$10^{-15}$程度なので、どちらもほぼ全く同じ挙動をしているといえる結果となりました。
まったく異なったやり方で結果が合うと気分がいいですね!
2通りでの結果が合ったので、これで安心してこのモデルを使うことができそうです。
コードとモデル
MATLABコードとエクスポートしたモデル、それと比較に使ったモデルはこちら
おわりに
このモデルを使って制御工学に関する記事を書きました。そちらも見ていただければと思います。頑張って作ったモデルですが、その数理モデルをほとんど使わずに制御できる、という手法の紹介です。
なお、中身の運動方程式は気にせず動くマニピュレータモデルだけ欲しいのであれば、Simscape Multibodyで作ると簡単です。一応、参考ページを張っておきます。こちらをもとに2重振り子も簡単に作れます。それらに外部トルク入力を印可するのもお手軽です。
https://jp.mathworks.com/help/sm/gs/model-pendulum.html
それと比較したSymbolic Math Toolboxの良さとして、やはり「数式ベースの解析 → シミュレーションモデル生成or制御器モデル生成」が一気通貫でスムーズにできるところかなと思いました(今回の自分の用途ではあんまり活かせませんでしたが)。
その他、今回使ったSimulinkへのエクスポート機能に関して、思いつくところだと
- 制御対象のシミュレーションモデルは非線形なままで、制御器には線形近似したモデルを使う
- Matlab/Simulink しか持ってない人にモデルを渡す
- 中身を隠蔽したままモデルを渡す(さすがにこれは本来の使い方ではない??)
などのときに活躍しそうかなと思いました。
ちなみに、投稿直前にMATLAB Japanの素晴らしい動画を見つけました・・・。
本記事に興味を持たれた方は、下記も要チェックですね。今回、運動方程式をコード内で見やすく出力できなかったのが少し心残りなので、もし改善できたら更新しようと思います。
間違い・ご意見等あればコメントでお知らせください。ご覧いただきありがとうございました。