ABC 293 のA,B,C,D,E問題を解くために考えたこと、ACできるPython3(PyPy3)コードを紹介します。
この記事は @u2dayo さんの記事を参考にしています。見たことのない方はそちらもご覧ください。とても勉強になります。
また、問題の難易度を表す指標を Atcoder Problems から引用しています。このサイトは勉強した問題を管理するのにとてもオススメです。
質問やご指摘はこちらまで
Twitter : Waaa1471
作者プロフィール
Atcoder :緑 1014
230311 現在
目次
はじめに
A.Swap Odd and Even
B.Call the ID Number
C.Make Takahashi Happy
D.Tying Rope
E.Geometric Progression
はじめに
特にC問題以降になると、競技プログラミングに典型的な前提知識、少し難しい数学的考察が必要になり始めます。
しかし、公式解説ではこの部分の解説があっさりしすぎていて競技プログラミング(Atcoder)を始めたばかりの人にはわかりにくい、難しいと感じるのではないでしょうか。
またC++がわからないと、コードの書き方を勉強することが難しいです。一応、参加者全員のコードを見ること自体は可能ですが、提出コードは必ずしも教育的ではありません(ここで紹介する記事も本番で提出したものとは全く異なります)。そんなものから初学者が解説もなしになにか得ることはとても難しいと思います。実際適当に何人かのコードをみたものの、意味がわからずに終わった経験があるのではないでしょうか。
この記事がそんな方々の勉強の助けになればよいなと思っています。
A.Swap Odd and Even
難易度:灰色 12
考察
$S_{2i-1}\ ,\ S_{2i}\ $ の位置の文字の入れ替えを先頭から順に行います。
ただし、index 番号が 0 始まりであることに注意が必要です。$S_{0}\ ,\ S_{1}\ $ の入れ替えから始めるために、i および入れ替え位置を調整しなければいけません。
コード
pypy3
65 ms/2000 ms
S=input()
# 操作後の文字列
SS=""
# i は 0 始まり
for i in range(len(S)//2):
s1=S[2*i]
s2=S[2*i+1]
# 入れ替えた結果を結合
SS+=s2+s1
print(SS)
補足
- 文字列の結合
Pythonで文字列を連結・結合(+演算子、joinなど)
この問題のように単純に演算子を用いた結合だけでなく、配列から復元させることも可能です。結果自体は同じですが、実は計算量の観点では後者の方が優れています。($\ O(n^2)\ vs\ O(n)\ $ )
B.Call the ID Number
難易度: 灰色 65
考察
人 i を呼んだ際にその人が既に呼ばれているかによって、人 Ai を呼ぶかが決定します。
したがって、各人それぞれが呼ばれているかテーブルで管理してこれを判定していきます。一度も呼ばれたことのない人を抽出する際にも、この状態配列が利用できます。
なお、出力形式は空白区切りで、番号は 1 始まりであることに注意します。
コード
pypy3
N=int(input())
A=[int(a)-1 for a in input().split()]
# 呼ばれたかを管理
seen=[False for _ in range(N)]
for i,a in enumerate(A):
# 呼ばれてなければ Ai を呼ぶ
if not seen[i]:
seen[a]=True
ans=0
# 一度も呼ばれていない人間を格納
table=[]
for i in range(N):
if seen[i]:
continue
ans+=1
# 1-indexed
table.append(i+1)
print(ans)
print(*table)
補足
- 出力形式
競技プログラミングにおける Python での標準入出力のまとめ
出力形式を勉強するのに便利です。
C.Make Takahashi Happy
難易度 : 茶色 431
考察
(1,1) から (H,W) までの経路全てを深さ優先探索で調べることもできますが、制約から盤(マス目)はとても狭いので経路を全列挙できそうだと考えました。
実際経路は 右移動 W-1 回 と 下移動 H-1 回の並び方で表現できるので、18C9 個程度しかありません。これらの経路の内条件を満たすものの個数を計上すればよいです。
ただし組み合わせから経路を復元することは難しいので、実装では代わりに18桁の2進数で経路を列挙します。各桁の数字で進行方向が表現されるので復元が簡単です。いわゆる bit 全探索です。
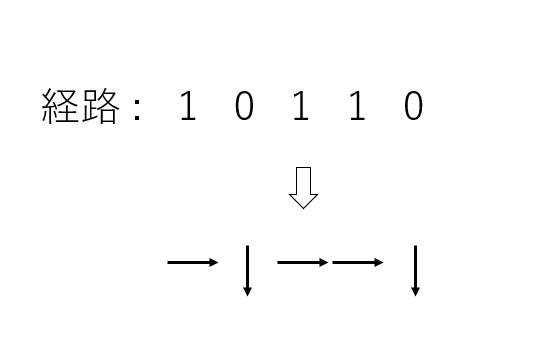
組み合わせでの表現よりも、ありえない経路を含む分計算量が多いですがこれでも十分高速です。
コード
pypy3
229 ms/2000 ms
H,W=[int(hw) for hw in input().split()]
HW=[]
for _ in range(H):
A=[int(a) for a in input().split()]
HW.append(A)
ans=0
# 経路全列挙
for order in range(2**(H+W-2)):
h,w=0,0
# マスの種類を管理
seen=set()
seen.add(HW[0][0])
# i 番目のマス ( order(2) の i 桁目 )
for i in range(H+W-2):
if order>>i & 1:
h+=1
# 盤外
if h==H:
break
# 嬉しくない
if HW[h][w] in seen:
break
else:
w+=1
# 盤外
if w==W:
break
# 嬉しくない
if HW[h][w] in seen:
break
# マスを記録
seen.add(HW[h][w])
# 条件を満たす経路なら計上
else:
ans+=1
print(ans)
補足
-
全列挙 (bit 全探索)
こわくないbit全探索1 入門編: bit全探索ってなに?【競プロ解説】
教科書として最適です。 -
全列挙 (bit 全探索) 類題
類題ページ
ネタバレ回避で abc 285 ~ 290 の c または d と記載します。
この問題も記事にしているので、解答後見てみてください -
bit 演算
Pythonのビット演算子(論理積、論理和、排他的論理和、反転、シフト)
bit シフトをはじめ、なにかと利用機会は多いので理解しておきましょう
D.Tying Rope
難易度: 緑色 830
考察
まずロープを結ぶことを、各ロープを表現する頂点どうしに辺を張る(構築する)こと と解釈できます。この問題では一度結ばれた端が再度結ばれる(呼ばれる)ことも、一つのロープの端同士で結ばれることもありません。したがって 頂点に色の情報を持たせる必要は全くありません。「 色の影響で結ぶことができない 」などの問題が一切生じないからです。
既に(直接でなくても)結ばれているふたつのロープが結ばれることで、それらは環状にひとつながりになります。
つまりロープを結んでグループを形成し、環状に結ばれる(閉路を成す)グループを計上することが求められています。これはもう union-find でデータを管理するのが良いでしょう。
閉路はその閉路ができる瞬間に計上すればよいです。この閉路はこれ以降閉路を成すことはないので、再計上を心配する必要はありません。
Y = 全操作終了後にできたグループの数 - 閉路数(X) が成立するので、これを求めて出力します。
コード
pypy3
452 ms/2000 ms
メイン
ここに union-find クラスを書く
if __name__ =="__main__":
N,M=[int(nm) for nm in input().split()]
uf=UnionFind(N)
x=0
for _ in range(M):
a,b,c,d=input().split()
a,c=int(a)-1,int(c)-1
if uf.same(a,c):
x+=1
uf.union(a,c)
y=0
for i in range(N):
# グループ数
if uf.parents[i]<0:
y+=1
print(x,y-x)
union-find クラス
class UnionFind():
def __init__(self,n):
self.n = n
self.parents = [-1] * n
def find(self,x):
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self,x,y):
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def same(self,x,y):
return self.find(x) == self.find(y)
補足
- union-find クラス
PythonでのUnion-Find(素集合データ構造)の実装と使い方
筆者もここで勉強して union-find の各関数を理会しました。とても分かりやすいのでお勧めです。
B - Union Find
スライドがとてつもなく分かりやすく、操作を視覚的に理解できます。
アルゴ式
理解できたら練習あるのみです。出題傾向が高く、実装も簡単で得点源となるアルゴリズムです。わからない人は今すぐ勉強しておきましょう。
E.Geometric Progression
問題ページ
難易度 : 水色 1453
考察
\begin{align}
\sum_{i=1}^{X-1}\ A^i =\ \frac{A^X-1}{A-1}
\end{align}
「 初項 1 公比 A の等比数列における n 項の総和 」と解釈すれば上の等式の成立を理解できます。
もし「 M が素数 」 かつ「 A と M が互いに素 」であれば、フェルマーの小定理から逆元を求めることができるのですが、この問題ではこれらの条件を満たしているとは限りません。
このような条件下では以下の ➁ で示す理由で $\ mod\ (\ A\ -\ 1\ ) × M$ をとればよいです。
コード
pypy3
64 ms/2000 ms
公式解説 5 に対応
A,X,M=[int(axy) for axy in input().split()]
# 分母 0 を例外処理
if A==1:
print(X%M)
exit()
# mod 変換
MOD=(A-1)*M
Ax=pow(A,X,MOD)
# 分子計算
b=(Ax-1)%MOD
ans=b//(A-1)
print(ans)
別解 遷移状態を限定
$f(k)$ : 公比 A の等差数列の k 項目までの総和 (mod M) とすると、状態は以下のように遷移することが分かります。
f(k+1) = Af(k) + 1
このように $f(1) = 1 \ から順に\ f(X)$ まで求めていくことは理論的には可能ですが、X が非常に大きいため制限時間内で解答することができません。
そこで、考える(遷移させる)状態を限定して、少ない計算回数で最終状態を求めることを目指します。
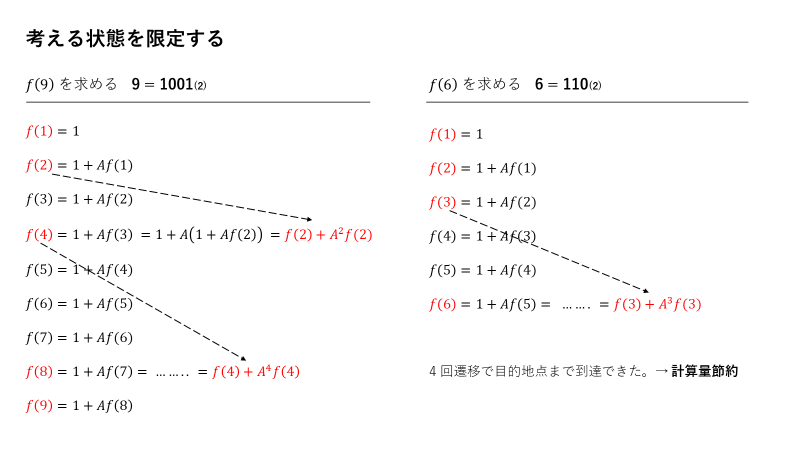
このように基本的には、$2^k$ ごとに遷移し必要に応じて調整することで、$O(logX)$ (X の2進数表示桁数) 程度でどんな状態でも求めることが可能です。
$f(6)$ を求めるならば、6=110(2) より、$f(1(2)) → f(10(2)) → f(11(2)) → f(110(2))$ と遷移させることになります。つまり X(2) の各桁にある 1 で遷移を調整します。
コード
pypy3
71 ms/2000 ms
公式解説 3 に対応
A,X,M=[int(axm) for axm in input().split()]
# 2進数表示
X=f"{X:b}"
L=len(X)
# 初項も余りで作成しておく
now=1%M
k=1
for i in range(1,L):
now=now*(pow(A,k,M))+now
now%=M
k*=2
if X[i]=="1":
now=now*A+1
now%=M
k+=1
print(now)
補足
-
等比数列の mod
mod Nで等差数列/等比数列の和を計算 -
フェルマーの小定理と逆元
・フェルマーの小定理の証明と例題
・「1000000007 で割ったあまり」の求め方を総特集! 〜 逆元から離散対数まで 〜
この問題は特殊で、むしろ分数の素数 mod を問う問題が頻出です。
終わり
また見てくれよな!
