ABC 291 のA,B,C,D,E 問題を解くために考えたこと、ACできるPython3(PyPy3)コードを紹介します。
この記事は @u2dayo さんの記事を参考にしています。見たことのない方はそちらもご覧ください。とても勉強になります。
また、問題の難易度を表す指標を Atcoder Problems から引用しています。このサイトは勉強した問題を管理するのにとてもオススメです。
質問やご指摘はこちらまで
Twitter : Waaa1471
作者プロフィール
Atcoder :緑 944
230227 現在
目次
はじめに
A.camel Case
B.Trimmed Mean
C.LRUD Instructions 2
D.Flip Cards
E.Find Permutation
はじめに
特にC問題以降になると、競技プログラミングに典型的な前提知識、少し難しい数学的考察が必要になり始めます。
しかし、公式解説ではこの部分の解説があっさりしすぎていて競技プログラミング(Atcoder)を始めたばかりの人にはわかりにくい、難しいと感じるのではないでしょうか。
またC++がわからないと、コードの書き方を勉強することが難しいです。一応、参加者全員のコードを見ること自体は可能ですが、提出コードは必ずしも教育的ではありません(ここで紹介する記事も本番で提出したものとは全く異なります)。そんなものから初学者が解説もなしになにか得ることはとても難しいと思います。実際適当に何人かのコードをみたものの、意味がわからずに終わった経験があるのではないでしょうか。
この記事がそんな方々の勉強の助けになればよいなと思っています。
A.camel Case
難易度: 灰色 8
考察
入力文字列 S に含まれる唯一の大文字の位置を求めるためには、S の先頭から順に大文字が検出できるまで調べていけばよいでしょう。python では isupper() 関数で文字列の大文字判定が可能です。
ただし、S に含まれる文字の位置は 1 始まりであるのに対して、index番号から求めた位置は 0 始まりです。したがって、出力時にこのズレを調整する必要があります。
コード
pypy3
96 ms/2000 ms
S=input()
for i,s in enumerate(S):
if s.isupper():
print(i+1)
補足
-
enumerate() 関数
Python, enumerateの使い方: リストの要素とインデックスを取得
文字列、イテラブル(リストなど)から要素とその位置を同時に取得したいときに利用します。 -
文字列の大文字、小文字判定
Pythonで大文字・小文字を操作する文字列メソッド一覧
B.Trimmed Mean
難易度:灰色 32
考察
昇順に点数を並べたときの前から N+1 番目 ~ 4N 番目までの計 3N 個の平均点を求めればよいです。
そのために、まず該当する点数のみを抽出します。入力の数列 X をソートして、[ N : 4N ] の範囲でスライスすればこれを実行できます。
後は全要素を足し合わせて 3N で割れば目的の平均点が得られます。
index 番号が 0 始まりであること、[ a : b ] の範囲でスライスすると a ~ b-1 の位置が抽出されることに気を付けます。
コード
pypy3
69 ms/2000 ms
N=int(input())
# 昇順にソートして、N+1 ~ 4N 番目までを抽出
X=sorted([int(x) for x in input().split()])[N:4*N]
ans=0
for x in X:
ans+=x
print(ans/(3*N))
補足
C.LRUD Instructions 2
難易度 : 灰色 188
考察
過去到達したことのある全ての座標 を管理しておけば、「 現在地に一度でも訪れたことがあるか 」を「 現在地がこれに含まれるか 」で判定できるようになります。
ただし、全体で N 回判定を行うことになるので 1度の判定を高速に行う必要があります。 そこで、過去到達したことのある全ての座標を 集合 で管理します。集合であれば要素検索を $O(1)$ で行えるためです。
注意点としては、座標 x , y は hashable (ハッシュ可能) なオブジェクトであるタプル型の ( x,y ) の形で集合に格納します。リスト型の [ x,y ] の形で格納することはできません。
コード
pypy3
123 ms/ 2000ms
N=int(input())
S=input()
# 現在位置
x,y=0,0
# 既出位置を管理
X=set()
X.add((0,0))
for s in S:
if s=="R":
x+=1
if s=="L":
x-=1
if s=="U":
y+=1
if s=="D":
y-=1
if (x,y) in X:
print("Yes")
exit()
X.add((x,y))
print("No")
補足
-
計算量
Pythonistaなら知っておきたい計算量のはなし
リスト内要素検索では $O(k)$ かかってしまう点など覚えておきましょう -
hashable
公式ドキュメント hashable 項目
辞書や集合の要素は hashable でなければなりません。
D.Flip Cards
難易度: 茶色 720
考察
カードの並べ方を前から順に決定する場合 i 番目のカードの置き方は i-1 番目のカードの値にのみ依存します。したがって
$dp[\ i\ ][\ x\ ]$ : $i$ 番目のカードの値が $x$ となる置き方の総数
で状態を定義することで、以下のように遷移に忠実に全状態を決定することができます(動的計画法)。
$dp[\ i\ ][\ x\ ]$ += $dp[\ i-1\ ][\ x\ 以外\ ]$
計算量
遷移数は定数回なので計算量は全体で $O(N × max(max(A),max(B)))$ となります。
$ A,B ≦ 10^9 $ より、このままでは間に合わないことがわかります。
ボトルネックは管理すべき状態が多すぎることです。どうにかしてカードの値よりも種類が少ない「 何か 」で状態を定義することができないでしょうか。
そこで、カードの値を「 番号 」と「 置き方 」 に紐づけて記憶し、置き方からカードの値を取得可能とすることで、カードの値の代わりに「 置き方 」で状態を定義できるようにします。
つまり i 番目の置き方が j ( 表 or 裏 ) となるカードの値を管理するテーブル : $AB[\ i\ ][\ j\ ]$ を作成し、i 番目のカードの置き方が j ( 表 or 裏 ) となる置き方の総数 : $dp[\ i\ ][\ j\ ]$ で状態を定義し直します。
これにより状態数は 2N となるため、計算量は全体で $O(N)$ に改善されました。
コード
pypy3
381 ms /2000ms
N=int(input())
AB=[]
for _ in range(N):
a,b=[int(ab) for ab in input().split()]
AB.append([a,b])
MOD=998244353
dp=[[0,0] for _ in range(N)]
dp[0][0]=1
dp[0][1]=1
for i in range(1,N):
for j in range(2):
if dp[i-1][j]:
for k in range(2):
if AB[i-1][j]!=AB[i][k]:
dp[i][k]+=dp[i-1][j]
dp[i][k]%=MOD
print((dp[-1][0]+dp[-1][1])%MOD)
補足
- 動的計画法 ( DP )
・動的計画法ってなに? (導入)
・典型的な DP (動的計画法) のパターンを整理 Part 1 ~ ナップサック DP 編 ~
こちらで動的計画法の概念を勉強することができます。
分かるようになったら、アルゴ式 1~2章で練習してみましょう
動的計画法 ( DP )
E.Find Permutation
問題ページ
難易度 : 緑色 1069
考察
A は順列であるので $A_1 < A_2 < ... < A_n$ のとき、$A_1 =1 , A_2 = 2 .... , A_n = N$ と決定できます。
したがって、「 A を一意に特定すること 」と「 A の要素の大小関係を一意に特定すること 」は同値であることがわかります。
ここで、A の要素間の大小関係は X , Y によって、$A_{X} < A_{Y}$ と決定されますが、$これを\ A_{X} ← A_{Y}\ 、つまり「\ 頂点\ A_Y から頂点\ A_X$ に有向辺を張ること 」と解釈します。なぜなら、「 こうして構築した有向グラフの頂点を入次数順に探索した順番 」と 「 A の要素の大小関係 」 とが一致する かつ、前者はトポロジカルソートで求めることができるからです。
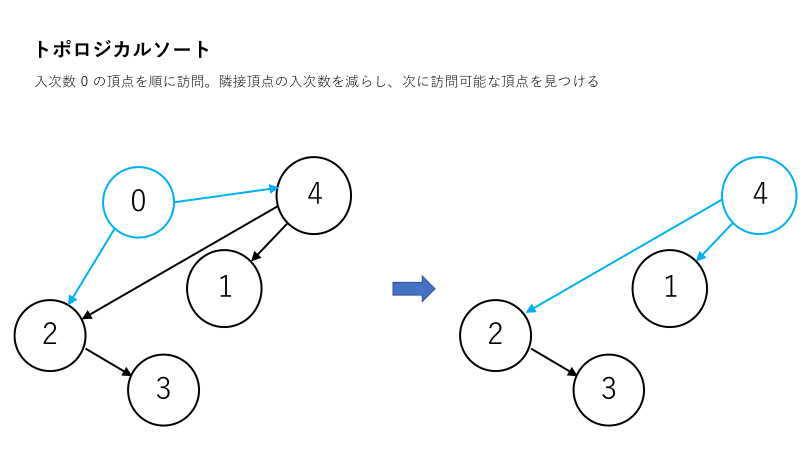
以上より、この問題は「 A の要素をトポロジカルソートして並び替えた順番が一意に定まるか 」判定する問題であると解釈することができました。
「 A の順番が一意に定まること」と 「 常に、同時に複数の頂点を探索できないこと 」が同値であることに注目すると、探索中、現在何個の頂点を同時に探索可能であるか管理すれば、この問題を判定できるとわかります。
コード
pypy3
478 ms/2000 ms
from collections import deque
N,M=[int(nm) for nm in input().split()]
que=deque()
# 有向グラフ
G=[[] for _ in range(N)]
# 入次数
table=[0 for _ in range(N)]
for _ in range(M):
x,y=[int(xy)-1 for xy in input().split()]
G[y].append(x)
table[x]+=1
# 探索可能頂点数
tmp=0
for i in range(N):
if table[i]==0:
tmp+=1
que.append(i)
if tmp!=1:
print("No")
exit()
order=[0 for _ in range(N)]
rem=N
while True:
now=que.popleft()
tmp-=1
order[now]=rem
rem-=1
# 全位置を決定できたら終了
if rem==0:
break
for nex in G[now]:
table[nex]-=1
if table[nex]==0:
que.append(nex)
tmp+=1
if tmp!=1:
print("No")
exit()
print("Yes")
print(*order)
補足
-
トポロジカルソート
トポロジカルソートのアルゴリズム(閉路のない有向グラフDAGのソート)※ 個人的にアルゴ式の例題は教育的でないのでオススメしません。
この問題やこちらの類題で練習すればよいと思います。
念のためネタバレ防止で、abc 220 ~ 225 の c or d と記します。
終わり
また見てくれよな !!!