【Pyro】確率的プログラミング言語Pyroによる統計モデリング③ ~分散分析モデル, 正規線形モデル~

はじめに

前々回・前回の記事で，確率的プログラミング言語Pyroの基本的な使い方と，Pyroで単回帰モデルのパラメタをベイズ推論する方法を紹介しました．今回は，参考書籍の第3部6章に登場する「分散分析モデル」，7章に登場する「正規線形モデル」をPyroで実現する方法を紹介します．

分散分析モデル

利用データ & 例題紹介

前回の記事と同様に，今回扱うデータもビールの売り上げに関するものです．前回は説明変数が気温でしたが，今回は説明変数が 天気 です．

	sales	weather
0	48.5	cloudy
1	64.8	cloudy
2	85.8	cloudy
3	45	cloudy
4	60.8	cloudy

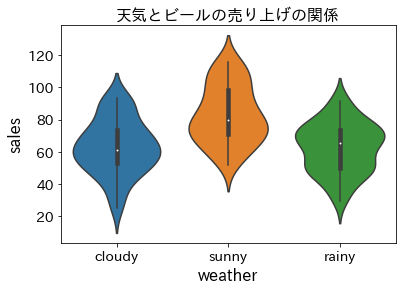天気という質的変数を説明変数とし，ビールの売り上げを説明するモデルとして，分散分析モデルを用います．参考書籍では以下のように説明されています．

応答変数の平均値が天気によって変化すると想定したモデルです．説明変数に質的データを用いて確率分布に正規分布を仮定したモデルを分散分析モデルと呼びます．

(馬場真哉. 実践Ｄａｔａ　Ｓｃｉｅｎｃｅシリーズ　ＲとＳｔａｎではじめる　ベイズ統計モデリングによるデータ分析入門 (Japanese Edition) (Kindle の位置No.3608-3610). Kindle 版. )

この問題では天気が {sunny, rainy, cloudy} の３種類あるので，晴れを表すダミー変数($\it{sunny}$)と，雨を表すダミー変数($\it{rainy}$)を組み込み，以下のようなモデルとなります．潜在変数($Intercept, \beta_1, \beta_2, sigma^2$)を推定していきます．

$sales_i \sim \rm{Normal}(Intercept + \beta_1\it{sunny_i} + \beta_2\it{rainy}_i , sigma^2)$

実装

以下では，MCMCによる事後分布の推定を行う実装を示します．

import pyro
import pyro.distributions as dist
import pyro.infer as infer


def model(sunny: torch.Tensor, rainy: torch.Tensor, sales: torch.Tensor=None):
    intercept = pyro.sample("intercept", dist.Normal(0, 1000))
    beta1 = pyro.sample("beta1", dist.Normal(0, 1000))
    beta2 = pyro.sample("beta2", dist.Normal(0, 1000))
    sigma2 = pyro.sample("sigma2", dist.Uniform(0, 1000))
    with pyro.plate("plate", size=sunny.size(0)):
        y_ = intercept + beta1 * sunny + beta2 * rainy
        y = pyro.sample("y", dist.Normal(y_, sigma2), obs=sales)
    return y

# データ読み込み
beer_sales_3 = pd.read_csv('https://github.com/logics-of-blue/book-r-stan-bayesian-model-intro/raw/master/book-data/3-6-1-beer-sales-3.csv')
# ダミー変数化
rainy_sunny = pd.get_dummies(beer_sales_3.weather, drop_first=True)
sunny = torch.Tensor(rainy_sunny.sunny)
rainy = torch.Tensor(rainy_sunny.rainy)
sales = torch.Tensor(beer_sales_3.sales)

# MCMCによる事後分布の推定
nuts_kernel = infer.NUTS(model, adapt_step_size=True, jit_compile=True, ignore_jit_warnings=True)
mcmc = infer.MCMC(nuts_kernel, num_samples=5000, warmup_steps=200, num_chains=1)
mcmc.run(sunny, rainy, sales)
mcmc.summary()

	mean	std	median	5.0%	95.0%	n_eff	r_hat
intercept	63.06	2.4	9.03	59.12	67	2435.11	1
beta1	20.02	3.39	9.03	14.12	25.27	2729.79	1
beta2	-0.36	3.34	9.03	-5.43	5.42	2716.48	1
sigma2	16.95	0.97	16.91	15.25	18.42	3628.93	1

書籍での結果と一致していることがわかります．$beta_1$の95%信頼区間が14.12 ~ 25.27となっていることから，天気が晴れだと曇りのときと比べて売上が上がる傾向にあることがわかります．一方，$beta_2$の信頼区間は0を跨いでいることから，雨が降っている場合は曇りの場合と比べ大きな違いがないということがわかります．

正規線形モデル

利用データ & 例題紹介

単回帰モデルでは売上を気温で説明するモデル，分散分析モデルでは売上を天気で説明するモデルを仮定しました．これまでのモデリングの結果から，気温も天気もそれぞれ売上と関係がある要素であることがわかりました． ここでは，売上を説明するために，気温という量的変数と，天気という質的変数の両方を組み込んだモデルを構築することを考えます．このような状況で用いられるのが，正規線形モデルです．
参考書籍による説明は以下の通りです．

量的データや質的データを問わず，複数の説明変数が線形予測子に用いられ，恒等関数がリンク関数であり，正規分布を確率分布に用いるモデルは総じて正規線形モデルと呼ばれます．

モデルを式で記述すると以下の通りです．潜在変数($Intercept, \beta_1, \beta_2, \beta_3, sigma^2$)を推定します．

$sales_i \sim \rm{Normal}(Intercept + \beta_1\it{sunny_i} + \beta_2\it{rainy_i} + \beta_3\it{temperature_i}, sigma^2)$

	sales	weather	temperature
0	40.6433	cloudy	13.7
1	99.5527	cloudy	24
2	85.3268	cloudy	21.5
3	69.2879	cloudy	13.4
4	71.0994	cloudy	28.9

実装

import pyro
import pyro.distributions as dist
import pyro.infer as infer


def model(sunny: torch.Tensor, rainy: torch.Tensor, temperature: torch.Tensor, sales: torch.Tensor=None):
    intercept = pyro.sample("intercept", dist.Normal(0, 1000))
    beta1 = pyro.sample("beta1", dist.Normal(0, 1000))
    beta2 = pyro.sample("beta2", dist.Normal(0, 1000))
    beta3 = pyro.sample("beta3", dist.Normal(0, 1000))
    sigma2 = pyro.sample("sigma2", dist.Uniform(0, 1000))
    with pyro.plate("plate", size=sunny.size(0)):
        y_ = intercept + beta1 * sunny + beta2 * rainy + beta3 * temperature
        y = pyro.sample("y", dist.Normal(y_, sigma2), obs=sales)
    return y

# データ読み込み
beer_sales_4 = pd.read_csv('https://github.com/logics-of-blue/book-r-stan-bayesian-model-intro/raw/master/book-data/3-7-1-beer-sales-4.csv')
# データ変形
rainy_sunny = pd.get_dummies(beer_sales_4.weather, drop_first=True)
sunny = torch.Tensor(rainy_sunny.sunny)
rainy = torch.Tensor(rainy_sunny.rainy)
temperature = torch.Tensor(beer_sales_4.temperature)
sales = torch.Tensor(beer_sales_4.sales)
# 変分推論による推定
guide = infer.autoguide.guides.AutoDelta(model)
adam_params = {"lr": 1e-1, "betas": (0.95, 0.999)}
oprimizer = pyro.optim.Adam(adam_params)

svi = infer.SVI(model, guide, oprimizer, loss=infer.JitTrace_ELBO(),)

n_steps = 100000
losses = []
param_dict = defaultdict(list)
for step in tqdm(range(n_steps)):
    loss = svi.step(sunny, rainy, temperature ,sales,)
    update_param_dict(param_dict)
    losses.append(loss)

# 推定結果の表示
for name in pyro.get_param_store():
    print("{}: {}".format(name, pyro.param(name)))

AutoDelta.intercept: 20.227853775024414
AutoDelta.beta1: 29.45983123779297
AutoDelta.beta2: -3.535917043685913
AutoDelta.beta3: 2.547081708908081
AutoDelta.sigma2: 15.715911865234375

切片が約20.2，$beta_1$が約29.5，$beta_2$が約-3.54，$beta_3$が約2.55となり，参考書籍でのMCMCでの推定結果と一致することがわかります．

まとめ

前回および今回の記事で，応答変数に正規分布を仮定した線形回帰モデル(単回帰モデル,分散分析モデル, 正規線形モデル)をPyroで実現する方法について紹介してきました．
次回からは，応答変数の分布にポアソン分布を仮定したポアソン回帰モデルによるモデリングをPyroで実現する方法を紹介していきます．