私がZennで記事にしていた内容の転写です。
はじめに
このスクリプトは統計検定準1級の合格に向けた最尤法の理解を補助するために記載されています。したがって最尤法の本質そのものを記載しているわけではなく、あくまで理解に向けての序論にについて記載しています。なお、統計検定2級を合格されている方だとより理解が進むスクリプトとなっています。
最尤とは
おそらく統計学を学び始めて初めて知る日本語だと思います。最尤(さいゆう)と読み、噛み砕くと「最も尤(もっと)もらしい」となります。仰々しい書き方をすると「観測データが与えられたとき、そのデータが最も尤もらしく(最も可能性が高く)生成されるようなパラメータを推定する」ということになります。
"パラメータを推定"と聞くと、統計検定2級合格者は区間推定が頭に浮かびますが、最尤法では点推定に関して用いられる用語になります。
2級の範囲だと点推定で関連する内容としては、サンプル数$n$における平均$\bar{x}$は$n$を大きくすると母集団の$µ$と等しくなる、という性質がある、なんて覚えている人もいるかと思います。しかし最尤法という考えは、単に母集団の平均や分散を標本で推定するだけではなく、より広範な応用を持っています。
最尤法を考える前のイメージの話
最尤法について理解するためには、まず最尤法という言葉自体の難解さをときほぐす必要があります。次の問から理解をはじめます。
袋の中に無限個の玉が入っていて、赤玉と白玉が入っている。その中から10個の玉を取り出した際、赤球が3個、白球が7個だった。この時の袋の中の赤球の割合$p$を点推定せよ。
まずサンプルである10個について理解を始めます。
赤玉と白玉が入っていてその中から赤玉の割合$p$を求めるわけですから、二項分布を適用できます。二項分布の公式からサンプル結果は次のように記載できます。
{}_{10}C_{3} p^3 (1-p)^7
$p$はまだわからないので、ひとつひとつ当てはめて確率がどのように変化するのかPythonの計算で見てみます。
import math as mt
# from scipy.stats import binom # 理解のためにbinomは使わずに計算します
# p=1/10のとき
mt.comb(10,3) * (1/10)**3 * (9/10)**7
0.05739562800000002
# p=2/10のとき
mt.comb(10,3) * (2/10)**3 * (8/10)**7
0.2013265920000001
result = []
for i in range(3,11):
result.append(mt.comb(10,3) * (i/10)**3 * ((10-i)/10)**7)
print(result)
[0.2668279319999998, 0.21499084799999998, 0.1171875, 0.042467328000000006, 0.009001691999999995, 0.0007864320000000004, 8.748000000000005e-06, 0.0]
以上から、袋から10個抜き出すと赤玉3個白玉7個だった事実から袋の中に無限個ある赤玉と白玉に関して、袋の中の赤玉の割合$p$は$3/10$が確率が最も高い結果となりました。つまり、この問いにおける袋の中の赤玉の割合は$3/10$が尤もらしい値であるということになります。ちなみに$P=10/10$の確率が0となった理由は、白玉が存在していることが確定の事実だからです。
イメージの一般化
イメージでは二項分布で考え、かつ10個という少ないサンプル数でした。では赤玉が4個だった場合や7個だった場合はどうでしょうか。あるいは今回の例は二項分布でしたが指数分布(連続的な分布)でサンプル数が3000とか多い場合はどうでしょう。ひとつひとつ確認するのはとても煩雑です。ですのでイメージを一般化しましょう、という話に移ります。
一般化する前に、さきほどのイメージをグラフで表してみます。
import math as mt
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
result = []
n = 10
k = 3
success_probabilities = np.linspace(0.0,1.0,11)
for i in success_probabilities:
x = binom.pmf(k,n,i)
result.append(x)
print(result)
plt.plot(success_probabilities, result, marker='o')
plt.title('Binomial PMF for Different Success Probabilities')
plt.xlabel('Success Probability')
plt.ylabel('Probability of 3 Successes')
plt.grid(True)
plt.savefig('binomial_pmf.png', format='png')
plt.show()
[0.0, 0.05739562799999998, 0.20132659199999992, 0.266827932, 0.21499084799999976, 0.1171875, 0.042467327999999964, 0.009001691999999985, 0.0007864319999999988, 8.747999999999991e-06, 0.0]
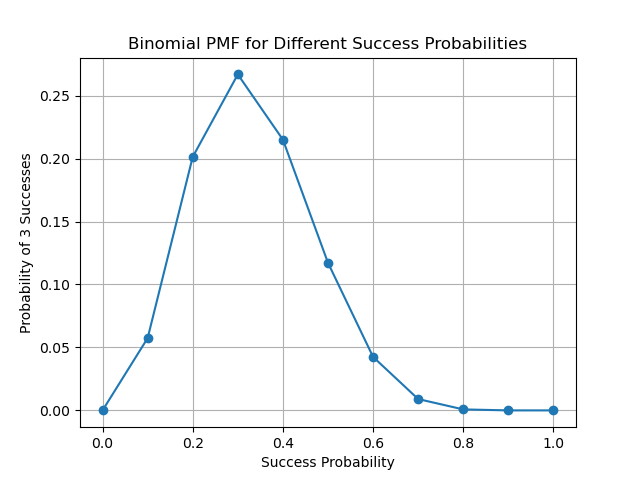
これを見ると、$p=(3/10)$で間違いなく最大値をとっています。確かに赤玉が3つでたときの袋の中の赤玉が入っている割合は$p=(3/10)$が尤もらしいと言えそうです。
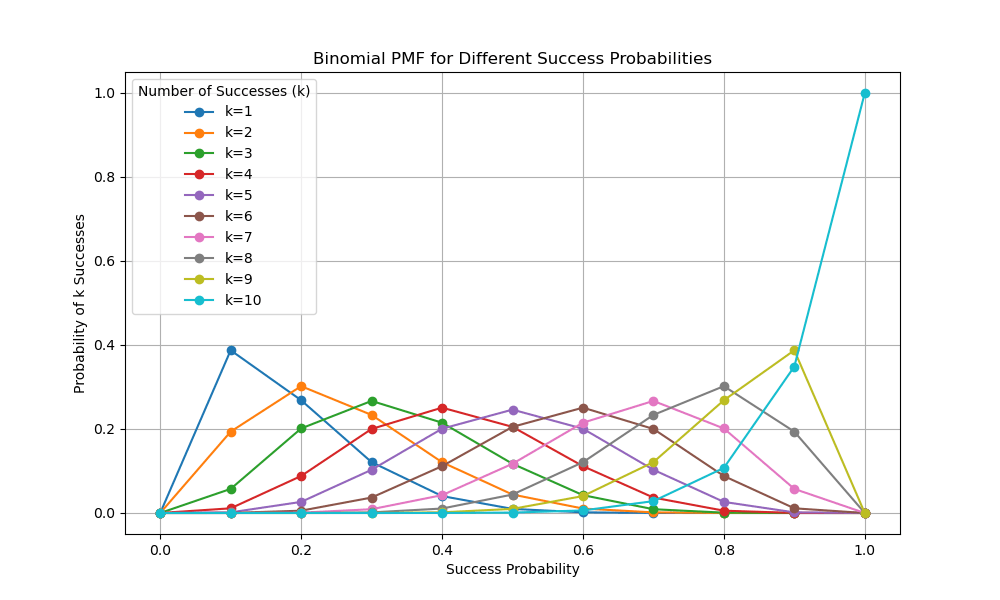
では10個の中に赤玉がk個(k=1,2,...,10)入っていた場合の尤もらしい$p$を考えてみましょう。
n = 10
success_probabilities = np.linspace(0.0, 1.0, 11)
plt.figure(figsize=(10, 6))
for k in range(1, 11):
result = []
for p in success_probabilities:
prob = binom.pmf(k, n, p)
result.append(prob)
plt.plot(success_probabilities, result, marker='o', label=f'k={k}')
plt.title('Binomial PMF for Different Success Probabilities')
plt.xlabel('Success Probability')
plt.ylabel('Probability of k Successes')
plt.grid(True)
plt.legend(title='Number of Successes (k)')
plt.savefig('binomial_pmf_k.png', format='png')
plt.show()
いずれの結果でも、尤もらしい値は各条件における最大値を示すことになります。
この状態を数学的に考えると、
確率的にみて尤もらしい値=最大値(最小値)=傾きがゼロ=微分した結果がゼロ
と言い換えることができます。
一般化したイメージをさらに普遍的に扱えるようにする
この一般化したイメージをさらに普遍的なものに落とし込みます。
先程の例は二項分布でしたがより一般的には、課題に対して最適なある分布に従う確率密度関数(あるいは確率質度関数)を設定することから始まります。これを一般的には尤度関数$L(θ)$として置きます。θはパラメータを指します。この時二項分布の場合は次の式を得ることができます。
L(p) = P(X=k) = \binom{10}{3} p^3 (1-p)^7
先程の例は10個の中から赤玉を3つ取り出した時の確率質度関数でした。この程度なら手計算でも導出が可能ですが、例えば3866個取り出したときに737個赤玉だったとき手計算はとても煩雑です。この計算を簡単なものにするため両辺に対数を取ります。こうする事で積の計算から和の計算になり簡素化ができます。これを対数尤度関数と呼びます。
\log L(p) = \log \left( \binom{10}{3} p^3 (1-p)^7 \right)
残るは先程示したようにこの確率質度関数の確率的に尤もらしい値を探すことになります。対数尤度関数を一階微分してその値がゼロ(最大化する条件)となるパラメータを導出します。
\frac{d}{dp} \log L(p) = \frac{d}{dp} \left[ \log \binom{10}{3} + 3 \log p + 7 \log (1-p) \right]
積から和に変わったので、計算しやすくなりました。あとはこのパラメータ$p$に対して解を求めていくと
\frac{d}{dp} \log L(p) = \frac{3}{p} - \frac{7}{1-p}
これがゼロとなるパラメータ$p$を求めると、
P=3/10
が得られます。この尤もらしい値の事を最尤推定量と呼びます。
統計検定準一級統計学実践ワークブックと照らし合わせ
ここまでのイメージから一般化まで辿っていくと漸くWBの理解が進むのではないかと想像します。WBにおける最尤法関連の記載を引用すると
確率分布$F_θ$の確率密度関数(離散変数の場合は確率質度関数)を$f(x;θ)$とした時、標本の独立同一性から同時確率密度関数は積$L(θ) = \prod^n_{i=1} f(x;θ)$となる。これを$θ$の関数として扱うとき尤度関数とよび、尤度関数値は単に尤度とよばれる
ここまでが尤度関数の定義の部分
尤度は得られた標本が確率分布$F_θ$によってどれだけ生成されやすいかの指標と解釈できる。よって想定しているパラメータ領域内において尤度を最大化するパラメータ値をパラメータの推定量として用いることができ、これを最尤推定量とよぶ。
どれだけ生成されやすいか=どれだけ赤玉のでる確率が3/10になりやすいかとおきかえることができます。
尤度の対数をとると計算がしやすくなることが多く$l(θ) = \log L(θ) = \sum^n_{i=1} \log f(x;θ)$は対数尤度と呼ばれる。もちろん最尤推定量は対数尤度の最大化によっても得られる。
最大化=微分してゼロになる値と置き換えることができます。
このように定義すると正規分布に従う分布のとき標本平均はサンプル数が大きくなると母平均に等しくなる。という考えを超越しどんな確率密度関数(確率質度関数)にも適用できる便利な理論になります。このサンプルから母集団のパラメータを推定するという思考そのものもベイズ推論的なアプローチもあり、思考の幅が広がります。
以上となります。点推定の性質とセットで理解しておくと非常に便利ですが今回はここまで。