前置き
この記事は、友人らと開催した自主ゼミのLT用に用意したプレゼンだったのですが、思ったより参加者が少なく悲しかったのでその内容を共有したいと思います。
内容はゲームにおける円の当たり判定です。あらゆるゲームにおいて必須レベルの処理になるため、プログラミングをしている方で全く知らないという方はあまりいないと思いますが実際に作成したプレゼンといっしょに説明していきます。今回の解説では主にシューティングゲームを用いて話しています。
また、この話題をあげるにあたってサンプルコードを作成しました。
- Visual Studio 2022
- Dxlib
これらを使っていますのでもしサンプルコードを動かしたい方がいましたら以下のページを参考にして環境構築をしてください。使用言語はC++ファイルですがC言語です。
円と円の当たり判定
前提条件
シューティングゲームを使って話していくのですが前提として、 自機の当たり判定は自機の中心に円があり、そこが当たり判定になります。そのため、頭や足を少しかすめても死にません。(そのほうが楽に処理できるんですね)
そんな中、敵は弾幕を自機に向けて打っていきます。


この様に、避けなければ自機に敵の弾幕があたってピチュってしまいます。1面道中でスペルカード抱えてピチュったらタイトルに戻りたくなってしまいますよね...
ではこのとき、どの様に当たり判定を処理しているのでしょうか。
2つの弾幕があるとき、次の3つの状況が考えられます。
- 離れているとき
- くっついているとき (接しているとき)
- 重なっているとき (貫通しているとき)
人間はパット見で下2つがあたっていると判断することができます。
ですがプログラム君は人間的な直感で判断することはできません。そのために条件分岐などであたっていることを感知しなければならないのです。
そしてもう一つ確認があります。一番下の状況は現実的にはありえないですよね。現実世界で実際に2つのボールを転がしても貫通しないので一番下の状況にはなりません。しかし、ゲームではフレームレート(1秒間に更新する画面の枚数)に対して、移動速度がめちゃくちゃ速いとこの様にめり込んでしまいます。これを「あたっている」という判定にしないとすり抜けてしまいバグのもととなります。
そのため下2つに関して見ていきましょう。
解説
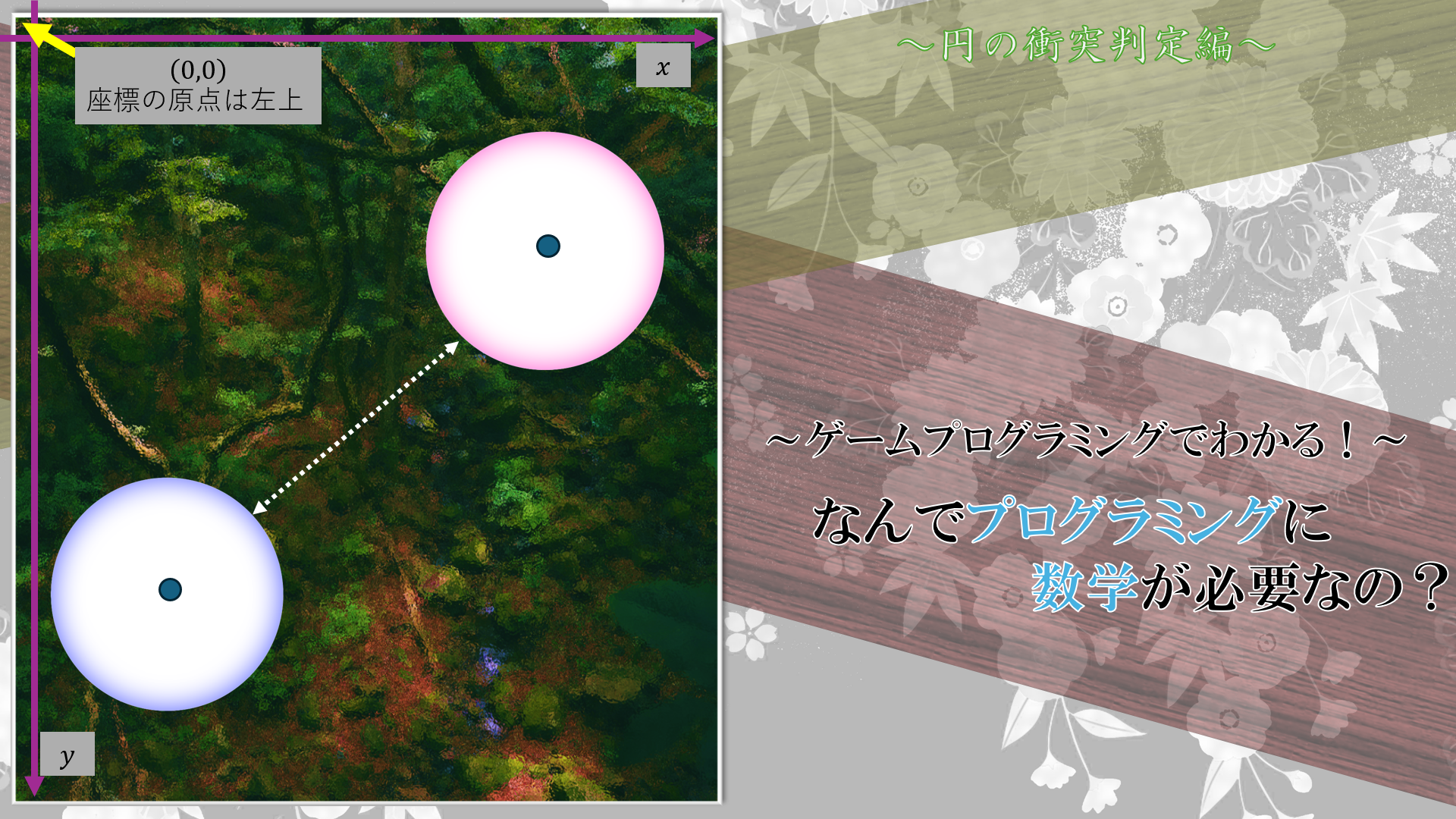
実際にゲームにおける情報を踏まえて見ていきます。ゲームの画面に何かを描画するときは座標を指定するのですが、数学における座標系と少し違って右上が原点となり、y座標が下に行くほど増えていきます。(これは処理系によるものだと思いますがこのようなものが多いと思います。)
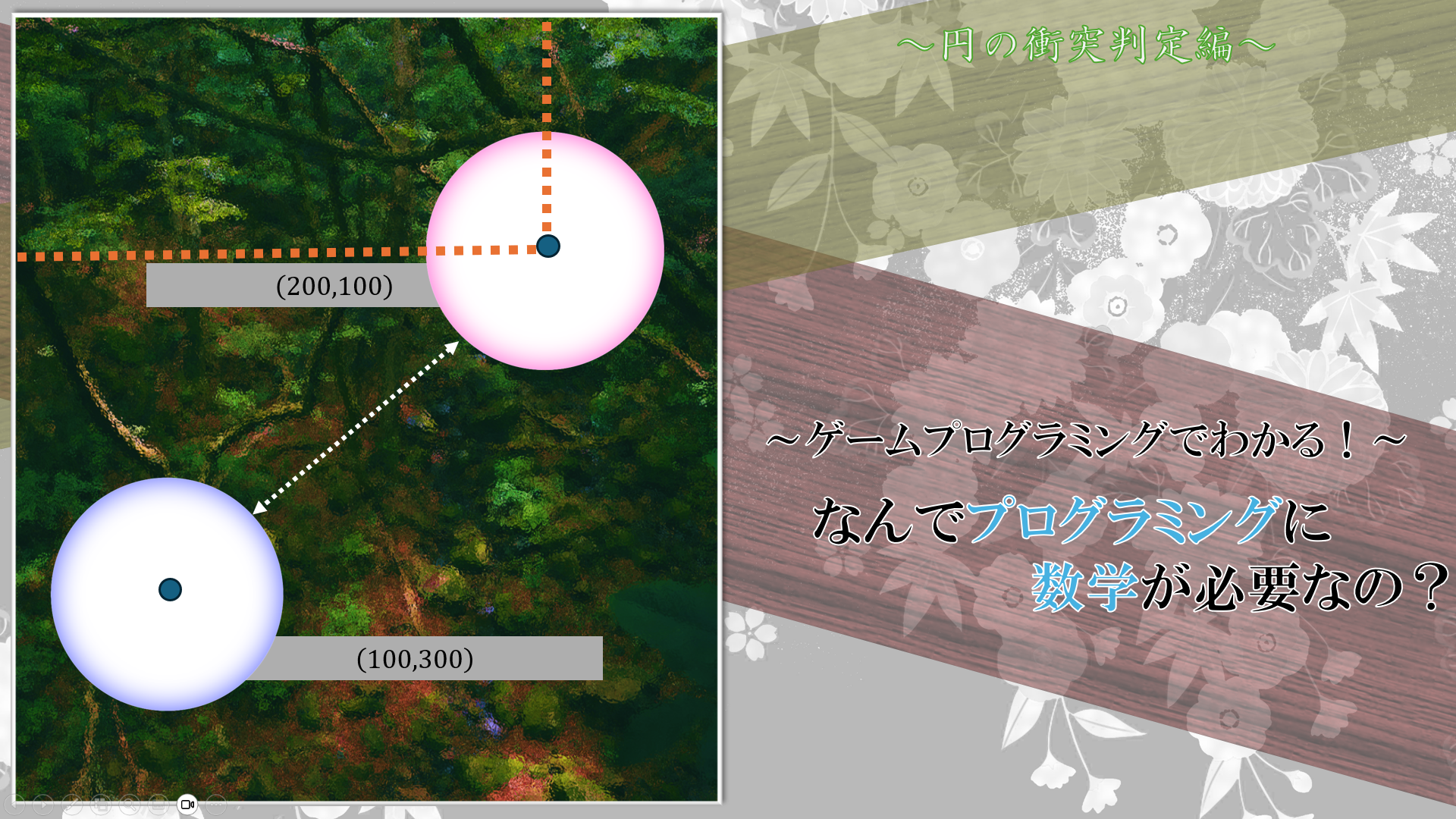
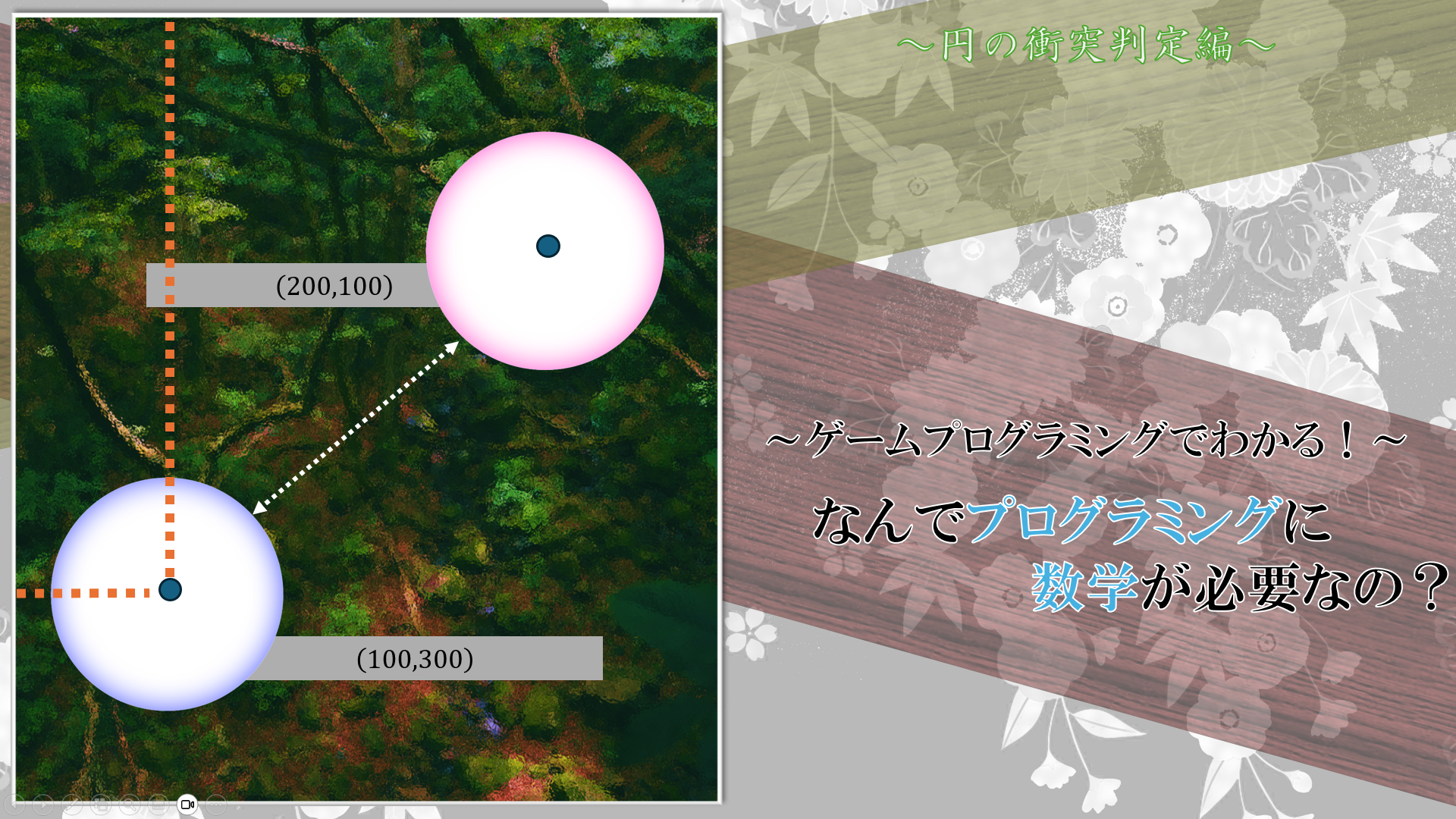
そして2つの弾幕はそれぞれの描画を行うために、中心座標及び半径がわかっているはずですね。数字はあくまでも参考程度に思ってください。これらの情報がわかっているときに2つの弾幕があたっているかいないかを判断するに何を見れば良いのでしょうか。
2つの弾があたっているときを具体的に見てみましょう。
図で示すとわかりやすいですね。お互いの中心座標までの距離がそれぞれの半径の和以下になればあたっているわけです。
2つの弾幕の距離を$d$とし、弾幕1の半径を$r_{1}$、弾幕2の半径を$r_{2}$とすれば
$$ d \leq (r_1 + r_2)$$
のとき、2つの弾幕があたっていると判定すればよいわけです。
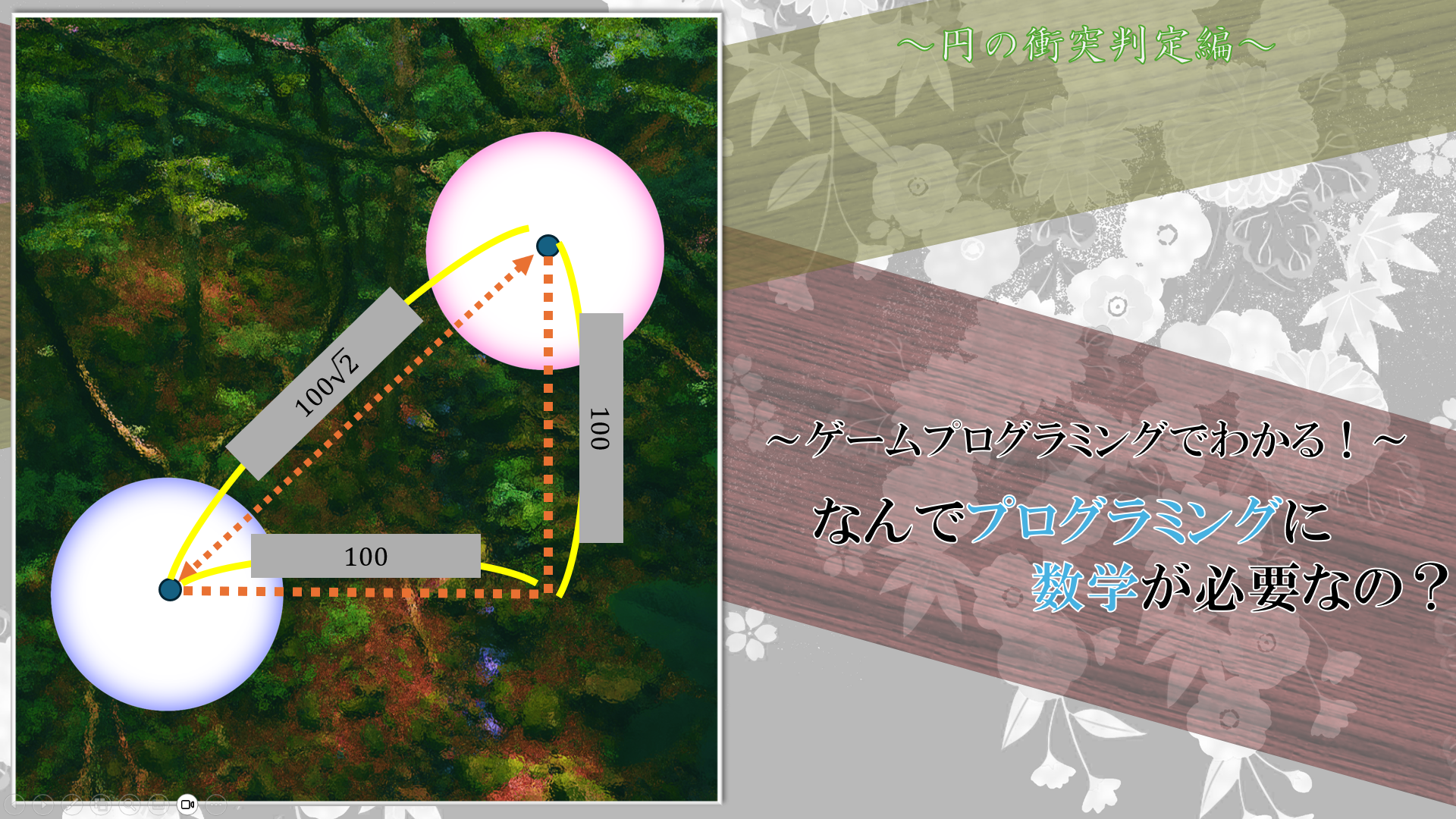
それでは、その$d$はどの様に求めればよいのでしょうか。これは中学数学で勉強した三平方の定理を用いればよいのです。
弾幕1の中心座標$(x_{1},y_{1})$、 弾幕2の中心座標$(x_{2},y_{2})$とするならば、弾幕の距離$d$は、
$$ d = \sqrt{((x_2 - x_1)^2 + (y_2 - y_1)^2)} $$
で求められます。
つまり、円同士の当たり判定は、
$$ \sqrt{((x_2 - x_1)^2 + (y_2 - y_1)^2)} \leq (r_1 + r_2)$$
を満たすときであるという条件分岐を作成すれば良いことがわかります。
サンプルコード
DxLibを用いたサンプルコードの内、円同士の当たり判定にまつわる部分のみ示します。(かなり拙いものですが)
コード全体は少し整理してからどこかに掲載します。
円同士の当たり判定:
#include "DxLib.h"
#include <stdio.h>
#include <math.h>
#define POWER(x) (x)*(x)
// 2次元のベクトルとして考える
typedef struct {
float x, y;
}Vector2D;
typedef struct {
Vector2D p; // 位置ベクトル
float r; // 半径
}Circle2D;
// DxLib使用時のmain関数(ウィンドウ画面生成時のmain関数)
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow) {
// DXライブラリ初期化処理
if (DxLib_Init() == -1)
{
return -1; // エラーが起きたら直ちに終了
}
// 円の生成
Circle2D c1 = { {100,100},100 };
Circle2D c2 = { {100,300},100 };
// 色情報の保存
int white = GetColor(255, 255, 255);
// 当たり判定のフラグ
int hit_flag = 0;
// キーが押されるまでループします
while (CheckHitKeyAll() == 0)
{
// メッセージループに代わる処理をする
if (ProcessMessage() == -1)
{
break; // エラーが起きたらループを抜ける
}
// 画面上の文字を消去
clsDx();
// 円を白色で描画する
DrawCircle(c1.p.x, c1.p.y, c1.r, white);
DrawCircle(c2.p.x, c2.p.y, c2.r, white);
// 距離の計算
float d = sqrt(POWER(c2.p.x - c1.p.x) + POWER(c2.p.y - c1.p.y));
// あたっているかの判定
if (d <= c1.r + c2.r) {
hit_flag = 1;
}
else {
hit_flag = 0;
}
// ウィンドウ画面における標準出力によって確認
if (hit_flag == 1) {
printfDx("HIT!!\n");
}
else {
printfDx("not HIT\n");
}
}
DxLib_End();
return 0;
}
このコードで円の中心座標や半径を変更して正常に当たり判定を出力してくれるのかを確認してみてください。
最後に
プログラムに関しては、あまりきれいなコードでは無いかもしれないのでそこは目を瞑っていただけると幸いです。
また、このプレゼンは続きがあって、円とカプセル型の当たり判定もまとめています。今後それについても記事にまとめて投稿するかもしれません。