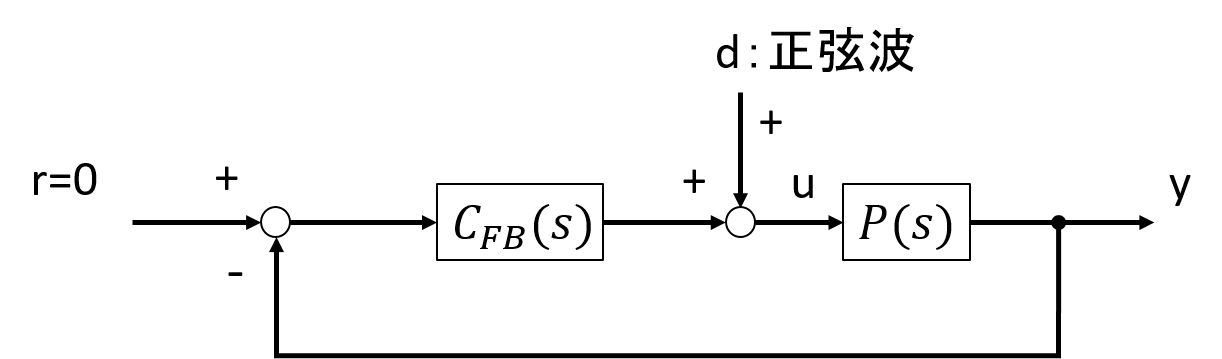はじめに
メカトロ系のモデルベース制御を行う上で大事なのが、制御対象のモデルを獲得すること。ひいては、そのモデルを作るために、元となる特性を把握する必要があります。
特性を把握する方法としてM系列信号(『周波数領域におけるシステム同定の性能評価 』,足立,室井,2008)やステップ信号などがありますが、その他に有効な方法として、正弦波掃引法があります。
正弦波掃引法とは、制御対象P(s)へ外部信号dとして正弦波を加え、その時の入出力u,yを高速フーリエ変換(FFT)により解析することで、周波数特性を得る方法です。このとき、入力指令rは0とします。
このとき、制御対象が不安定系の場合だと出力が発散してしまうため、フィードバック制御器C_FB(s)を加えて対処することがあります。
ブロック線図で示すとこんな感じです。
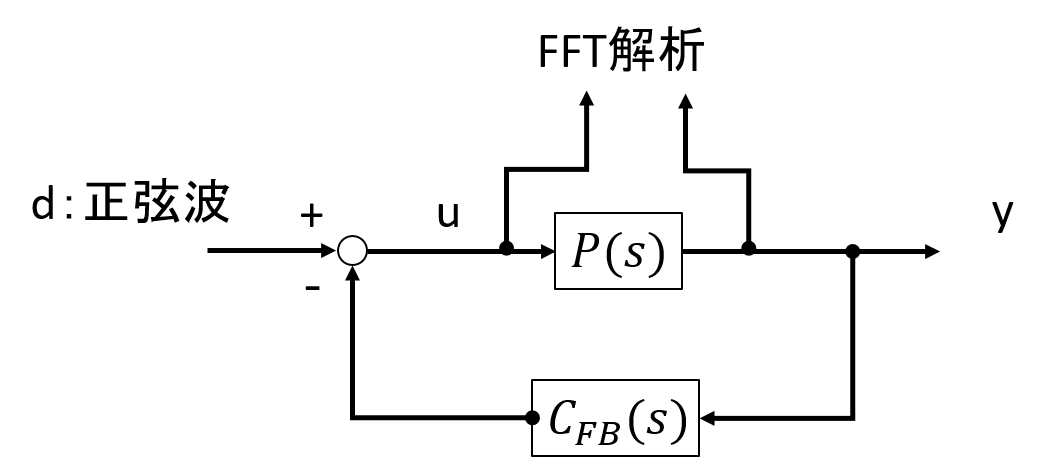
正弦波は外部信号(外乱)dとして加えるわけですが、入力指令rがないので、次の図のように置き換えることができます。
以下、pythonを用いた正弦波掃引法のプログラムについて説明します。
制御対象の設定
完全なるシミュレーションなので、制御対象もこちらで設定します。
プログラムは以下のとおりです。
from control.matlab import *
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy import signal
# ボード線図(制御対象の特性)
# 制御対象のパラメータ(2慣性、剛体モード+2次までの振動モードとする)
kt=10
# 剛体モード
k0=100
# 1次振動モード
k1=100
zeta1=0.2
omega1=30*2*math.pi
# 2次振動モード
k2=100
zeta2=0.04
omega2=200*2*math.pi
# むだ時間L(4次のパデ近似で表現)
L=500e-6
deadtime_num,deadtime_den=pade(L,4)
deadtime_sys=tf(deadtime_num,deadtime_den)
# 制御対象の伝達関数
P=kt*(tf(k0,[1,0,0])+tf(k1,[1,2*zeta1*omega1,omega1**2])+tf(k2,[1,2*zeta2*omega2,omega2**2]))*deadtime_sys
# ボード線図の表示範囲
fmin=1
fmax=1000
wrange=linspace(fmin*2*math.pi,fmax*2*math.pi,400)#角周波数で指定
# ボード線図
bode(P,wrange)
制御対象の伝達関数は次式となります。
P(s)=k_t\Biggl(\frac{k_0}{s^2}+\frac{k_1}{s^2+2\zeta_1\omega_1+\omega_1^2}+\frac{k_2}{s^2+2\zeta_2\omega_2+\omega_2^2}\Biggr)e^{-Ls}
pythonにおける伝達関数は、control.matlabライブラリにあるtf関数で作成することができます。また、むだ時間のパデ近似はcontrol.matlabライブラリにあるPade関数で作成できます。
制御対象の数学モデルを表す際、運動方程式を用いた物理モデルを用いることが多いのですが、剛体モード・振動モードを用いた表現のほうが個人的に馴染み深いので、こちらを用います。一部の論文でも使われている表現です。
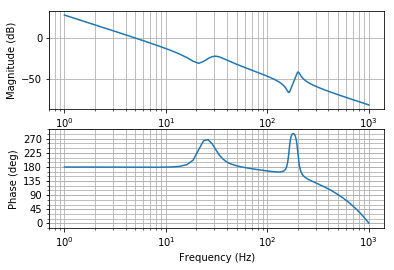
ボード線図は以下のようになります。
図より、30Hz、200Hz付近でそれぞれ共振・反共振が出ているのがわかります。加えて、むだ時間により100Hz以降で位相遅れが発生しています。
正弦波掃引法により、このボード線図と同じ特性を得ることが、今回の目的になります。
正弦波掃引時の応答
まず、制御対象に正弦波を掃引したときの応答について説明します。プログラムは以下の通りです。
# 正弦波入力時の応答(周波数応答)
from control.matlab import *
import numpy as np
import matplotlib.pyplot as plt
# 制御対象が不安定系なので、フィードバック制御器(PID)を用いる
kp=3
kd=0.5
ki=10
C_FB=tf([kd,kp,ki],[1,0])
G_du=1/(1+P*C_FB)#入力
G_dy=P/(1+P*C_FB)#出力
Td=np.arange(0,2,0.01)#時間の取得
# 複数の周波数について図を見せるための措置
freq=[1,20,30,60]
count=0
fig,ax=plt.subplots(2,2)
for i in range(2):
for j in range(2):
d=np.sin(freq[count]*Td)
#正弦波を入力したときの応答
y,t,X0=lsim(G_dy,d,Td,0)
u,t,X0=lsim(G_du,d,Td,0)
ax[i,j].plot(t,u,ls='--',label='u')
ax[i,j].plot(t,y,label='y')
count+=1
ax[0,0].legend()
plt.show()
プログラム前半はPID制御(フィードバック制御)器の設計、定常応答(発散しない状態)になればいいので、設計は割とゆるめで構いません。
正弦波を入力したときの応答を調べるためには、外部信号から入出力までの伝達関数が必要なのですが、先程のブロック線図から、伝達関数は次のように表されます。
\frac{u(s)}{d(s)}=\frac{1}{1+P(s)C_{FB}(s)} \\
\frac{y(s)}{d(s)}=\frac{P}{1+P(s)C_{FB}(s)}
時間応答については、control.matlabライブラリにあるlsim関数でシミュレーションできます。
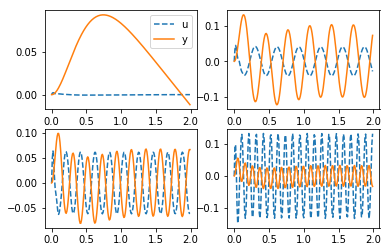
構築した制御系に正弦波を加えると、以下のような時間応答が得られます(横軸が時間、縦軸が応答の大きさ、各グラフで縦軸のメモリが異なるので注意)。
青破線が入力u,オレンジの実線が出力yになります。
左上から、周波数1Hz、20Hz、30Hz、60Hzの外部信号を加えたときの応答です。入力uに対して出力yが大きいほど周波数特性のゲインが大きく、小さいほどゲインは小さくなります(等倍で0dB)。一方、時間軸でのずれは位相のずれになります。
このとき、最初の数周期は出力が安定していないのがわかります。こうした定常でない部分は解析の妨げになるので、解析前に切り取ることもあります。
応答波形の解析
最後に、獲得した応答の解析です。プログラムを以下に示します。
from control.matlab import *
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy import signal
freq=np.linspace(1, 1000, num=400)#周波数
Ts=500e-6#サンプリング周期
gain_li=[]#ゲイン、プロット用
phase_li=[]#位相、プロット用
fig2,ax2=plt.subplots(2,1)
# 周波数の数だけfor文
for f in freq:
#正弦波の周期*500だけの時間を作る
Td=np.arange(0,1/f*500,Ts)
#正弦波を作る
d=np.sin(2*math.pi*f*Td)
#入出力の応答測定
y,t,X0=lsim(G_dy,d,Td,0)
u,t,X0=lsim(G_du,d,Td,0)
#両方をFFT変換しゲイン・位相を取る
# 窓関数
y_start=int(len(y)/2)
y_end=len(y)
wf = signal.hann(y_end-y_start)# ハニング窓
#FFT
y_fft=rfft(y[y_start:y_end]*wf)
u_fft=rfft(u[y_start:y_end]*wf)
#y
gain_y = max(np.abs(y_fft)) #ゲイン
max_index_y=np.argmax(y_fft) #ゲインを取るときのデータインデックス
im_y=y_fft[max_index_y].imag #虚部
re_y=y_fft[max_index_y].real #実部
phase_y=math.atan2(im_y,re_y) #位相
#u
gain_u = max(np.abs(u_fft))
max_index_u=np.argmax(u_fft)
im_u=u_fft[max_index_u].imag
re_u=u_fft[max_index_u].real
phase_u=math.atan2(im_u,re_u)
#ゲイン差・位相差を取る
gain=20*np.log10(gain_y/gain_u)
phase=(phase_y-phase_u)*180/math.pi
#取った差をリストに入れる
gain_li.append(gain)
phase_li.append(phase)
ax2[0].semilogx(freq,gain_li)#周波数-ゲイン
ax2[1].semilogx(freq,phase_li)#周波数-位相
plt.show()
流れを説明すると、
・正弦波の生成
・窓関数による事前処理
・RFFTによる正の周波数のみの複素数表示
・絶対値によるゲイン獲得
・逆正接関数による位相獲得
となります。
正弦波の生成については、定常な波形を得るために100周期以上の波形が流れるようになっています。高周波では定常波形になるまで何周期分もの時間がかかります。生成する時間を長めに設計するとしないとでは、得られる測定結果は大きく変わります。
窓関数についてはググってもらえると色々あるのですが、簡単に言えば周波数成分を変えないようにしつつ応答の始めと終わりを0にする関数です。これをしないとFFTの精度が落ちてしまいます。
FFT(高速フーリエ変換)についても詳細はググってほしいのですが、pythonではfftライブラリを使えば簡単に複素数表示にしてくれます。
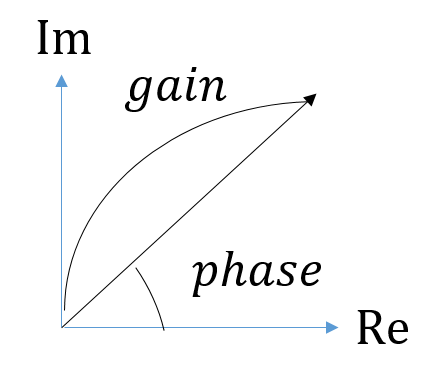
ゲインと位相については、図で考えるとこんな感じです。矢印の長さ(絶対値)がゲイン、角度が位相というわけです。
すなわち、複素数表示で表されたFFT解析結果を、以下のように計算することでゲイン・位相が得られます。
gain=20log\bigl(\sqrt{{Re}^2+{Im}^2}\bigr)\\
phase=tan^{-1}\biggl(\frac{Im}{Re}\biggr)
ゲインについてプログラム上では絶対値absを使って計算しています。
FFT解析結果は各周波数について出てくるのですが、外部信号は1つの周波数成分しか持たないので、解析結果の中で最も強い(複素数が大きい)周波数成分と外部信号の周波数成分はおなじになるはず。なので、max関数で出した部分をゲイン・位相のためのデータとして採用しています。
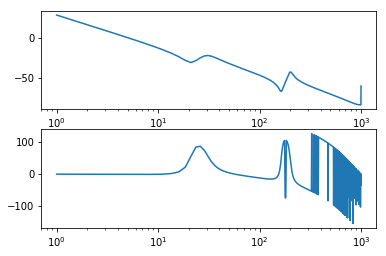
そんなわけで、得られた周波数特性が以下の図になります。
なぜか位相が0度中心になっているのが気にかかりますが、共振部分のゲイン・位相がバッチリ取れているのがわかります。
周波数毎のデータを取らなければならない分時間がかかるのが難点ですが、精度はピカイチの正弦波掃引法。
システム同定の際は是非試してみてください。