ビットを反転させる操作の仕組み
コンピュータが引き算をするためには、引く数を2の補数表現にして、「2の補数を足す」必要があります。
また、2進数を2の補数表現にするためには、各ビットの値を反転させ、「$1$」を加えるという操作が必要になります。
これらの操作において、足し算に関しては半加算器と全加算器を使うことで実行することができるのですが、「ビットを反転させる」という操作については特殊な操作が必要になります。
ビットを反転させる操作を可能にするためには**排他的論理和(EOR)**と「反転させたい場所と同じ位置に『$1$』がくるビット列」を使用します。
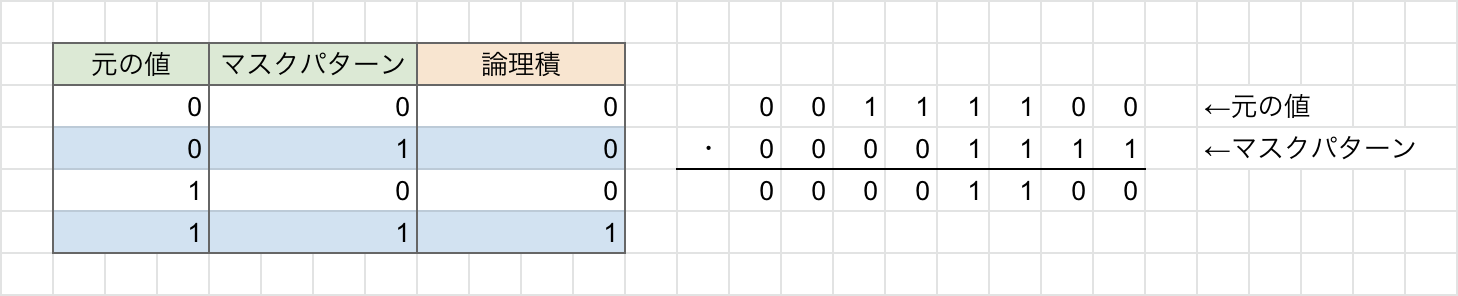
この理由を理解するために排他的論理和(EOR)の真理値表を以下に示します。

まず、排他的論理和(EOR)についてですが、この論理演算の特徴として、「演算する値が同じ場合には『$0$』を返し、異なる場合には『$1$』返す」というものがあります。
この特徴を踏まえて青色の行に注目してみます。この行では「元の値」がそれぞれ「$0$」と「$1$」になっています。その一方で、「加えた値」についてはどちらも「$1$」になっています。
この表から、元の値が「$0$」のとき、同じ位置に「$1$」を置いて、排他的論理和の論理演算を行うと「$1$」に反転し、元の値が「$1$」の時も同様の操作を行うことで値が反転するということが分かります。
次に、この操作を具体例を用いて確認してみたいと思います。
たとえば、「$00111100$」という8ビットの数のうち、右から4ビット目までの値「$1100$」を反転させたいとします。
そのために、まずは右から4ビット目までが「$1$」である8ビットの数「$00001111$」を用意します。そして、これらのビット列を排他的論理和(EOR)で論理演算します。
演算の様子を以下の図に示します。
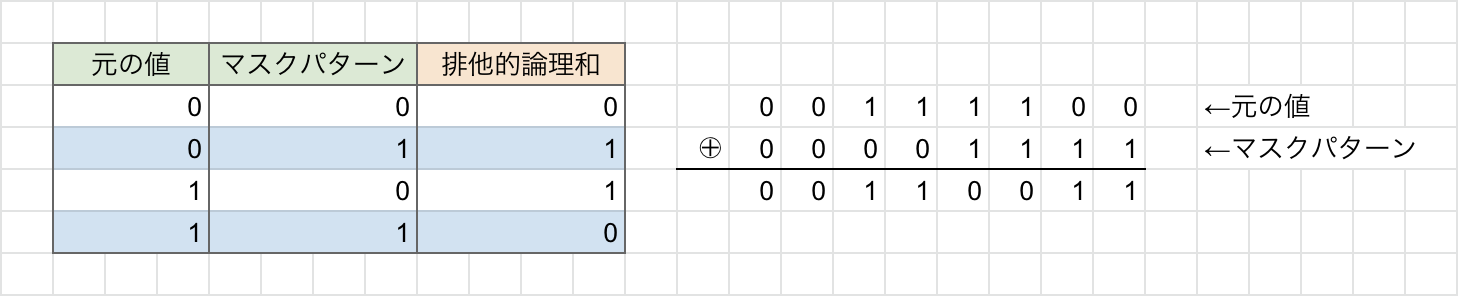
この図から、元の数の右から4ビット目までの値が排他的論理和(EOR)によって反転されていることが分かります。
このために用意した、「$00001111$」という右から4ビット目までが「$1$」の数のことをマスクパターンと呼びます。
したがって、ビット列を反転させる時には、反転させたいビット列と同じビットに「$1$」を入れたマスクパターンを用意し、排他的論理和(EOR)で論理演算すれば良いということになります。
ビットを抽出する操作の仕組み
コンピュータが特定のビット列を抽出するときの操作についてですが、この場合も先ほどの反転操作と同様に、抽出したいビット列と同じビットに「$1$」を入れたマスクパターンを使用します。
また、抽出するための操作として、論理積(AND)を使います。
元の値とマスクパターンを論理積(AND)の真理値表で表現すると以下の図のようになります。
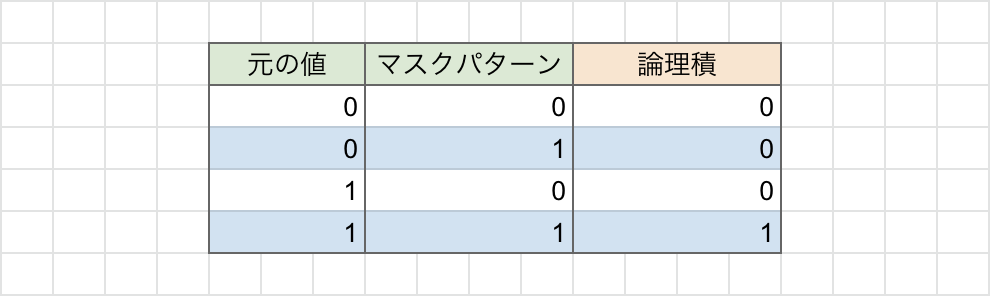
まず、論理積(AND)についてですが、この論理演算の特徴として、「演算する値が両方とも『$1$』の場合には『$1$』を返し、それ以外の場合には『$0$』を返す」というものがあります。
この特徴を踏まえて青色の行に注目してみます。青色の行では「元の値」がそれぞれ「$0$」と「$1$」になっています。一方で、「マスクパターン」についてはどちらも「$1$」になっています。
この表を踏まえると、元の値が「$1$」のとき、マスクパターンの同じ位置に「$1$」を置いて、論理積の論理演算を行うと「$1$」になることが分かります。
また、元の値が「$0$」のとき、マスクパターンの同じ位置に「$1$」を置いて同様の操作を行うと「$0$」になることが分かります。
次に、この操作を具体例を用いて確認してみたいと思います。
たとえば、「$00111100$」という8ビットの数のうち、右から4ビット目までの値「$1100$」を抽出したいとします。
そのために、まずは右から4ビット目までが「$1$」である8ビットの数「$00001111$」を用意します。そして、これらのビット列を論理積(AND)で論理演算します。
この図から、元の数の右から4ビット目までの値が排他的論理和(EOR)によって反転されていることが分かります。
したがって、ビット列を抽出する時には、抽出したいビット列の部分(ビット)に「$1$」を入れたマスクパターンを用意し、論理積(AND)で論理演算すれば良いということになります。
参考にさせて頂いた書籍
きたみりゅうじ 『キタミ式イラストIT塾 基本情報技術者平成31/01年』 技術評論社 2019年
学習してみて
以前から引き算について学習してから、2進数の引き算をする時に、コンピュータはどうやって2の補数を作ってるんだろうかと気になっていたのですが、今回の学習でその仕組みをようやく知ることが出来ました。
結構複雑なのかと身構えていたのですが、案外そうでもなかったのでかえって驚きました。
抽出の操作についても、論理演算を使えばこんなことも出来るのかと感心してしましました。
「n進数」の仕組みから始まり、コンピュータで四則演算やビット操作が出来るようになる仕組みまでを学習してきたわけですが、なかなか長かったですね。