32ビットの浮動小数点数
浮動小数点数を32ビットで表現したシンプルな形式になります。
配置は、左から1ビットを符号、その次から7ビットを指数部、そして残り24ビットを仮数部としています。
符号が正の場合には「$0$」、負の場合には「$1$」を入れます。
指数部が負の数の場合は2の補数で表現します。
仮数部には、仮数を1未満の小数で表した桁のうち、小数点以下の桁を格納します。

10進数を32ビットの浮動小数点数にする
実際に10進数の数を浮動小数点数にしてみたいと思います。
例として、「$9.875$」という10進数を浮動小数点数にしてみます。
手順① 10進数を2進数に基数変換する
まず、「$9.875$」を2進数に基数変換します。
整数部分の「$9$」は2進数で「$1001$」、小数部分の「$0.58$」は2進数で「$0.111$」となります。
この2つをくっつけて、10進数「$9.875$」は2進数で「$1001.111$」となります。
手順② 2進数を指数表記にする(正規化)
次に、2進数「$1001.111$」を指数表記にします。
指数表記では、仮数が1未満の小数になる形にします。つまり、「$0.M$」という形に正規化します。
この通りにすると、仮数は「$1001.111$」の小数点を左に4桁動かした「$0.1001111$」という形になります。仮数がこの形になったので、指数を調整すると、「$0.1001111\times2^4$」になります。
手順③ 浮動小数点数のビットに格納する
今度は、指数表記から浮動小数点数に格納する数を抜き出します。
仮数の符号は正なので、浮動小数点数の符号部分に入る数は「$0$」になります。
指数は「$4$」なので、浮動小数点数の7ビットの指数部に入る2進数の形にすると「$0000100$」になります。
仮数部は先ほど求めた仮数「$0.1001111$」の小数点以下の数、「$1001111$」を格納します。
仮数部は24ビットあるので余ってしまいますが、「$0.1001111$」を「$0.1001111000...$」という形で$0$で埋めて表現しても同じ値になります。だから、仮数部には「$1001111$」を入れて残りのビット全てを「$0$」で埋めます。
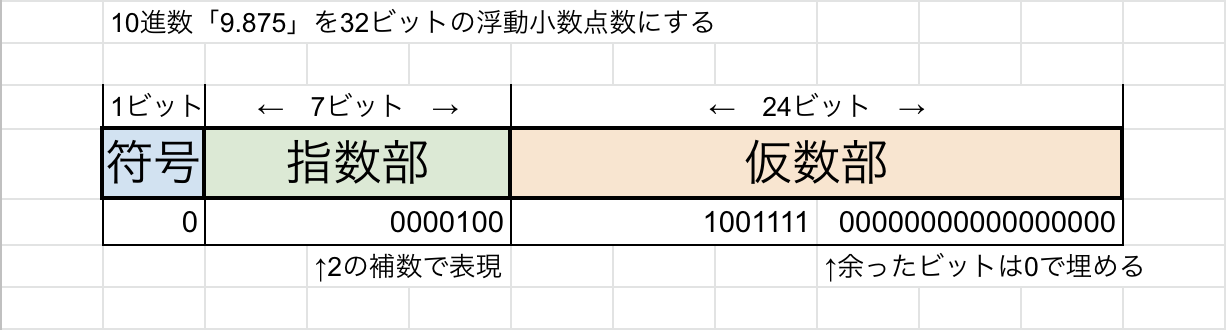
すると、10進数「$9.875$」を32ビットの浮動小数点数にした値は
「$00000100100111100000000000000000$」
となりました。
IEEE754形式の浮動小数点数
IEEE(米国電子電気技術者協会)によって規格化された形式になります。
32ビット形式の他に64ビット、128ビット形式がありますが、今回は32ビット形式について取り上げます。
配置は、左から1ビットを符号、その次から8ビットを指数部、そして残り23ビットを仮数部としています。
符号が正の場合には「$0$」、負の場合には「$1$」を入れます。
ここまでは先ほどの32ビット形式の浮動小数点数とそれほど大きな違いはありません。
しかし、指数部と仮数部の扱いに関してはかなり異なっています。
指数部について、まず指数を8ビットの2進数に基数変換した数を用意します。このとき、2進数は2の補数表現にします。さらにその数に「$01111111$(10進数で127)」を足した数を入れます。
このように、2の補数に「$01111111$(10進数で127)」を足すことをバイアス127と呼びます。
仮数部には、仮数を2進数10未満の小数を含む数で表した桁のうち、小数点以下の桁を格納します。つまり、「$1.M$」の形に正規化した上で、$M$の部分を格納します。

10進数をIEEE754形式の浮動小数点数にする
実際に10進数の数をIEEE754形式の浮動小数点数にしてみたいと思います。
例として、「$9.875$」という10進数を浮動小数点数にしてみます。
手順① 10進数を2進数に基数変換する
まず、「$9.875$」を2進数に基数変換します。
整数部分の「$9$」は2進数で「$1001$」、小数部分の「0.58」は2進数で「$0.111$」となります。
この2つをくっつけて、10進数「$9.875$」は2進数で「$1001.111$」となります。
手順② 2進数を指数表記にする(正規化)
次に、2進数「$1001.111$」を指数表記にします。
指数表記では、仮数が10未満の小数を含む数にします。つまり、「$1.M$」という形に正規化します。
この通りにすると、仮数は「$1001.111$」の小数点を左に3桁動かした「$1.001111$」という形になります。仮数がこの形になったので、指数を調整すると、「$1.001111\times2^3$」になります。
手順③ 浮動小数点数のビットに格納する
今度は、指数表記から浮動小数点数に格納する数を抜き出します。
仮数の符号は正なので、浮動小数点数の符号部分に入る数は「$0$」になります。
指数は「$3$」なので、8ビットの2進数にすると、「$00000011$」となります。
さらに、この数に「$01111111$」を加えると、「$10000010$」となります。この数を指数部に格納します。
仮数部は先ほど求めた仮数「$1.001111$」の小数点以下の数、「$001111$」を格納します。
仮数部は23ビットあるので余ってしまいますが、「$1.001111$」を「$1.001111000...$」という形で$0$で埋めて表現しても同じ値になります。だから、仮数部には「$001111$」を入れて残りのビット全てを「$0$」で埋めます。

すると、10進数「$9.875$」をIEEE754形式の32ビットの浮動小数点数にした値は
「$01000001000111100000000000000000$」
になりました。
IEEE754形式のメリット
IEEE754形式のメリットは2つあります。
1つ目は、正規化で仮数を「$1.M$」という形式にすることにより、有効な桁を確保しつつ1ビット多く表現できることです。
2つ目は、指数を2の補数の数として表現し、「$01111111$」を足すこと(バイアス127)によって符号ビットが無くなり、指数部の大小関係が分かりやすくなることです。
正規化によるメリット
まず、1つ目のメリットについて取り上げます。
たとえば「$0.0011$」のように小数点以下に「$0$」が入る2進数をそれぞれの形式に合わせて正規化した時のことを考えてみます。
シンプルな32ビット形式では「0.M」の形式で正規化するため「$0.11\times2^{-2}$」となります。
一方で、IEEE754形式では「1.M」の形式で正規化するため「$1.1\times2^{-3}$」となります。
| 形式 | 元の数 | 指数表現 | 仮数 | 仮数部に入る数($M$) | |
|---|---|---|---|---|---|
| シンプルな32ビット形式 | $0.0011$ | $0.11\times2^{-2}$ | $0.11$ | $11$ | |
| IEEE754形式 | $0.0011$ | $1.1\times2^{-3}$ | $1.1$ | $1$ |
両者を比較すると、同じ数を表現して有効な桁を収めているにも関わらず、仮数の桁数が違っていることがわかります。
つまり、シンプルな32ビット形式では2桁の数「$11$」を仮数部に入れますが、IEEE754形式では1桁の数「$1$」だけで済むわけです。
したがって、IEEE754形式では、正規化で仮数を「$1.M$」という形式にすることにより、有効な桁を確保しつつ浮動小数点数で1ビット多く表現することができます。
バイアスによるメリット
次に、2つ目のメリットについて取り上げます。
指数表現で「$11.1$」と「$0.00111$」の2つの2進数を浮動小数点数にする場合について考えたいと思います。
まず、シンプルな32ビット形式で2つの数を指数表記すると、次のようになります。
| 元の数 | 指数表現 | 指数 (10進数) | 指数部(7ビット) | |
|---|---|---|---|---|
| $11.1$ | $0.111\times2^{3}$ | $3$ | $0000011$ | |
| $0.00111$ | $0.111\times2^{-2}$ | $-2$ | $1111110$ |
次に、IEEE754形式で2つの数を指数表記すると、次のようになります。
| 元の数 | 指数表現 | 指数 (10進数) | 指数部(8ビット) | |
|---|---|---|---|---|
| $11.1$ | $1.11\times2^{1}$ | $1$ | $10000000$ | |
| $0.00111$ | $1.11\times2^{-3}$ | $-3$ | $01111100$ |
ここで、この2つの形式のうち、指数部の表現に着目します。
どちらの形式においても一度2の補数表示にしてから指数を表現しています。
シンプルな32ビット形式では、指数を2の補数にしたものをそのまま指数部に格納します。
そのため、正の数と負の数が指数部に格納されていることになります。
IEEE754形式では指数を8ビットの2の補数表示にするところまでは同じです。
元の数が「$11.1$」ならば指数は「$00000001$」(10進数で「$1$」)になります。
また、元の数が「$0.00111$」ならば指数は「$11111101$」(10進数で「$-3$」)になります。
ここで、この指数の状態をよく見ると、「8ビットのうち左から1ビットを符号ビット、残り7ビットを整数とした固定小数点数」と同じ形になっていることがわかります。
下の表はこの固定小数点数の各桁の構造と最大値・最小値をまとめたものです。
| 桁数 | 符号ビット | 7 | 6 | 5 | 4 | 3 | 2 | 1 |.| 10進数 |
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
| | | | | | | | | | | |
|(最小値)| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | -128 |
| | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | | -127 |
| | … | … | … | … | … | … | … | … | | … |
| | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | 0 |
| | … | … | … | … | … | … | … | … | | … |
| | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |126|
|(最大値)| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |127|
この表から、固定小数点数、つまり「指数を8ビットの2の補数として表現した数」が表すことができる範囲は「$-128$〜$127$」であることが分かります。
| 8ビットの固定小数点数における整数 (符号あり) | |
|---|---|
| 最小値 | $-128$ ( $-2^{(8-1)}$ ) |
| 最大値 | $127$ ( $2^{(8-1)}-1$ ) |
| 範囲 | $-128$ 〜 $127$ |
IEEE754形式はこの範囲で表現された指数に「$01111111$」(10進数で「$127$」)を加えます。
すると、10進数で「$-127$」を表す2進数の2の補数「$10000001$」に「$01111111$」が足されて「$100000000$」になります。
2の補数の性質から、桁上がりした9ビット目の「$1$」を無視すると「$00000000$」、つまり10進数で「$0$」になります。
また、「$-128$」を表す2進数の2の補数「$10000000$」に「$01111111$」が足されて「$11111111$」になります。
この数は10進数で「$255$」になります。
これにより、指数を表現できる範囲が「$0$〜$255$」へ変化しました。ただし、これは指数の元の数とは異なった数であることに注意が必要です。
したがって、「指数を8ビットの2の補数として表現した数」の時点では、「シンプルな32ビット形式」のように指数部に正の数と負の数が格納されていたわけですが、「$01111111$」(10進数で「$127$」)を加えたことにより、正の数だけを扱うようになりました。
このことを踏まえて、改めてシンプルな32ビット形式とIEEE754形式を見比べてみます。
【シンプルな32ビット形式】
| 元の数 | 指数表現 | 指数 (10進数) | 指数部(7ビット) | |
|---|---|---|---|---|
| $11.1$ | $0.111\times2^{3}$ | $3$ | $0000011$ | |
| $0.00111$ | $0.111\times2^{-2}$ | $-2$ | $1111110$ |
【IEEE754形式】
| 元の数 | 指数表現 | 指数 (10進数) | 指数部(8ビット) | |
|---|---|---|---|---|
| $11.1$ | $1.11\times2^{1}$ | $1$ | $10000000$ | |
| $0.00111$ | $1.11\times2^{-3}$ | $-3$ | $01111100$ |
シンプルな32ビット形式では指数が2の補数表示のままであるため、「$11.1$」と「$0.00111$」の指数の大小関係を比べる時に直感的に分かりづらいです。
しかし、IEEE754形式では指数部がすべて正の数であるため、「$11.1$」と「$0.00111$」の指数の大小関係を比べる時に直感的に分かりやすいです。また、指数部をそのまま引き算することで指数の差を求める事もできます。
したがって、IEEE754形式には、指数を2の補数の数として表現し、「$01111111$」を足すこと(バイアス127)によって符号ビットが無くなり、大小関係が分かりやすくなります。
参考にさせて頂いた書籍
きたみりゅうじ 『キタミ式イラストIT塾 基本情報技術者平成31/01年』 技術評論社 2019年
学習してみて
固定小数点指数、浮動小数点数とこれまでより一段と複雑になってきたなと感じています。
特にIEEE754形式を採用するメリットの理解はなかなか難しかったです。
ただ、実際に色んな数をシンプルな32ビット形式にして、同じ数をIEEE754形式にするプロセスと比べてみて「なるほど!」と理解できました。
理解できた時、IEEE754形式が非常に無駄のないものとして設計されていることに驚きました。
コンピューターにはきっとこの他にも天才達が合理的に設計した仕組みが散りばめられているのでしょうね。
知れば知るほど奥深いです。