イベント人員分配を制約充足問題として解いてみよう

背景

仕事で最適化問題を取り扱う事があり、離散最適化を応用してみたことがありました。
最初はイメージつかなかったのですが、応用範囲が広いことに気づき、だんだん楽しくなってきました。
主に、Google OrToolsというライブラリを使っています。
https://developers.google.com/optimization

実は、会社のアドベントカレンダーで投稿した記事の再投稿です。

例題

例題は、仕事とは全く関係なく、妻にから依頼された相談をちょっと脚色して問題にしています。

• イベントを5日間開催します。
• 1人1回だけイベントに参加できます
• 5日間のうち、最初の2日間は大会場、残り3日間は小会場で収容人数が異なります。
  　収容人数を超える人は受け入れできません。
  • 大会場 35人
  • 小会場 10人
• 参加可能日を聞くためにアンケートを取ります
  • 5日間のうち、参加可能な日を優先順に記入
  • できるだけ多くの人を優先順位が高い日に割り振って欲しい

このように、数学的に制約を表現でき、制約を満たす解を探す問題を
離散最適化では制約充足問題というようです。

妻から依頼された時はGoogle ORToolsを使わずにExcelで答えを出しました。
そのときのアルゴリズムは、制約がきつい人（希望日が少ない人）順に優先的に割当てていく方式を取りました。
シンプルなアルゴリズムですが、それでも十分良い結果になっていました。

勉強したこと

いくつか基礎知識はある状態で、下記eラーニングを一通りやってみました。
https://jp.coursera.org/learn/discrete-optimization#instructors
英語でハードルは若干高いですが、テストも充実していて勉強になりました。

Google OrToolsの使い方は、公式ドキュメントがわかりやすいと思います。
https://developers.google.com/optimization/introduction/python

実装

Google OrToolsのインストール

今回はGoogle Colaboratory上で検証しました。
ライブラリはpipで一発でインストールできます。

!pip install ortools
from ortools.sat.python import cp_model
import random

サンプルデータの生成

参加希望日を表すリストをランダム作成します。
例：[4，1] となっていれば、5日目が第一希望で、2日目が第二希望という意味です。

random.seed(1)
event_day_num = 5   # イベントの日数
attendance_list = [] # 参加可能な日
capacity = [30,30,15,15,15]
n = 100 # 参加人数
for attend_day_num in random.choices(range(1,event_day_num+1),weights=[0.6,0.2,0.1,0.05,0.05],k=n):
  attendance_list.append(random.sample(range(event_day_num),k=attend_day_num))
attendance_list

生成したサンプルデータ

[[0],
 [3, 2, 4],
 [4, 1],
 [4],
 [3],
 [3],
 [2, 3],....

イベントに出席する日の変数を作成

人毎、日毎に出席の有無を表す変数を作ります。
この変数は、ただのPythonの変数ではなくて
最適化モデル上で値を探索したい変数です。
変数の取りうる範囲は２値（出席するなら１、しないなら０）とします。

model = cp_model.CpModel()
# イベントに出席する日の変数を作成
date_of_attendance = [
    [ 
        model.NewBoolVar(f"day{d}_man{m}")
        for d in range(event_day_num)
    ] 
    for m in range(n)
  ]

制約1：1人1回だけイベントに参加できる

作成した変数に制約を課していきます。
各人の変数の合計が1という制約を付けることで、必ず1回参加する制約を付与することができます。

for i in range(n):
  model.Add(sum(date_of_attendance[i]) == 1)

制約2：アンケートに答えた日だけ参加できる

アンケートに含まれない日は、必ず0という制約を付与します

for i in range(n):
  for d in range(event_day_num):
    if not d in attendance_list[i]:
       model.Add(date_of_attendance[i][d] == 0 )

制約３：各開催日の収容人数を超えない

会場の収容人数の制約を付与します。

for d in range(event_day_num):
     model.Add(sum([
         date_of_attendance[i][d]
         for i in range(n)
     ]) <= capacity[d])

最適化指標：希望優先順がなるべく上の日を選ぶ

希望日の優先順は、「できる限りXXXしたい」という表現になっていて
明確な制約にはなっていないません。
このような場合は、評価関数を定義してその評価関数が最小（最大）となるよう設定します。
今回は、評価関数としてスコアテーブルを定義して合計スコアが最大となるよう制約を付与しました。

score_table = [16,8,4,2,1] # 優先順が落ちると、価値は半減していくと想定
priority_table = [1,2,3,4,5] # 後で表示に使う
# 各人のスコアテーブルを作成
score_table_per_man = []
priority_table_per_man = []

for i in range(n):
  s = [0] * event_day_num
  pt = [0] * event_day_num
  for p in range(len(attendance_list[i])):
    attend_day = attendance_list[i][p]
    s[attend_day] = score_table[p]
    pt[attend_day] = priority_table[p]
  score_table_per_man.append(s)
  priority_table_per_man.append(pt)
  
model.Maximize(sum([
    score_table_per_man[i][d] * date_of_attendance[i][d] 
    for d in range(event_day_num) 
    for i in range(n) 
]))

ソルバー起動！

解があれば、statusがOPTIMALになります。
無事、解けたようです。

solver = cp_model.CpSolver()
status = solver.Solve(model)
# 解の確認
print("status:", solver.StatusName(status))

# 結果出力
# for i in range(n):
#   print([solver.Value(date_of_attendance[i][j]) for j in range(event_day_num)  ])

# スコア合計
print("TotalScore",sum([
    score_table_per_man[i][d] * solver.Value(date_of_attendance[i][d])
    for d in range(event_day_num) 
    for i in range(n) 
]))

結果

status: OPTIMAL
TotalScore 1472

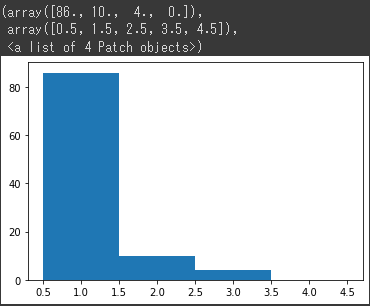
100人中、86人が第一候補になっており、大体良い結果といえます

import matplotlib.pyplot as plt
plt.hist([
    sum([priority_table_per_man[i][d] * solver.Value(date_of_attendance[i][d]) for d in range(event_day_num)])
    for i in range(n)
], bins=[0.5,1.5,2.5,3.5,4.5])

シンプル解法で解いて比較

制約が厳しい順にソートして割当てていく（Greedy戦略）で解いてみます
こちらでも問題無く解けました

def comparerer(x):
  score = len(x) # 参加可能な日が少ない人が優先
  for i in x:
    if i <= 1: # 大会場だったらスコア加算して優先度を下げる
      score += 0.1
  return score

attendance_list_ordered = sorted(attendance_list, key=comparerer)
attend_days = []
rest_capacity = list(capacity)

for x in attendance_list_ordered:
  can_attend_capacity = [ (i,c) for i,c in  enumerate(rest_capacity) if i in x]
  attend_day = max(can_attend_capacity,key=lambda i: i[1])[0] # 残り許容人数が多い会場に優先的に行く
  rest_capacity[attend_day] -= 1
  if max(rest_capacity) < 0:
    print("Not Feasible")
    break
  attend_days.append(attend_day)
attend_days

結果

[4, 3, 3, 4, ...

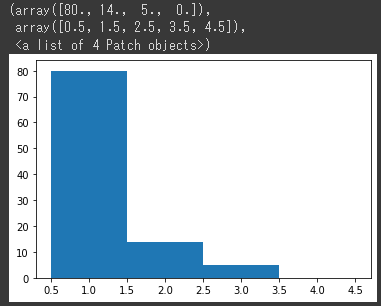
しかし、若干結果は悪く、第一希望の人は80人となりました。

priority_list = [j.index(i)+1 for i,j in zip(attend_days,attendance_list_ordered)]
plt.hist(priority_list, bins=[0.5,1.5,2.5,3.5,4.5])

すきなラーメン

長浜屋台 一心亭 本店です。
スタンダードな長浜ラーメン。かためんで！