はじめに
最も単純な線形回帰モデルに最小二乗法があります。その派生として正則化項を目的関数に加えて最適化を行うRidge回帰やLasso回帰があります。正則化項を加えることでオーバーフィッティングをやわらげたり、スパースな推定ができたりします。スパースな推定とは、求める回帰係数を0と予測することを言います。目的変数に関係のない変数を落としてくれるのですね。すごい。
さて、本記事ではLasso回帰の派生であるFused Lassoについて簡単に説明し、その後Rで実装したいと思います。
回帰問題
回帰問題の設定を説明します。標準化された目的変数$y$と$p$次元の説明変数$\underline{x}$のペアデータ$(y,\underline{x})$が$(y_1,\underline{x}_1),(y_2,\underline{x}_2),\dots,(y_n,\underline{x}_n)$の$n$個得られたとします。$\underline{x}_i(i=1,2,\dots,n)$は$p$次元ベクトルで
\underline{x}_i
=
\begin{pmatrix}
x_{i1}\\
x_{i2}\\
\vdots\\
x_{ip}
\end{pmatrix}
を意味します。説明変数$\underline{x}$を用いて$y$を予測する問題を考えます。$y$が「みかん」や「りんご」などを表し0や1などで表せる場合には分類問題、$y$がお店の売り上げのような数値をとる場合には回帰問題と呼びます。本記事では、後者の回帰問題を想定しています。
さて、「説明変数$\underline{x}$を用いて$y$を予測する」とお話しましたが、$y$と$\underline{x}$に
y=\underline{\beta}^T\underline{x} + \varepsilon
という構造を持つと仮定します。よくみる線形回帰モデルですね。ここで、$\underline{\beta}$は
\underline{\beta}
=
\begin{pmatrix}
\beta_{1}\\
\beta_{2}\\
\vdots\\
\beta_{p}
\end{pmatrix}
です。$\varepsilon$は誤差項で、データはノイズがのって観測されているという考えに基づいています。切片項については、データは標準化されたものを考えているので切片項を無視できます。これについて知りたい方はこの記事を引用しておきますのでご覧ください。
ここまでを簡単に整理すると、目的変数$y$を$\underline{\beta}^T\underline{x}$を用いて予測することになり、$\underline{\beta}$さえ求めればよいことになります。ここで、$y$と$\underline{\beta}^T\underline{x}$の差の2乗、つまり、誤差二乗和が最小となるような$\beta$を求める手法を最小二乗法といいます。その解$\hat{\underline{\beta}}$は
\hat{\underline{\beta}}
=
\underset{\beta}{\arg\min}~~\sum_{i=1}^n \left(y_i-\sum_{j=1}^{p}\beta_j x_{ij}\right)^2
と表されます。$\arg\min$というのは、最小にするようなものという意味の記号ですので、誤差二乗和を最小にするようなものが$\hat{\underline{\beta}}$だといっている訳です。また、最小化される関数を目的関数とも言います。
最小二乗法の問題とRidge回帰・Lasso回帰
最小二乗法には次の問題があります。
- 説明変数間に相関がある場合には解が求まらない(多重共線性)
- データ数($n$)よりもデータの次元($p$)が大きい場合($n<p$)の時に解が求まらない
- はずれ値に対してその影響を強く受けてしまう
- 過学習を起こしやすい
これらの問題を解決しようとするのが、Ridge回帰になります。Ridge回帰は最小二乗法の目的関数に$\ell$2正則化項を加えることにより、回帰係数を求める手法になります。また、どの説明変数が目的変数に利いているのかをみたいときがあります。それに対する手法がLasso回帰です。Lasso回帰は最小二乗法の目的関数に$\ell$1正則化項を加えたものになります。Ridge回帰やLasso回帰で得られる解はそれぞれ
\begin{align*}
\hat{\underline{\beta}}_{\text{Ridge}}
&=
\underset{\beta}{\arg\min}~~\left\{\sum_{i=1}^n \left(y_i-\sum_{j=1}^{p}\beta_j x_{ij}\right)^2+\lambda\sum_{j=1}^{p}\beta_j^2\right\},\\
\hat{\underline{\beta}}_{\text{Lasso}}
&=
\underset{\beta}{\arg\min}~~\left\{\sum_{i=1}^n \left(y_i-\sum_{j=1}^{p}\beta_j x_{ij}\right)^2+\lambda\sum_{j=1}^{p}\left|\beta_j\right|\right\}
\end{align*}
と表されます。ここで、$\lambda(>0)$は正則化パラメータと呼ばれるもので正則化の度合いを調整するハイパーパラメータとなっています。Ridge回帰やLasso回帰はインターネット上にたくさん記事がありますので、詳細はそちらにお任せします。
Fused Lasso
Lasso回帰の派生形としてFused Lassoがあります。それは次のような特徴があります。
- 隣り合う説明変数同士の回帰係数を同じ値になるよう推定する
- Lassoと同じようにスパースに推定する
説明変数に順序があり、ある説明変数に着目したときにその説明変数の前後の回帰係数を同じにしたいときに使われ、時系列データや画像データなどに適用されるようです。
Fused Lassoの目的関数
Fused Lassoの目的関数は
\begin{equation}
\sum_{i=1}^n \left(y_i-\sum_{j=1}^{p}\beta_j x_{ij}\right)^2
+\lambda\sum_{j=1}^{p-1}\left|\beta_j-\beta_{j+1}\right|
+\gamma\lambda\sum_{j=1}^{p}\left|\beta_j\right| \tag{1}
\end{equation}
として与えられます。第一項目は誤差二乗和、第二項目が隣合う説明変数の回帰係数が同じになるような正則化項、第三項目がLasso回帰と同じ$\ell$1正則化項でスパース性に関する項です。また、$\lambda(>0),\gamma(\geq 0)$はハイパーパラメータになっています。この目的関数を最小化するアルゴリズムとして、Dual Path Algorithmがあり、
が参考になります。
実装
Fused LassoをRで実装していきたいと思います。genlassoパッケージを使うのですが、そのパッケージでは、
\frac{1}{2}\sum_{i=1}^n \left(y_i-\sum_{j=1}^{p}\beta_j x_{ij}\right)^2
+\lambda\|D\underline{\beta}\|_1
+\gamma\lambda\|\underline{\beta}\|_1
という目的関数を想定しています。ここで、$||\cdot||_1$は$\ell$1ノルムを表しています。ベクトルの各成分の絶対値の和のことです。行列$D$を対角成分が1、その右隣が-1、それ以外が0の行列、つまり
D=
\begin{pmatrix}
1&-1&0&0&\dots&0&0\\
0&1&-1&0&\dots&0&0\\
&&&&\ddots&\\
0&0&0&0&\dots&-1&1\\
\end{pmatrix}
とおくと、(1)とほとんど同じになります。ほとんどというのは第一項目に$1/2$があるかないかの差を意味しており、これは最適解への影響はありません。よって、この行列$D$を作成しシミュレーションする必要があります。
いよいよ、簡単なシミュレーションをしていきます。まずは設定です。
- データ数:100
- 説明変数:7次元で、すべて標準正規分布から乱数を生成します。すなわち、
$$x_{ij}\overset{\text{i.i.d.}}{\sim} N(0,1),i=1,2,\dots,100,j=1,2,\dots,7$$
です。$\text{i.i.d.}$は独立同分布に従うということを意味しています。
- 誤差:標準正規分布から乱数を生成します。すなわち、
$$\varepsilon_{i}\overset{\text{i.i.d.}}{\sim} N(0,1),i=1,2,\dots,100$$
です。
- 真の構造:目的変数$y$は$x_1$と$x_2$のみに依存し、
$$y=0.5x_1+0.5x_2+\varepsilon$$
のように仮定する。
以上の設定で、実装していきます。各コードはコメントアウトで記載しています。
# genlassoパッケージを使うので、インストールしましょう
# install.packages("genlasso")
# genlassoパッケージの読み込み
library(genlasso)
# ランダムシード値を固定しています
set.seed(7)
n <- 100 #データの個数
p <- 7 #データの次元数
X <- matrix(rnorm(n*p,0,1),n,p) #説明変数の生成
e <- rnorm(n,0,1) #誤差項の生成
y <- scale(0.5*X[,1]+0.5*X[,2] + e) #目的変数の作成
D <- cbind(diag(-1,p-1),rep(0,p-1)) + cbind(rep(0,p-1),diag(1,p-1)) #行列Dの作成
model <- fusedlasso(y, X, D=D, gamma=1) #モデル構築
model$beta #回帰係数の表示
回帰係数を表示させた結果は次のようになります。一番上の行の数字は正則化パラメータ$\lambda$の値を表しています。あらゆる$\lambda$で回帰係数を求めています。
> model$beta
32.984 30.734 26.225 11.651 10.752 8.768 5.39 3.95 3.522 1.586 0.925 0.879 0.687 0.627 0.543
[1,] 0 0 0 0.2310796 0.2453327 0.2767797 0.2735293 0.271453972 0.26866067 0.25836220 0.25307380 0.25270276 0.251066889 0.25055674 0.248773641
[2,] 0 0 0 0.2310796 0.2453327 0.2767797 0.3884035 0.433890253 0.44695311 0.50219862 0.52397779 0.52550586 0.531626543 0.53353529 0.537616136
[3,] 0 0 0 0.0000000 0.0000000 0.0000000 0.0000000 0.006258884 0.00000000 0.00000000 -0.02146425 -0.02297023 -0.028528979 -0.03026249 -0.032714430
[4,] 0 0 0 0.0000000 0.0000000 0.0000000 0.0000000 0.006258884 0.01715739 0.06428347 0.08202322 0.08326789 0.088478562 0.09010353 0.092063011
[5,] 0 0 0 0.0000000 0.0000000 0.0000000 0.0000000 0.000000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0.00000000 -0.004290770
[6,] 0 0 0 0.0000000 0.0000000 0.0000000 0.0000000 0.000000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0.00000000 0.000000000
[7,] 0 0 0 0.0000000 0.0000000 0.0000000 0.0000000 0.000000000 0.00000000 0.00000000 0.00000000 0.00000000 0.003366362 0.00441617 0.006214238
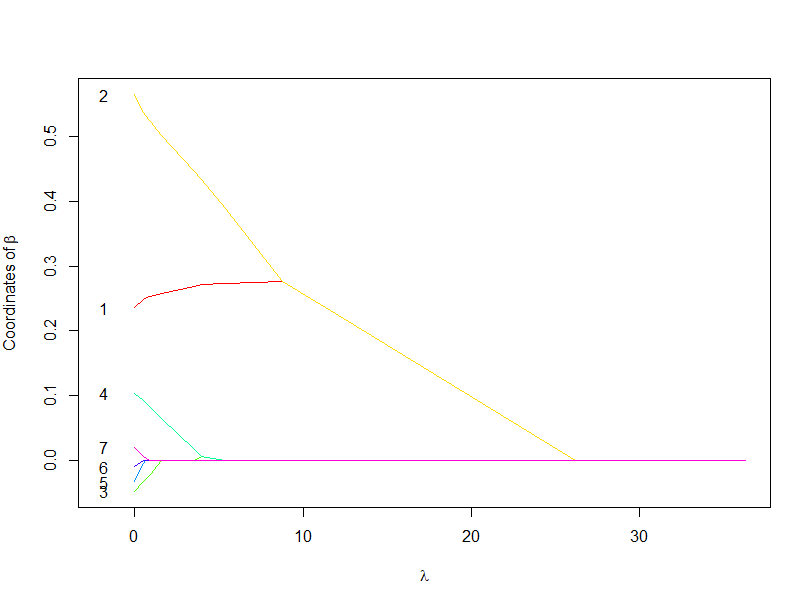
続いて、解パス図を描画します。解パス図は$\lambda$の値によって得られる回帰係数の変化をグラフにした図です。
plot(model,numbers=TRUE,vlines = FALSE) #Path図の描画
解パス図より、目的変数$y$に利いている$x_1,x_2$は他の説明変数よりも$\lambda$が大きくなっていも残っていることがわかります。逆に$y$に利いていない変数は早めに0に落ちて、$y$との関係を遮断するようにしています。そのため、$\lambda$の設定が大切になってきます。
また、$x_1,x_2$の推定された係数はどの$\lambda$でも真の回帰係数の0.5を予測できていません。シミュレーションの設定が悪いのか、そもそも使い方が悪いのか、さらなる調査が必要そうです、
さいごに
回帰問題の説明からFused Lassoの説明とRでの実装を行いました。解パス図は良い感じでしたが、回帰係数の予測はあまりできませんでした。回帰係数の推定より、説明変数の選択の意味合いが強いのかもしれません。Lassoの派生形は他にもGroup Lassoなどあるようです。「正則化項の加え方でどのように推定したいのかを考慮できる」ということを感じられたことは面白いなと思いました。
参考文献
(原著)https://web.stanford.edu/group/SOL/papers/fused-lasso-JRSSB.pdf
(R実装)https://rdrr.io/cran/genlasso/man/fusedlasso.html