はじめに
こんにちは,Umamusume22です.前回,投稿した記事では魔法陣グルグルの魔法陣は一筆書きができるか検証するという内容でした.トーラとトカゲのシッポをピックアップしました.以下は前回の記事のURLです.
今回は引き続き前回と同様にトーラとトカゲのシッポはハミルトングラフに該当するか検証します.私の身内だけかもしれませんが意外に魔法陣グルグルの存在を知っている人が多かったです.しかし,少し古い漫画なので詳しく知っている人はほとんどいませんでした.私は実家に漫画があるので読んでいます.一応,魔法陣グルグルのpvのURLも貼ってきおきます
ハミルトングラフとは?[1,2]
グラフ理論は前回の記事で解説したため,省略します.ハミルトングラフとは全ての点を一度だけ通過して元に戻れるグラフのことを指します.
ディラック(Dirac)の定理[1,2]
ディラックの定理とは
$$
d\big(v)\geqq \frac{1}{2}n\tag{1}
$$
に当てはまる数式のことです.なお,$n$は3つ以上の点があるグラフの点の数,$v$は全ての頂点の数を表します.あるグラフの最小次数$d$($v)_{min}$と点の数$n$は
$$
2・d\big(v)_{min}\geqq n\tag{2}
$$
となります.つまり,数式(2)よりあるグラフの頂点において点の数が最小次数の2倍以下になればハミルトングラフが成立します.
オーレの定理[1,2]
オーレの定理とはあるグラフの頂点において隣接していない2点の次数の合計値が頂点数以上であればハミルトングラフの条件を満たすというものです.隣接していない2点の頂点は任意で選びます.2頂点の決め方に決まりはありません.ちなみにオレオの定理でもオレの定理でもありません笑
頂点の数が$n$のグラフの任意の隣接していない2点$u$,$v$に対して
$$
d(u)+d(v) \geqq n\tag{3}
$$
を満たすグラフはハミルトングラフが成立します.
オイラーグラフとハミルトングラフの違い[1,2]
前回,書いた記事でオイラーグラフが出てきました.ここでもう一度オイラーグラフとハミルトングラフの違いを再確認したいと思います
オイラーグラフ
オイラーグラフとは辺を一度だけ通って始点と終点が一致するグラフのことです.
以下はオイラーグラフの例です.頂点が6つある図形を与えて一筆書きを行います
右下の頂点から矢印の向きに一筆書きを行った結果,全ての辺を一度だけ通過することが出来ました.また,始点と終点も一致しています.このようなグラフがオイラーグラフです.個人的に好きなグラフです.
ハミルトングラフ
ハミルトングラフとは全ての頂点を一度だけ通って始点と終点が一致するグラフのことです.
以下はハミルトングラフの例です.頂点が4つある図形を与えて一筆書きを行います
頂点の右下→頂点の左下→頂点の右上→頂点の左上→頂点の右下の順番に辺を通過することで始点と終点が一致しました.全ての頂点を一度だけ通過することは出来ましたが全ての辺は通ることが出来ませんでした.このように全ての頂点を一度だけ通過し,始点に戻ることが可能なグラフをハミルトングラフと呼びます.
オイラーグラフとハミルトングラフの両方に該当するグラフの例
オイラーグラフとハミルトングラフの違いの例でも紹介したグラフです
全ての辺と頂点を一度で通過することが出来ました.始点と終点も一致してます.
上記のグラフはオイラーグラフとハミルトングラフの両方に該当します.
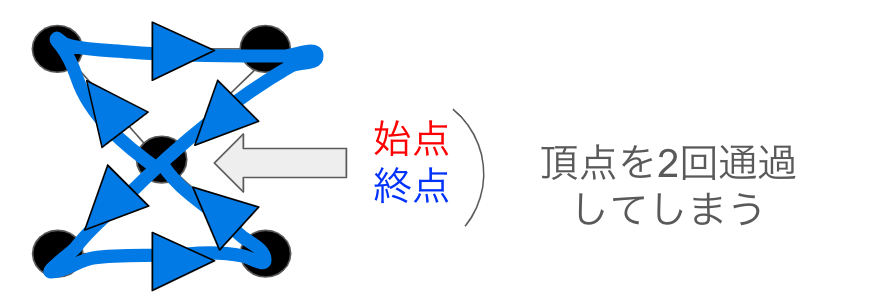
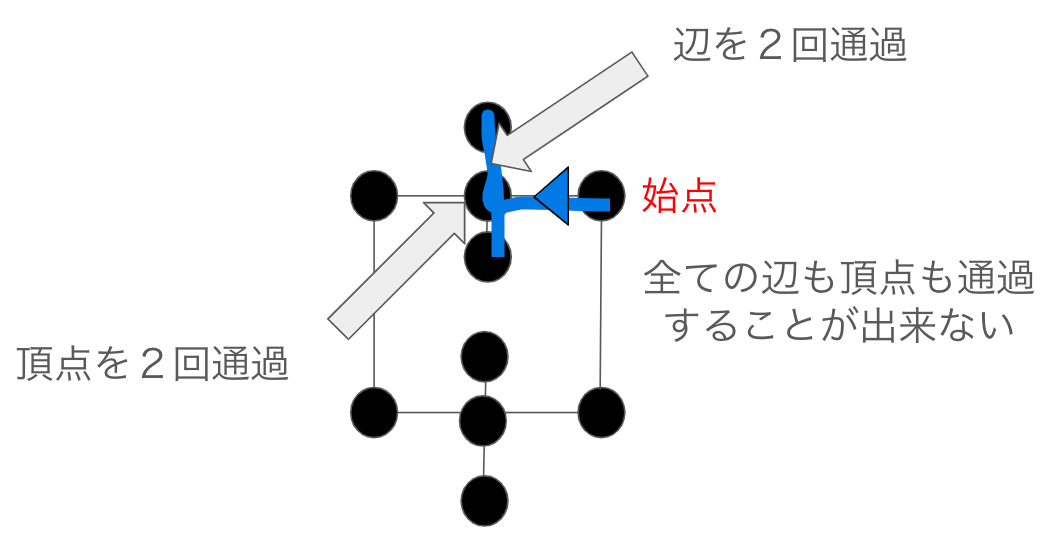
オイラーグラフのみ該当するグラフの例
次にオイラーグラフのみ該当するグラフを紹介します.
真ん中の頂点→左下の頂点→右下の頂点→真ん中の頂点→左上の頂点→右上の頂点→真ん中の頂点の順番に一筆書きを行うことで全ての辺を通過することが出来ました.始点と終点も一致しています.
しかし,真ん中の頂点を2回通過してしまうのでハミルトングラフには該当しません.
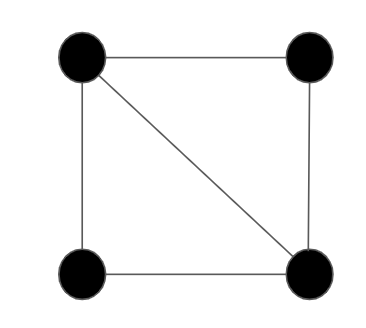
ハミルトングラフのみ該当するグラフの例
次にハミルトングラフのみ該当するグラフを紹介します.
右上の頂点→左上の頂点→左下の頂点→右下の頂点の順番に一筆書きを行うことで全ての頂点を通過することが出来ました.始点と終点も一致してます.しかし,左上の頂点から右下の頂点まで描かれている辺を通過することが出来ません.もし,真ん中の辺を通過するように一筆書きを行った場合,始点に戻ることが出来ません.
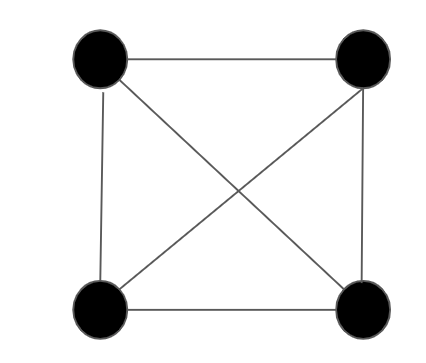
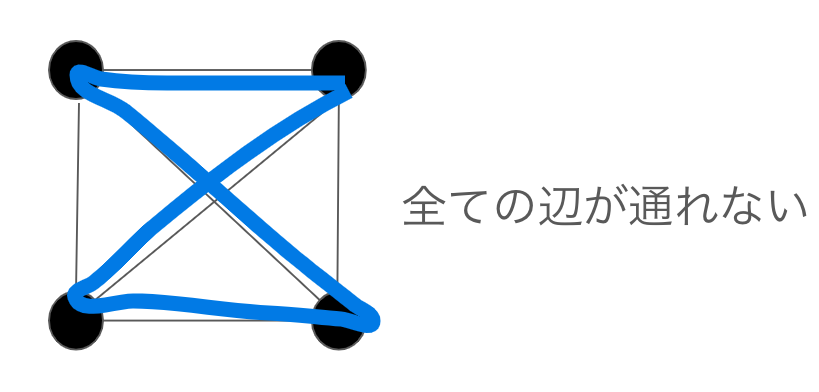
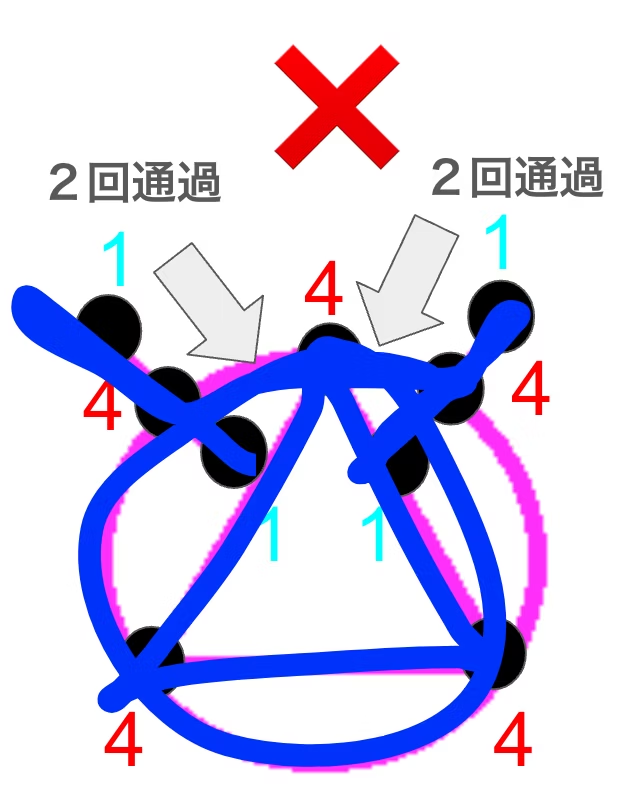
オイラーグラフもハミルトングラフにも該当しないグラフの例
最後にオイラーグラフもハミルトングラフにも該当しないグラフを紹介します.

右上の頂点を始点に青の三角形の方向に向かって一筆書きを行いましたが全ての辺,頂点も通過することが出来ませんでした.原因は辺の真ん中に縦線が存在するからです.右上と左上の頂点間,右下と左下の頂点間の辺にそれぞれ縦線が引かれています.縦線の存在によって奇点が生じてしまい,縦線の真ん中の頂点も2回通過することになってしまいます.
ピックアップした2つの魔法陣はハミルトングラフに該当するか検証[1,2,3]
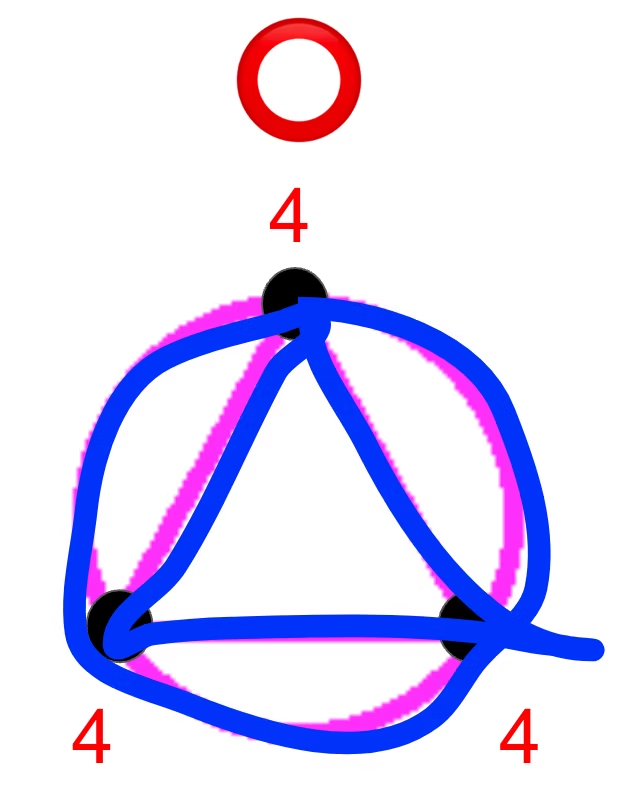
魔法陣:トーラ
出典:"魔法陣紹介!",https://hp.vector.co.jp/authors/VA019204/guru/mahouzin.htm
再びトーラの登場です.上記の画像がトーラです.トーラは魔法陣グルグルの最初に出てくる呪文です.火が垂直に出るのが特徴です.
出典:"魔法陣グルグルの魔法・グルグル・キラキラまとめ",https://renote.net/articles/7732
トーラの検証結果
ディラックの定理
$$
2・d\big(v)_{min}\geqq n
$$
にトーラの最小次数$d(v)_{min}$と頂点数$n$を代入すると
$$
8(最小次数) \geqq 3 (頂点数)
$$
となります.
オーレの定理
トーラには隣接していない2点の頂点がありません.どの頂点も隣接しています.オーレの定理は使えませんでした.
魔法陣:トカゲのシッポ

出典:"魔法陣紹介!",https://hp.vector.co.jp/authors/VA019204/guru/mahouzin.htm
続いてトカゲのシッポの登場です.著者が魔法陣グルグルを漫画で読んだ時に一番印象的だった呪文です.ククリが使った呪文です.この呪文も敵に火を与えます.トカゲのシッポーーーーーーーー!!! (しつこい)

出典:"ピクシブ百科事典",https://dic.pixiv.net/a/%E3%83%88%E3%82%AB%E3%82%B2%E3%81%AE%E3%81%97%E3%81%A3%E3%81%BD
トカゲのシッポの検証結果
ディラックの定理
$$
2・d\big(v)_{min}\geqq n
$$
にトーラの最小次数$d(v)_{min}$と頂点数$n$を代入すると
$$
2(最小次数) \geqq 9 (頂点数)
$$
となります.
ハミルトングラフは不成立です.
オーレの定理
トカゲのシッポには隣接していない頂点があります
$$
d(u)+d(v) \geqq n
$$
にトカゲのシッポの最小次数$d(v)_{min}$と頂点数$n$を代入すると
$$
2 \geqq 9
$$
オーレの定理にも非該当でした.ハミルトングラフは不成立です.
最後に
トーラはハミルトングラフでしたがトカゲのシッポは非該当でした.トーラはディラックの定理とオーレの定理に当てはまりました.しかし,トカゲのシッポは二つの定理の条件に該当しませんでした.トカゲのシッポの円上に二つの直線が入っているのが原因だと考えられます.
今後は他の魔法陣もオイラーグラフやハミルトングラフに該当するか検証して行きたいと思います.また,ソースコードを書いて与えた魔法陣の偶点数やどんなグラフに該当するか自動で判定することを目指します.
ここまで記事を読んでいただきありがとうございました!
※ウマ娘の声をフーリエ変換した記事や水栓の開閉判定をLineに通知する記事も書いています.suzuが私です.興味がある方はぜひご覧ください!
https://vigne-cla.com/31-1/#toc5
※noteも始めました.
https://note.com/madoka235/n/nbba2153326e1
ぜひフォローよろしくお願いします!
参考文献
[1] "うさぎでもわかる離散数学(グラフ理論) 第10羽 一筆書きができるかの簡単な見つけ方・オイラーグラフ・ハミルトングラフ"
https://www.momoyama-usagi.com/entry/math-risan10#i-2
[2] "ハミルトン閉路"
https://school.gifu-net.ed.jp/ena-hs/ssh/H29ssh/sc3/31701.pdf
[3] "魔法陣紹介!"
https://hp.vector.co.jp/authors/VA019204/guru/mahouzin.htm