OpenModelicaで偏微分方程式を解く機能
いつ頃からか(多分OpenModelica1.12とか）OpenModelicaで偏微分方程式を解く機能が実装されました。
Modelica Conferenceなどでは発表がありましたが実はそんなに宣伝されていませんでした。
勉強会でネタないかなーとOpenModelicaのドキュメントをあさっていると正式にUser Guideが整っていたのでとりあえず確認してみました。
偏微分方程式機能の名前はPDEModelicaという名称でModelica Specificationには無い機能をOpenModelicaで実装しているようです。
User Guide
https://openmodelica.org/doc/OpenModelicaUsersGuide/latest/pdemodelica.html
偏微分方程式機能(PDEModelica)で出来ること
偏微分方程式を解く、といっても解けるのは時間項ともう一つ任意独立変数の2変数偏微分方程式です。
三次元（x,y,z)を期待してはいけません。
また書いてはいませんが、元の論文からすると差分法を使っています。
設定方法
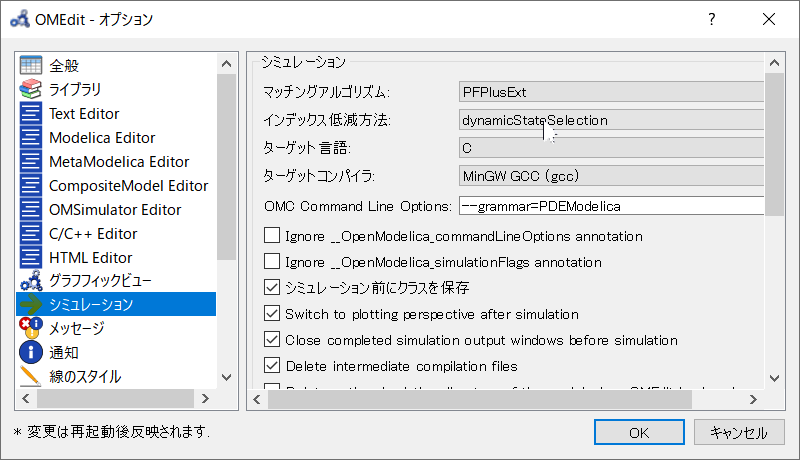
1.OpenModelicaを開いて「ツール」->「オプション」を開いてください。
2.「シミュレーション」をクリックし、「OMC Command Line Options」へ「--grammar=PDEModelica」と記入してください。
例題
どんな方程式を解くか
以下のような方程式が例題として載っています
上記の方程式は図でいうと以下のようになります。
Modelicaコード
解説
3行目
parameter DomainLineSegment1D omega(L = 1, N = 100) "domain";
DomainLineSegment1Dは領域を定義する型。
いわゆる独立変数
Lが長さ、Nが分割数
4行目
field Real u(domain = omega) "field";
fieldは解きたい場を定義する型
いわゆる従属変数
5-6行目
initial equation
u = sin(2*pi*omega.x) "IC";
初期場の定義
DomainLineSegment1D内にxという変数があるのが分かる
ICはInitial Conditionの略
8行目
der(u) + pder(u,x) = 0 indomain omega "PDE";
解きたい偏微分方程式
indomain omega と方程式の後についているのが特徴的
決して記述ミスじゃないので消さないように
（最初消してしまって動きませんでした。。。）
9行目
u = 0 indomain omega.left "BC";
境界条件
10行目
u = extrapolateField(u) indomain omega.right "extrapolation";
境界条件を定義していない方の境界面を定義するためのおまじないと覚えておけばよいと思う
一応、User GUideの記述を引用する
All fields that are spatially differentiated must have either BC or extrapolation at each boundary. This extrapolation should be done automatically by the compiler, but this has not been implemented yet. The current workaround is the usage of the extrapolateField() operator directly in the model.
要は本来コンパイラが自動的にやるべきことだが、まだ実装してないから自分で書いてね、ということだと思う
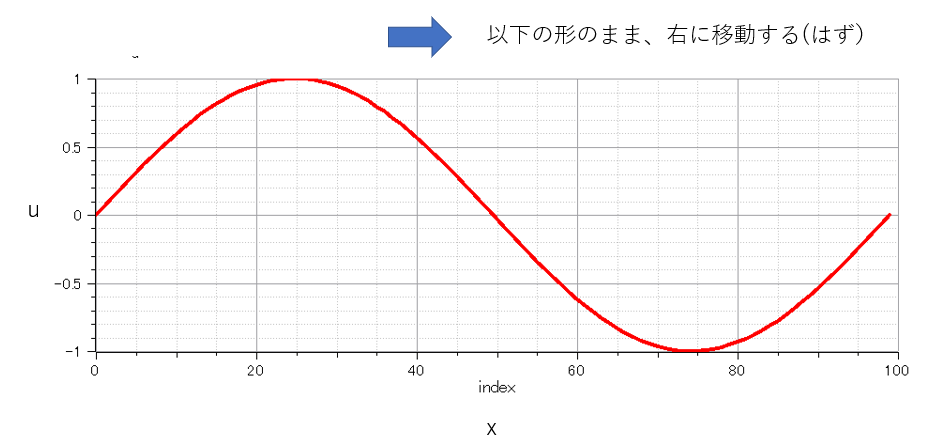
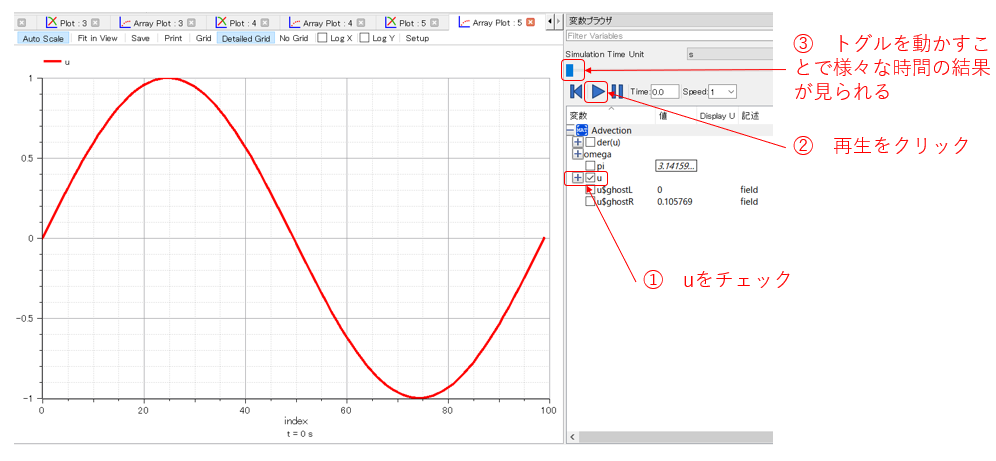
計算結果
以下のようにプロットウィンドウを操作するとアニメーションで結果が表示されます
0.25sec
振動しているような
0.50sec
やっぱり振動している
1.0sec
振動が消えず残っている
矩形波で計算
勉強会で矩形波で計算すると精度の評価を適切に出来るとご助言頂いた。
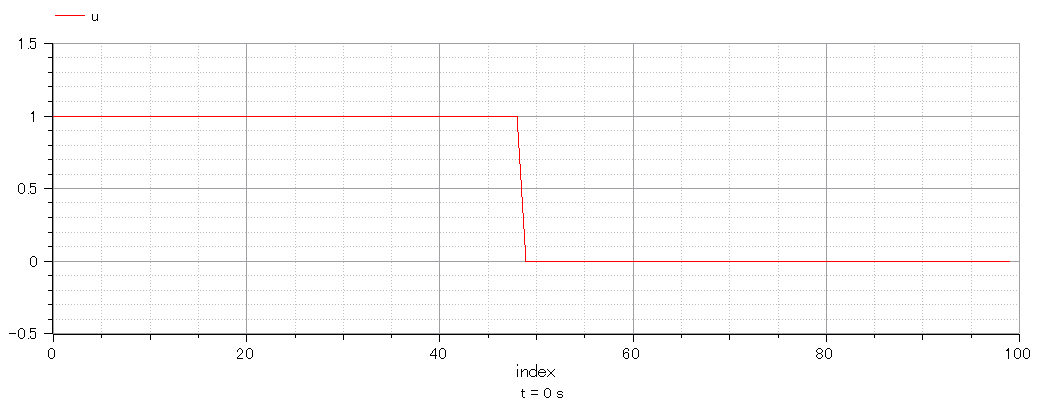
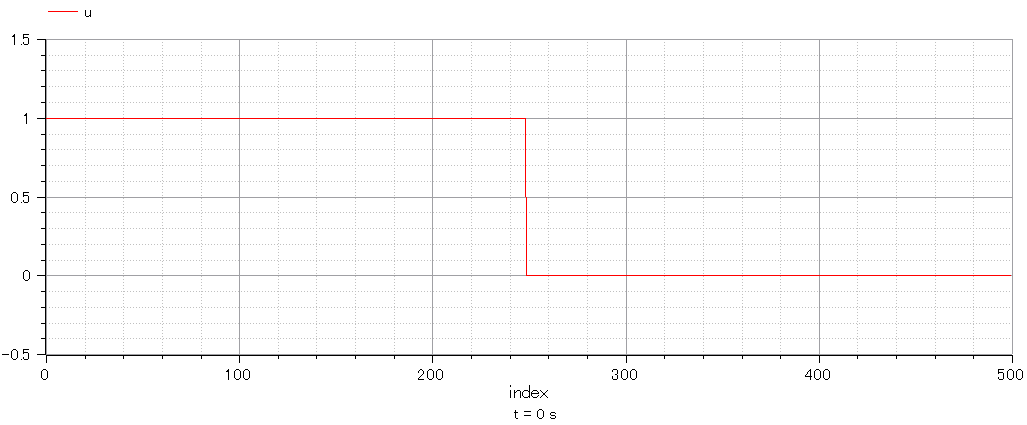
そこで以下のような初期値で計算を実施した。
綺麗な矩形にならなかったが。。。
初期状態
0.05sec ああ・・・
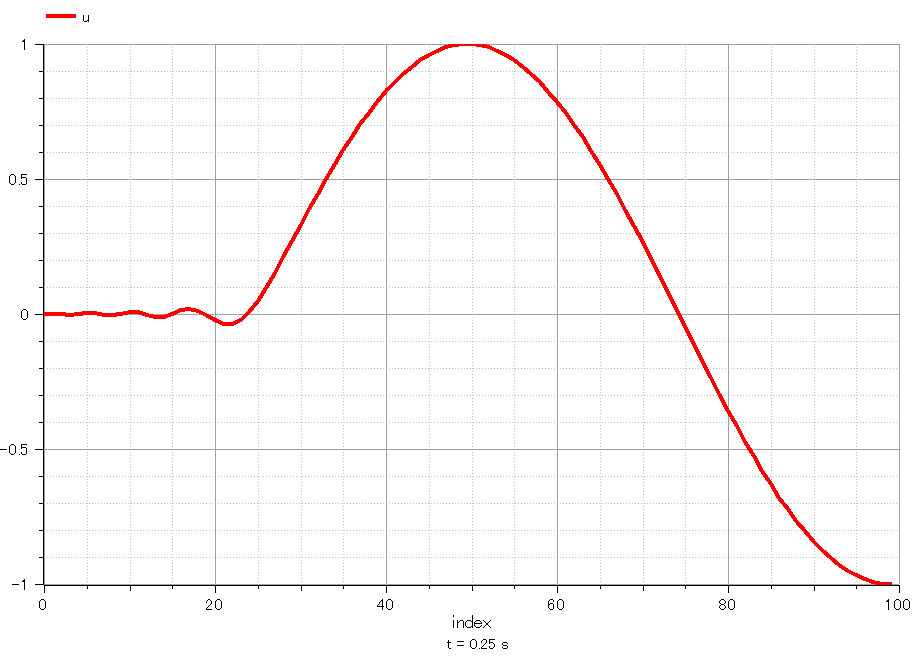
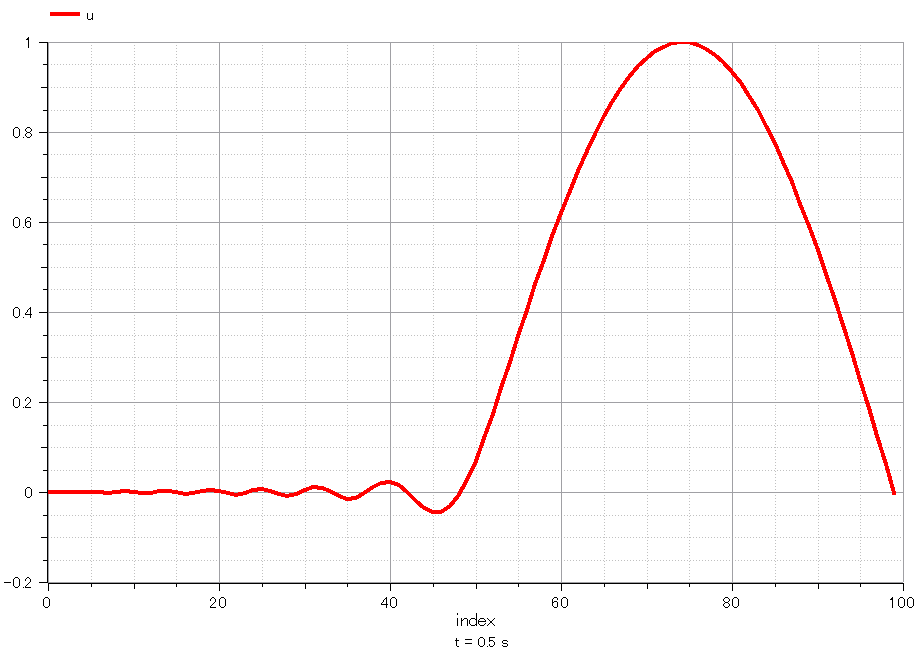
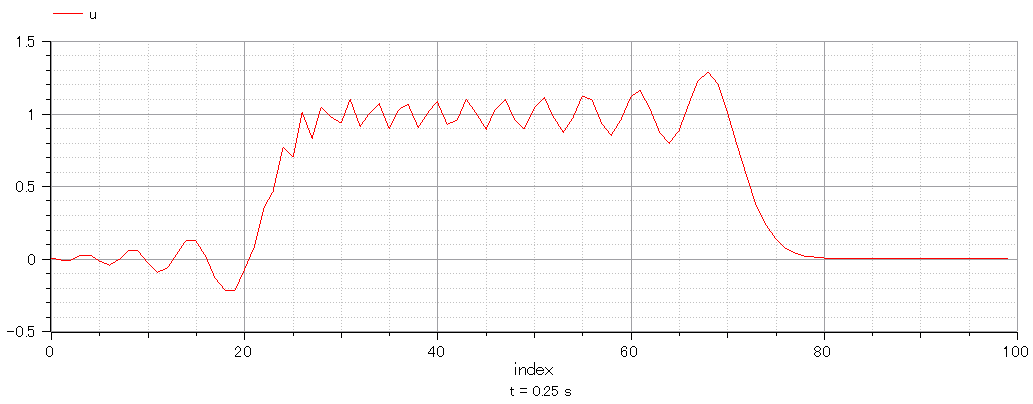
0.25sec
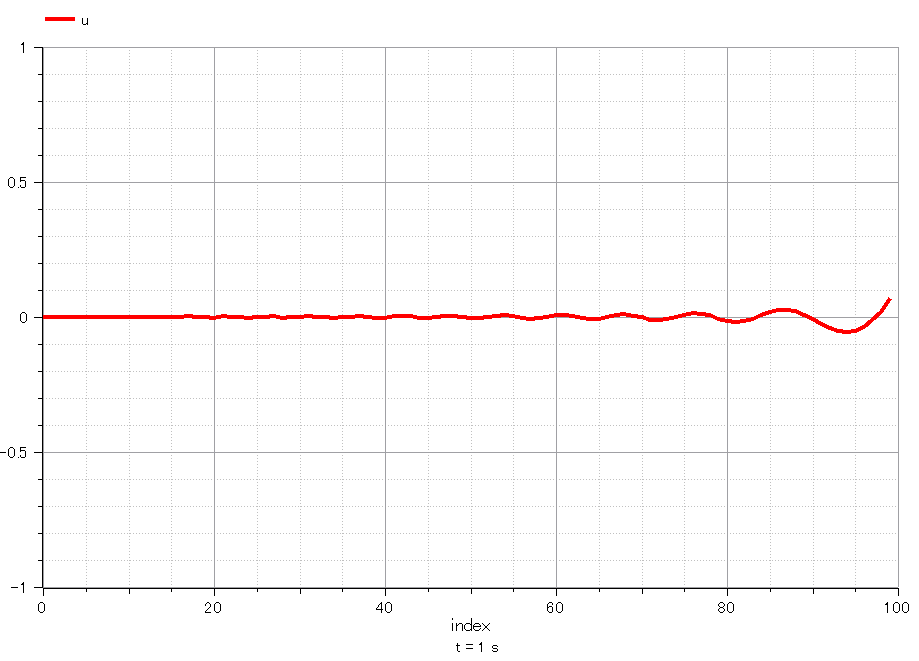
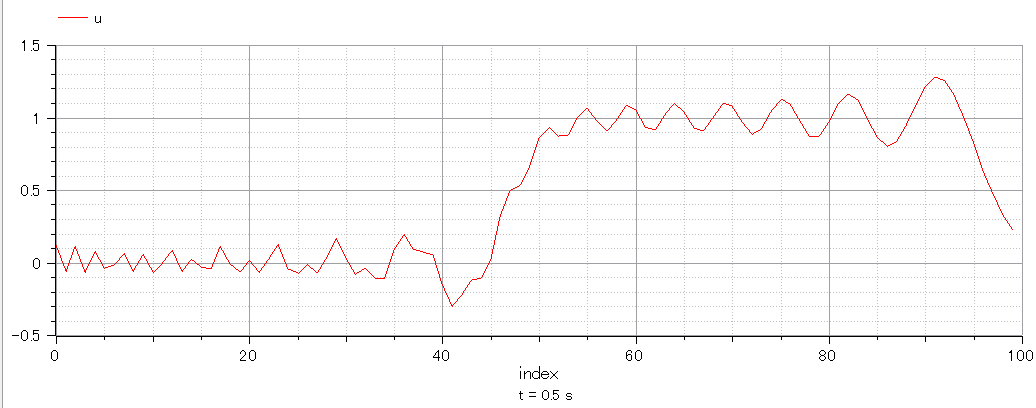
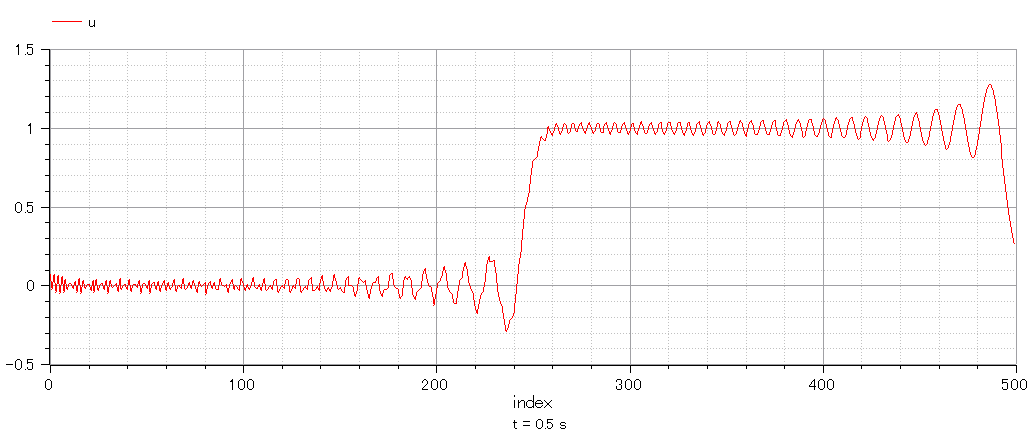
0.50sec
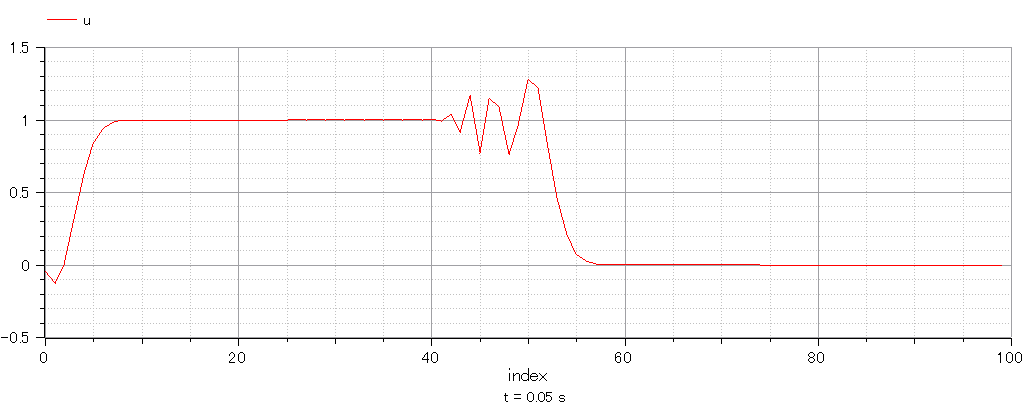
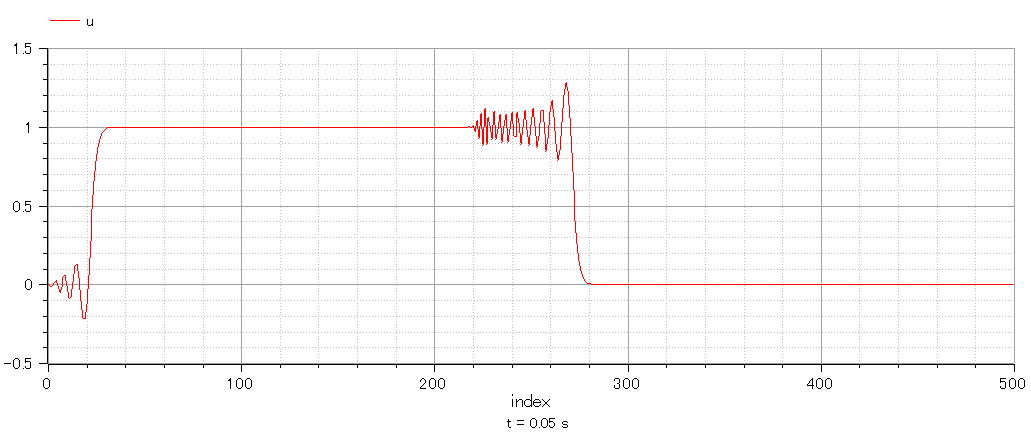
分割数N=500にして再計算
初期状態 今回は矩形波のようになっている
0.05sec
0.50sec
精度が悪いようだ
所感
矩形波を試していない時
少し精度が気になるがまぁ解けたという感じ
矩形波を試した後
これは精度や計算的な不安定性からあまり使わない方がよさそう・・・
感想
元論文では中央差分、前進差分、後退差分程度が実装されていたと思うのでそこらへんが選べるようになるといいかもしれない
ただ、正直上記の機能程度なら自分で書いてしまえるのでなんとも。
(一次元非定常熱伝導方程式を実装した時の資料は以下
https://www.slideshare.net/ssusere33bfb/170624-room-andmbdandislideshare)
ただし、Modelica界隈が常微分だけでなく偏微分も取り組んでいることが分かる熱いメッセージだと思えば非常にわくわくする機能だと思う