前回の記事で機械学習の全体的な分類についてまとめたので今回からはそれぞれの具体的な実装について記して行く。
前回の記事はこちらから
https://qiita.com/U__ki/items/4ae54da6cadec8a84d1b
単回帰分析の実装
今回のテーマは、
「部屋の大きさにあうテレビサイズは?」です。
春から引越しが決まっている人もいるのでないでしょうか。
新しい部屋の大きさにふさわしいテレビのサイズをどうやって決めようかと思う人のために部屋の大きさにあうテレビサイズを単回帰分析を用いて求めてみたいと思う。
せっかくなのでpandasを用いて模擬データを作成し、そのあとそのデータを基にして分析することにした。
pandasによるcsvファイル作成
まずこちらの記事(https://www.olive-hitomawashi.com/lifestyle/2019/10/post-294.html) を参考に部屋のサイズにあうオススメのテレビサイズのデータを以下のようにした。
(これあるならこの記事いらなくない)
【テレビサイズ】
6乗: 24インチ
8畳: 32インチ
10畳: 40インチ
12畳: 50インチ
このデータをpandasを用いてcsvファイルとして出力する。
# csv作成pandas
import pandas as pd
df=pd.DataFrame([
["6", "24"],
["8", "32"],
["10", "40"],
["12", "50"]],
columns=["room_size", "tv_inch"]
)
df.to_csv("room_tv.csv", index=False)
dfはdata flameの略。
またindex=Falseとすることでcsv内のインデックス番号を無くした。
これで同一フォルダ上に新しくroom_tv.csvというファイルが作成された。
以上でフォルダの中に以下のファイルが生成されていたら成功だ。
room_size,tv_inch
6,24
8,32
10,40
12,50
これで今回用いるcsvファイルが用意できた。
単回帰分析
続いて今回のメインである単回帰分析を行っていく。
単回帰分析は次の3つの構成となる。
・モデルの決定
・評価関数を設定する
・評価関数を最小化する(傾きの決定)
モデルの決定
まずcsvを読み込む。
df=pd.read_csv("room_tv.csv")
これでjupyter notebookを用いているなら以下のように先ほど作成したデータが表示される。

次に一旦今回のデータを図示して見る。pythonで図示するにはmatplotlibがわかりやすい。
x=df["room_size"]
y=df["tv_inch"]
import matplotlib.pyplot as plt
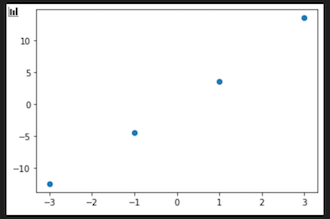
plt.scatter(x,y)
plt.show()
ここでxには部屋の大きさを、yにはテレビのサイズを入れた。
扱いやすそうなデータが取れた。
今回は一次関数で対応できそう(モデルの決定)。
現状このデータをそのまま用いてもいいのだが、このデータをもちいると
y=ax+b
となり、a,bの2つの変数が出てくる。このままでも計算はできるのだが、変数を一つ減らすためにデータの平均化を行う。
データの平均化
全てのデータの平均値を取り、データからそれぞれ引き算した値を用いる。
pandasではデータの平均値をとったり全てのデータに対して引き算することが極めて簡単にできる。
これを行うことでy=axのみを考えることができる。
# データの平均値の取得
xm=x.mean()
ym=y.mean()
# 全てのデータから平均値を引くことで中心化
xc=x-xm
yc=y-ym
# 再表示
plt.scatter(xc,yc)
plt.show()
先ほどのグラフとあまり変化がないようだが切片(b)を考えずに済むので今後の計算がかなり楽になる。
\hat{y}=ax
についてのaを求めればよい。
評価関数の決定
実測値に対して予測値(機械学習を用いたもの)が一番小さくなるように式を決定したい。そのためのものが評価関数の決定という。データサイエンスでいう「損失関数」と意味は同じ。
ここでは説明は少なくするが二乗誤差を確かめて小さいもので決定する。
yを実測値、y^(ワイハット)を予測値として
\begin{align}
L&=(y_1-\hat{y_1})^2+(y_2-\hat{y_2})^2+....+(y_N-\hat{y_1N})^2\\
&=\sum_{n=1}^{N}(y_n-\hat{y_n})^2
\end{align}
で表すことができる。この時Lのことを評価関数という。
評価関数の最小化
評価関数は先ほど見た通り二次関数で現れる。
したがって傾きが0の点が最小となり、二乗誤差が小さい点となる。
高校数学の範囲になるが二次方程式の傾きが0となる点を求めるなら微分を行い「=0」となる点を探せばいい。
変数はaなので
\frac{\partial}{\partial a}(L)=0
を求める。これに先ほどの数式を代入し展開すると
\begin{align}
L&=\sum_{n=1}^{N}y_n^2-2(\sum_{n=1}^{N}x_ny_n)a+(\sum_{n=1}^{N}x_n^2)a^2\\
&=c_o-2c_1a+c_2a^2
\end{align}
代入して
\frac{\partial}{\partial a}(c_o-2c_1a+c_2a^2)=0\\
\\
a=\frac{\sum_{n=1}^{N}x_ny_n}{\sum_{n=1}^{N}x_n^2}
これについてコードを作成して行く。
# 式よりそれぞれの二乗の値を求める
xx=xc*xc
xy=xc*yc
# aを求める
a=xy.sum()/xx.sum()
# プロットしてみる
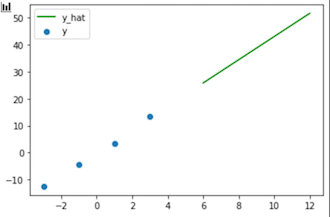
plt.scatter(xc,yc, label="y")
plt.plot(x,a*x, label="y_hat", color="green")
plt.legend()
plt.show()
実測値の範囲でxが定まってるので線分が短くなっているがaを求めれた。
以上により傾きaが求まった。しかし中心化しているので実際に当てはめる際は
x(x値)-x(平均値)をしたものにaをかけて最後にy(平均値)をすることを忘れないこと。
最後にこれをまとめたものを記す。
import pandas as pd
import matplotlib.pyplot as plt
df=pd.read_csv("room_tv.csv")
x=df["room_size"]
y=df["tv_inch"]
# 平均化
xm=x.mean()
ym=y.mean()
# 中心化
xc=x-xm
yc=y-ym
xx=xc*xc
xy=xc*yc
a=xy.sum()/xx.sum()
plt.scatter(xc,yc, label="y")
plt.plot(x,a*x, label="y_hat", color="green")
plt.legend()
plt.show()
おまけ
# データの概要把握
df.describe()
これにより以下のようにデータの解析を行ってくれる。
より複雑で大量なデータの処理の際に役立つ。

最後に
コードとしては短いものであったがとても意味のあるものだった。
次回は重回帰分析を行ってみたいと思います。
今後の展開としてはコーディング、エラー処理などのプログラミング関連だけでなく、神経科学と結びつけたものも投稿していきます。