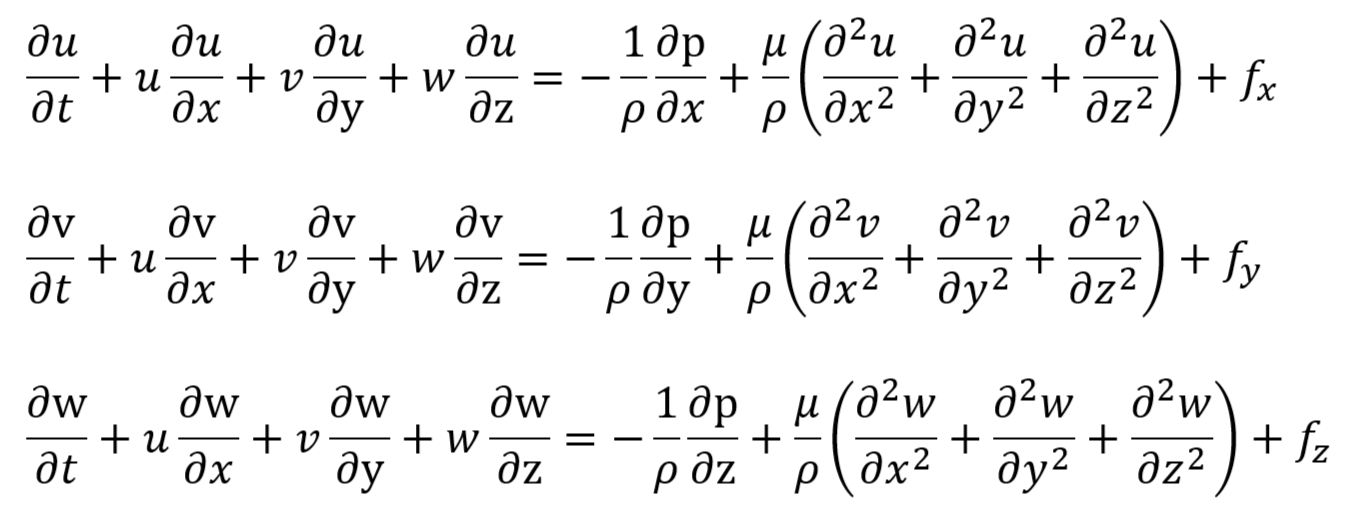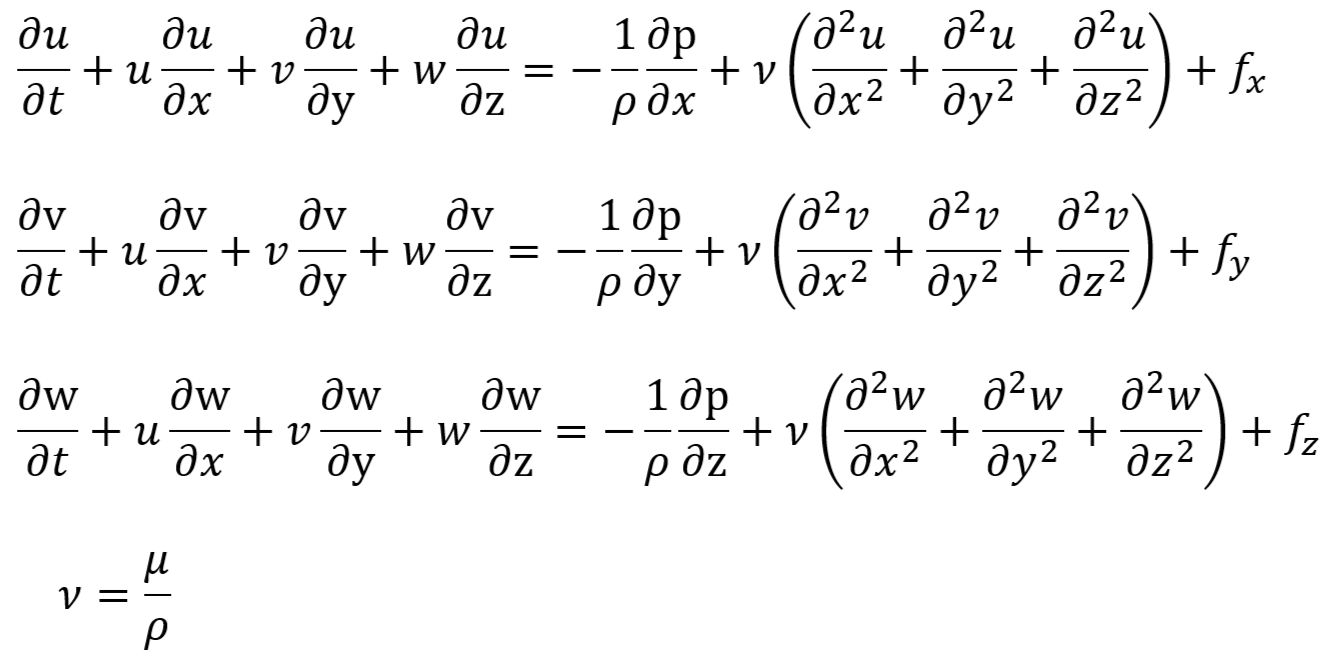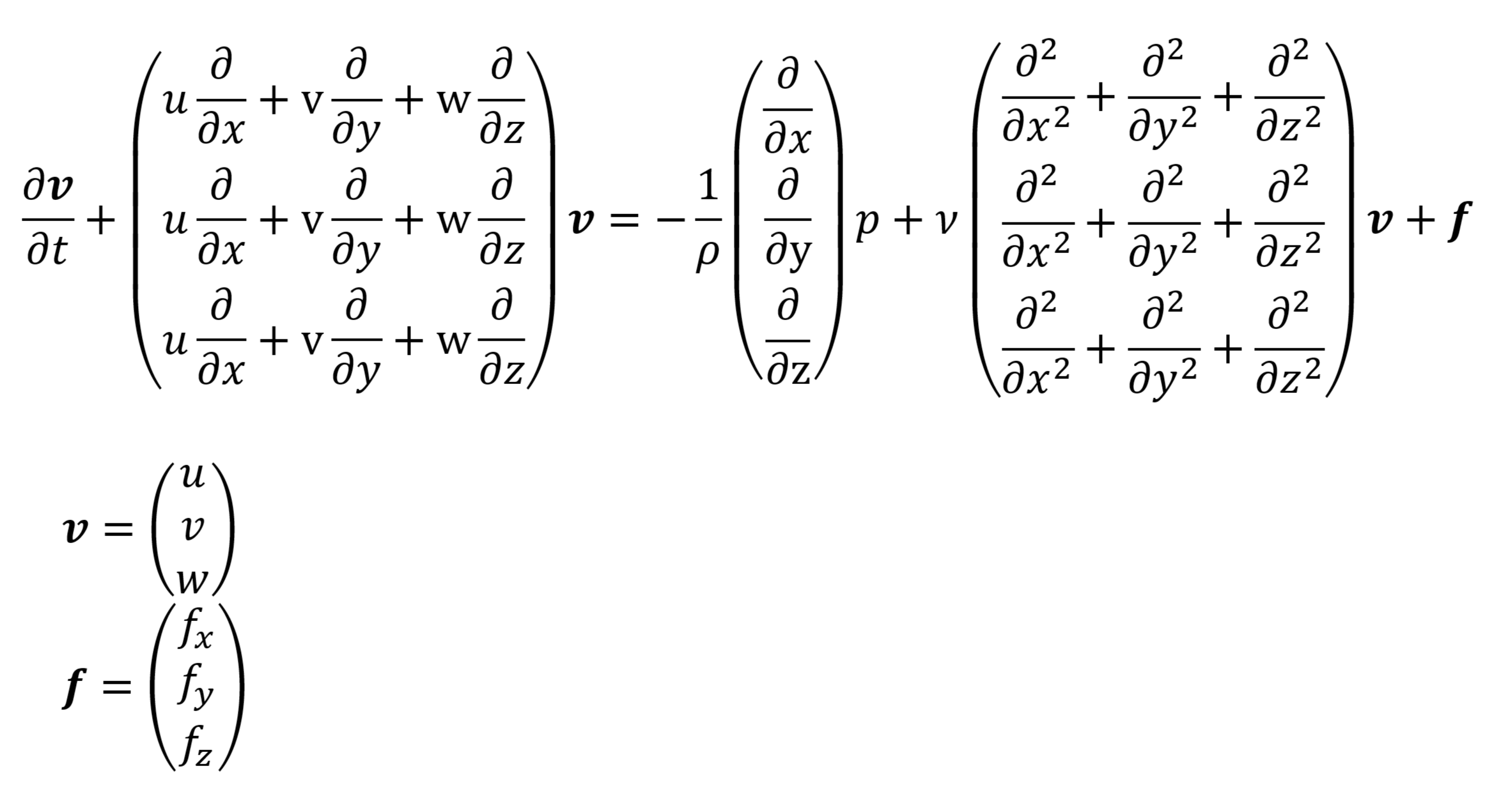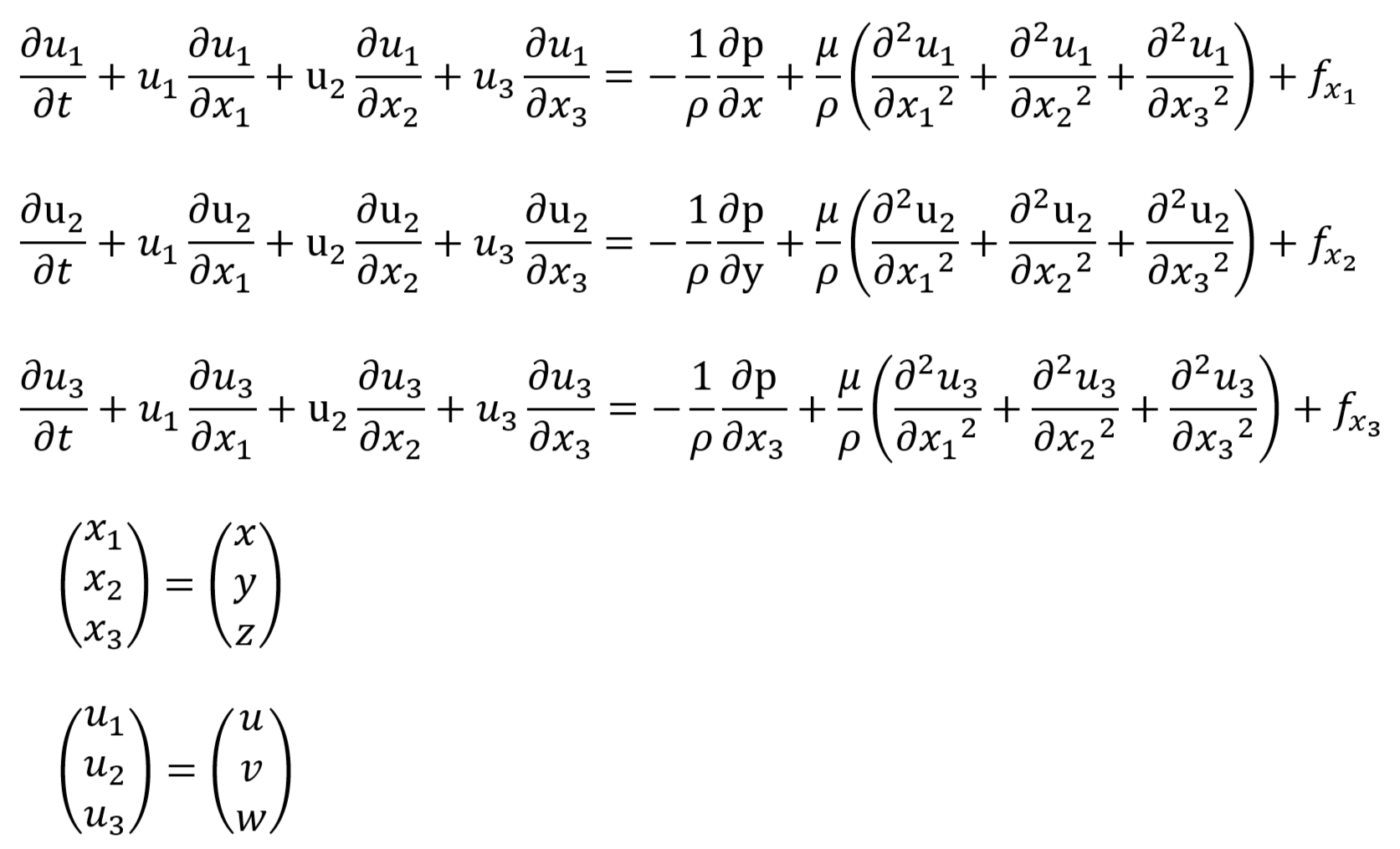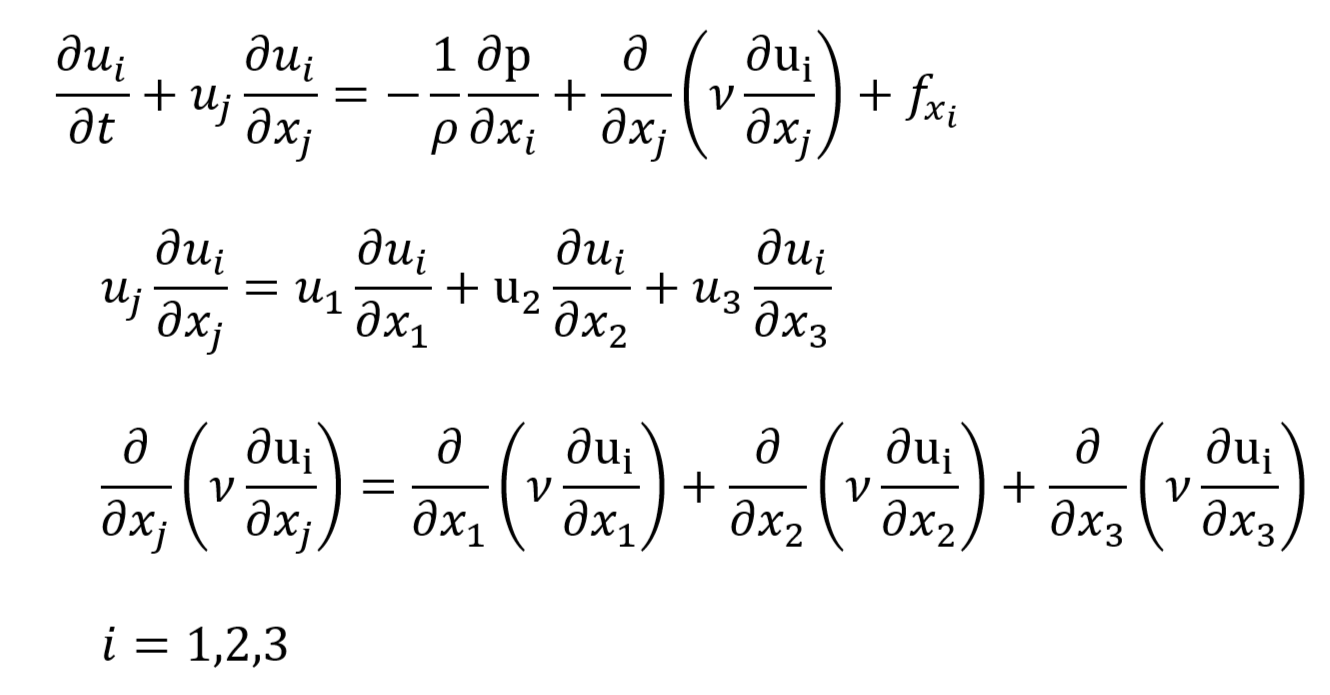流体力学を学ぶ人を悩ませるナビエ・ストークス方程式の表記の違い
取りあえず思いつく限りの非圧縮性流れ(密度一定)かつ粘度一定のNS式をここにまとめておきます。
圧縮性流れや粘度が一定ではない場合は項が増えたり偏微分される変数も増えますが、ナブラ、divとgrad、縮約記法などを用いる表記方法は変わりないと思います。
本取り組みの背景は一番下に記載しています。
注記
-
「/」で区切っている単語は同じ意味でも複数の異なる表現方法があるものです。
-
OneNoteで書いた数式を画像貼り付けしているため数式のサイズがバラバラです。
-
ナブラ、divとgrad、縮約記法などは一つの式の中で混在して用いられる場合があります。
そのような組み合わせまで記述すると膨大な量になるため代表的な記述方法を記載致します。 -
動粘度で表記したり密度を右辺に書く場合なども組み合わせると膨大なパターンになるので代表的な書き方のみ記載しています。
あらかじめご了承ください。
非保存形/convective formのNS式
任意の位置の流体粒子の加速度から導出したNS式を非保存形やconvective formといいます。
① x,y,z方向毎に表した形式
② 動粘性係数/kinematic viscosity/動粘度 νを用いた形式
粘性係数/密度を動粘性係数で置き換えただけ
③ 速度をカッコの外にまとめた形式
④ ベクトル形式
あんまり見たことないが一応載せておく
⑤ ベクトルは太文字で表した場合
⑥ 微分演算子ナブラ∇で表した形式
3つの式が一つの式で表される
よく見かける

⑦ ラプラシアン/ラプラス演算子 Δで表した形式

⑧ 発散div、発散gradで表した形式

∇と組み合わされて使用される場合も多い
⑨ 実質微分/物質微分/ラグランジュ微分を用いた表記

⑩ 空間座標系を下付添え字1,2,3で表した表記
⑪ 縮約記法/総和規約/アインシュタインの縮約記法/アインシュタインノーテーションを用いた表記
⑫ 縮約記法/総和規約/アインシュタインの縮約記法/アインシュタインノーテーションを用いた表記 せん断ひずみの定義に沿って表記した場合
以下のサイト様に記載されていたNS式です。
アインシュタインの総和規約について
右辺第二項を展開して整理し連続の式を用いることで⑪と同じ形式になります。
⑬ 番外編:項の名前
各項に以下のような名前がある。
口頭で話す場合は項の名前で呼び合うが、呼び名は統一されておらず惑わされる。

⑭ 保存形/conservation formのNS式
コントロールボリュームに対する運動量の保存則から導出した形式
CFDソフトウェア内ではこの形式を元に離散化されていることが多い
Nomenclature
x,y,z : 直交座標系の方向
u,v,w : x,y,z方向の速度
p : 圧力
μ : 粘性係数/分子粘性係数
ρ : 密度
fx, fy, fz : 体積力(重力や遠心力)
参考資料
- 数値流体力学第二版 H.K.Versteeg & W. Malalasekera
- Wikipediaのナビエ・ストークス方程式 https://en.wikipedia.org/wiki/Navier%E2%80%93Stokes_equations
- アインシュタインの総和規約について
- その他Googleの画像検索で出てきた様々なNS式の形式を載せてくださっているサイト様
背景
自分が流体力学を学んだとき色々な資料に書いてあるNS式は見た目が全然違っていて同じものと思えませんでした。
そして自分がもとめている式が資料に書いてあるものなのか分からず、そこで資料を読むのを止めてしまいました。
NS式は様々な表記方法があることを知っておけば色々な資料をもうちょっと早く読めたのかと思います。
何かの参考になれば幸いです。
最後に
並べてみて多くの表記方法や表現方法があることに驚きました。
また、Wikipediaにはより一般的な(圧縮性流れや粘度が一定ではない場合)方程式があります。
日本語のWikipediaには速度場の発散にΘを使う方法もありますが、あまり見たことがないので割愛しました。
最後にナビエ・ストークス方程式の原著論文の表記を記載しておきます。
On the Theories of the Internal Friction of Fluids in Motion, and of the Equilibrium and Motion of Elastic Solids
https://archive.org/details/cbarchive_39179_onthetheoriesoftheinternalfric1849/page/n1/mode/2up?view=theater

現代とほとんど記述の仕方は変わっていませんね。
特徴としては全部左辺に持っていってます。
密度は一定扱いなので非圧縮流れになり第二粘性項は連続の式からゼロとなりますが
この項については私が良く理解していないので間違っているかも知れません。
多分、人の数だけ表現方法が異なる方程式かと思います。
自分なりに納得しやすい表記方法が見つかれば良いかと思います。