はじめに
今回は、「ChatGPTにハンズオンを作らせてみた」の第5弾で、操作変数法を勉強しました。
第4弾はこちら↓
操作変数法
「説明変数($X$)には影響を与えるが、目的変数($Y$)には直接影響しない」ような操作変数($Z$)を使って$X$を推定し、その推定値を用いて$Y$を回帰することで、$X$の真の因果効果を求めるための手法。回帰分析の応用手法でありながら、因果推論の文脈でも用いられる。
使用データ
scikit-learnのデータセットの1つである、カリフォルニアの住宅価格データを使用しました。その中でも、今回は次の3つの変数をピックアップして使用しました。
| 変数 | 説明 |
|---|---|
| MedHouseVal | 住宅価格(目的変数) |
| AveRooms | 平均部屋数(説明変数) |
| MedInc | 世帯の平均年収(交絡因子) |
| Population | 人口密度(操作変数) |
- 目的変数:説明変数の影響を受ける変数
- 説明変数:目的変数を説明するための変数
- 交絡因子:説明変数と目的変数の両方に影響を与える変数(操作変数法の計算では使わない)
- 操作変数:説明変数には影響を与えるが、目的変数には直接影響しない変数
やること
- 目的変数($Y$)と説明変数($X$)を用いて、通常の回帰分析を実装
- 操作変数($Z$)を使って、説明変数($X$)を推定する回帰分析を実装
- 2.で得られた推定値($\hat{X}$)を使い、目的変数($Y$)に対する回帰を実装
- 1.で得た回帰係数と3.で得た回帰係数を比較して、因果関係を考察
使用コード・分析結果
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
from linearmodels.iv import IV2SLS
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
# データの取得
california = fetch_california_housing(as_frame=True)
df = california.frame
目的変数(MedHouseVal)と説明変数(AveRooms)を用いて、通常の回帰分析を実装します。
# OLS回帰 (部屋数 -> 住宅価格)
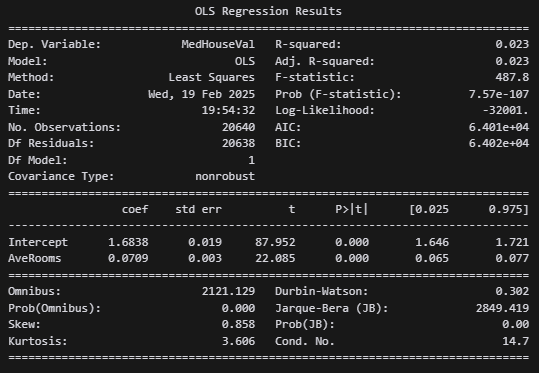
ols_model = smf.ols("MedHouseVal ~ AveRooms", data=df).fit()
print(ols_model.summary())
-
AveRoomsの回帰係数0.0709より、「平均部屋数が1部屋増えると、住宅価格が0.0709(約7.1%)上昇する」ことを意味する。 - p値が0.000(有意水準1%以下)であるため、
AveRoomsの影響は統計的に有意と判断できる。 - 95%信頼区間は、
[0.065, 0.077]であり、効果が正であることを示唆している。 -
R²=0.023より、AveRoomsだけでは住宅価格の変動の 約2.3% しか説明できない。 - モデル全体の説明力が低いため、交絡因子(
MedIncなど)の影響が強いと考えられる。
操作変数(Population)を用いて、説明変数(AveRooms)の予測値を得ます。
first_stage = smf.ols("AveRooms ~ Population", data=df).fit()
df["AveRooms_hat"] = first_stage.predict(df["Population"])
先ほど得た予測値(AveRooms_hat)と目的変数(MedHouseVal)を用いて、回帰分析を実装します。
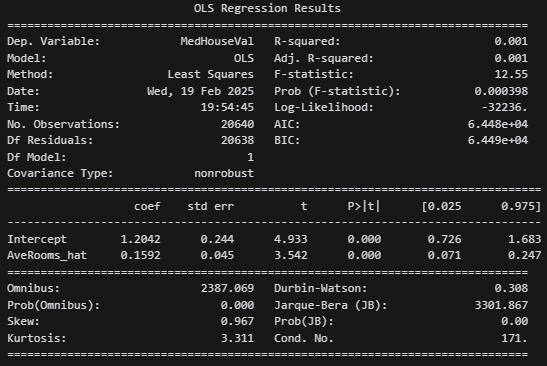
second_stage = smf.ols("MedHouseVal ~ AveRooms_hat", data=df).fit()
print(second_stage.summary())
-
AveRooms_hatの回帰係数0.1592より、「平均部屋数が1部屋増えると、住宅価格が0.1592上昇する」と推定されたことを意味する。 - p値が0.000(有意水準1%以下)であるため、
AveRooms_hatの影響は統計的に有意と判断できる。 - 95%信頼区間は、
[0.071, 0.247]であり、効果が正であることを示唆している。
print(f"OLSの回帰係数 (AveRooms -> MedHouseVal): {ols_model.params['AveRooms']}")
print(f"IVの回帰係数 (AveRooms -> MedHouseVal): {iv_model.params['AveRooms']}")
OLSの回帰係数 (AveRooms -> MedHouseVal): 0.07086879328040531
IVの回帰係数 (AveRooms -> MedHouseVal): 0.15920474604229184
- OLS(通常の回帰分析)の係数と比べて、IV(操作変数法)の係数が約2.2倍の値になっている。
- OLSで過小評価されていた
AveRoomsの因果効果が、操作変数法によって、正しく推定された可能性がある。 - ただ、ともに決定係数の値が小さいため、住宅価格を決める要因としては
AveRoomsは
おわりに
今回の操作変数法は、これまでの因果推論の手法とは考え方が少し違ったので、理論の理解が難しかったです。