Kaggleの「Student Performance Data Set」で回帰不連続デザインを実装してみた

はじめに

今回は、「ChatGPTにハンズオンを作らせてみた」の第2弾で、回帰不連続デザイン（RDD）を勉強しました。

第1弾はこちら↓

回帰不連続デザイン（RDD）

特定の閾値（カットオフ）を基準に、処置（介入）を受けたグループと受けていないグループを比較する手法。因果推論の一種であり、政策評価やマーケティングなどの分野で使われる。

使用データ

Kaggleのデータセットにある、「Student Performance Data Set」というポルトガルの中学生の学業成績と、それに関するさまざまな要因をまとめたデータセットを用いました。その中でも、今回は次の2つの変数をピックアップして使用しました。

指標	説明	備考
Dalc	平日のアルコール摂取量	1:ほとんど飲まない 2:少し飲む 3:普通 4:よく飲む 5:非常に多く飲む
G3	最終学年での成績評価	0-20の間の数値

使用コード・分析結果

# 必要なライブラリのインポート
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.linear_model import LinearRegression

# データの読み込み
df = pd.read_csv('student-por.csv')

# 'Dalc' の分布
plt.hist(df['Dalc'], bins=5, edgecolor='k')
plt.xlabel('Dalc (平日のアルコール摂取量)')
plt.ylabel('学生数')
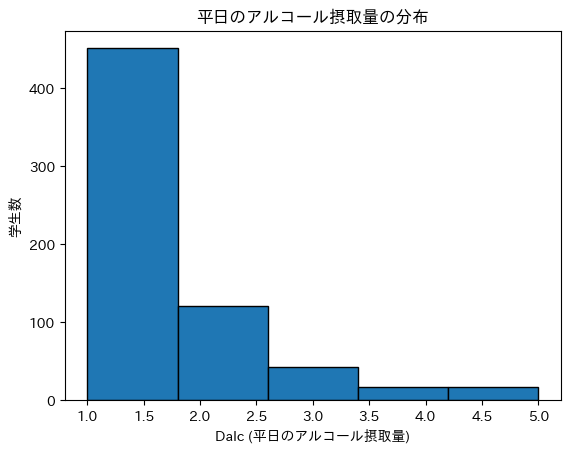
plt.title('平日のアルコール摂取量の分布')
plt.show()

# 'G3' の分布
plt.hist(df['G3'], bins=20, edgecolor='k')
plt.xlabel('G3 (最終成績)')
plt.ylabel('学生数')
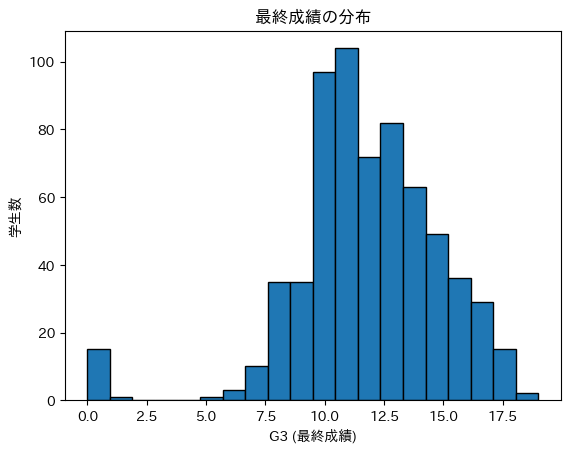
plt.title('最終成績の分布')
plt.show()

• 特徴
  • Dalc = 1 の学生が圧倒的に多く、アルコール摂取量が増えるほど人数が減少。
  • Dalc >= 3 の学生の割合は非常に少ない。
• RDD適用への影響
  • カットオフ（Dalc=3）を境に分析する際、高摂取群のデータ数が非常に少なくなるため、結果のばらつきが大きくなる可能性がある。
  • 分析の精度を上げるには、カットオフをDalc=2に変更するか、異なるデータセットを用いる必要があるかもしれない。

• 特徴
  • G3の分布はほぼ正規分布に近い形をしている。
  • 成績が10-15の範囲に集中している。
  • G3 = 0の学生が少数いる → これらは単位不認定やデータの異常値の可能性がある。
• RDD適用への影響
  • Dalcによる影響を分析する際、成績の変動が適度に分布しているため、回帰分析には適している。
  • ただし、極端な低成績者（G3=0）がいるため、これらのデータを取り除くか、別途考慮するのが望ましい。

いったんそのまま分析してみた

# カットオフ値
cutoff = 3

# カットオフ前後のデータを分割
df_low = df[df['Dalc'] < cutoff]
df_high = df[df['Dalc'] >= cutoff]

# 説明変数と目的変数の設定
X_low = df_low[['Dalc']]
y_low = df_low['G3']
X_high = df_high[['Dalc']]
y_high = df_high['G3']

# 線形回帰モデルの作成
model_low = LinearRegression().fit(X_low, y_low)
model_high = LinearRegression().fit(X_high, y_high)

# 回帰直線の傾きと切片の表示
print(f"低摂取群の回帰直線: y = {model_low.coef_[0]:.2f}x + {model_low.intercept_:.2f}")
print(f"高摂取群の回帰直線: y = {model_high.coef_[0]:.2f}x + {model_high.intercept_:.2f}")

# 散布図の作成
plt.scatter(df['Dalc'], df['G3'], alpha=0.5, label='データポイント')

# 回帰直線の描画
Dalc_range = np.linspace(df['Dalc'].min(), df['Dalc'].max(), 100).reshape(-1, 1)
plt.plot(Dalc_range, model_low.predict(Dalc_range), color='blue', label='低摂取群の回帰直線')
plt.plot(Dalc_range, model_high.predict(Dalc_range), color='red', label='高摂取群の回帰直線')

# カットオフラインの描画
plt.axvline(x=cutoff, color='black', linestyle='--', label='カットオフ (Dalc=3)')

# グラフの装飾
plt.xlabel('Dalc (平日のアルコール摂取量)')
plt.ylabel('G3 (最終成績)')
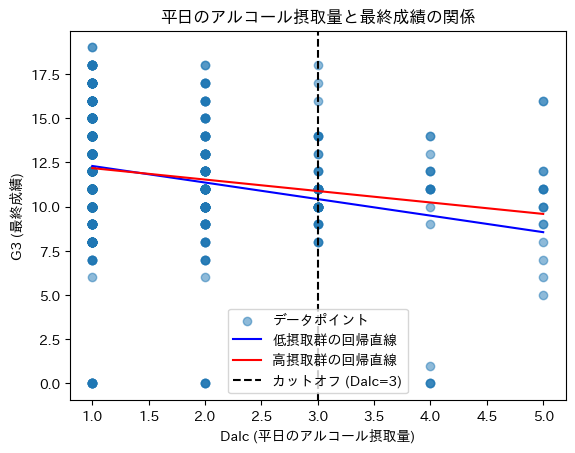
plt.title('平日のアルコール摂取量と最終成績の関係')
plt.legend()

カットオフ（Dalc=3)を境に成績が不連続に変化しているか？

• 低摂取群（Dalc<3）と高摂取群（Dalc>=2）の回帰直線を比較すると、わずかに傾きの違いが見られる
• しかし、明確な不連続（ジャンプ）は見られないため、Dalc=3の影響は限定的である可能性がある。
• 成績の変化が小さいため、因果関係の特定は難しい。

Dalc=1+Dalc2 = 451+121 = 572
Dalc=3+Dalc=4+Dalc=5 = 43+17+17 = 77
→さすがに差が大きすぎるので、カットオフの基準をDalc=3からDalc=2に変えてみる。

境をDalc=2に変えてみた

# カットオフ値
cutoff = 2

# カットオフ前後のデータを分割
df_low = df[df['Dalc'] < cutoff]
df_high = df[df['Dalc'] >= cutoff]

# 説明変数と目的変数の設定
X_low = df_low[['Dalc']]
y_low = df_low['G3']
X_high = df_high[['Dalc']]
y_high = df_high['G3']

# 線形回帰モデルの作成
model_low = LinearRegression().fit(X_low, y_low)
model_high = LinearRegression().fit(X_high, y_high)

# 回帰直線の傾きと切片の表示
print(f"低摂取群の回帰直線: y = {model_low.coef_[0]:.2f}x + {model_low.intercept_:.2f}")
print(f"高摂取群の回帰直線: y = {model_high.coef_[0]:.2f}x + {model_high.intercept_:.2f}")

# 散布図の作成
plt.scatter(df['Dalc'], df['G3'], alpha=0.5, label='データポイント')

# 回帰直線の描画
Dalc_range = np.linspace(df['Dalc'].min(), df['Dalc'].max(), 100).reshape(-1, 1)
plt.plot(Dalc_range, model_low.predict(Dalc_range), color='blue', label='低摂取群の回帰直線')
plt.plot(Dalc_range, model_high.predict(Dalc_range), color='red', label='高摂取群の回帰直線')

# カットオフラインの描画
plt.axvline(x=cutoff, color='black', linestyle='--', label='カットオフ (Dalc=3)')

# グラフの装飾
plt.xlabel('Dalc (平日のアルコール摂取量)')
plt.ylabel('G3 (最終成績)')
plt.title('平日のアルコール摂取量と最終成績の関係')
plt.legend()

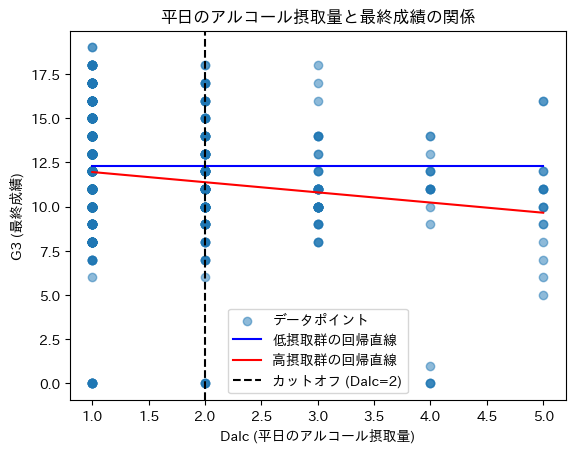
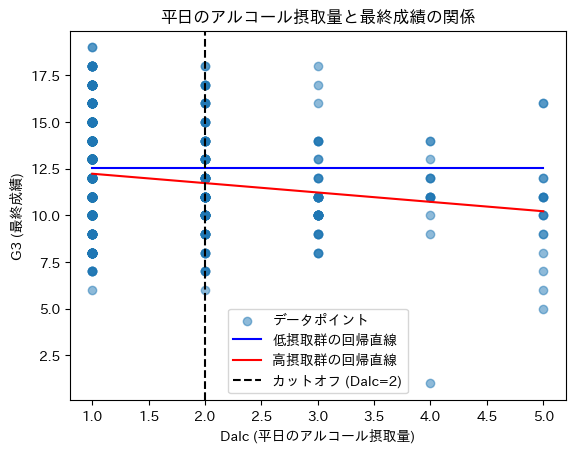
カットオフ（Dalc=2)を境に成績が不連続に変化しているか？

• 低摂取群（青線）はほぼ水平で、アルコール摂取量の影響があまり見られず、成績は一定のまま。
• 高摂取群（赤線）は、Dalcが増えるほど成績が低下する傾向が強まっている。

Dalc=1 = 451
Dalc2+Dalc=3+Dalc=4+Dalc=5 = 121+43+17+17 = 198
→まだ差はすごいけど、一応結果は出た
→念のため、G3=0を除いて、Dalc=2でカットオフしてみる

G3=0を除いて、Dalc=2でカットオフしてみた

df_filtered = df[df['G3'] != 0]

# カットオフ値
cutoff = 2

# カットオフ前後のデータを分割
df_low = df_filtered[df_filtered['Dalc'] < cutoff]
df_high = df_filtered[df_filtered['Dalc'] >= cutoff]

# 説明変数と目的変数の設定
X_low = df_low[['Dalc']]
y_low = df_low['G3']
X_high = df_high[['Dalc']]
y_high = df_high['G3']

# 線形回帰モデルの作成
model_low = LinearRegression().fit(X_low, y_low)
model_high = LinearRegression().fit(X_high, y_high)

# 回帰直線の傾きと切片の表示
print(f"低摂取群の回帰直線: y = {model_low.coef_[0]:.2f}x + {model_low.intercept_:.2f}")
print(f"高摂取群の回帰直線: y = {model_high.coef_[0]:.2f}x + {model_high.intercept_:.2f}")

# 散布図の作成
plt.scatter(df['Dalc'], df['G3'], alpha=0.5, label='データポイント')

# 回帰直線の描画
Dalc_range = np.linspace(df['Dalc'].min(), df['Dalc'].max(), 100).reshape(-1, 1)
plt.plot(Dalc_range, model_low.predict(Dalc_range), color='blue', label='低摂取群の回帰直線')
plt.plot(Dalc_range, model_high.predict(Dalc_range), color='red', label='高摂取群の回帰直線')

# カットオフラインの描画
plt.axvline(x=cutoff, color='black', linestyle='--', label='カットオフ (Dalc=2)')

# グラフの装飾
plt.xlabel('Dalc (平日のアルコール摂取量)')
plt.ylabel('G3 (最終成績)')
plt.title('平日のアルコール摂取量と最終成績の関係')
plt.legend()

• G3=0を除く前と比べて、大きな変化は見られなかった。

Dalc=1 = 443
Dalc2+Dalc=3+Dalc=4+Dalc=5 = 117+43+17+14 = 191
→G3=0は、「アルコールを摂取しすぎて、単位認定されなかった」という人（Dalc>=3ぐらい）が多いのかなと勝手に推測していたが、意外とそうでもなかった。
→Dalc=1は11、Dalc>=2は7で、両クラスが同数に近い形で減ったので、特に大きな変化はなかった。

おわりに

本来は、既にある仮設の検証をするうえで、分析途中にカットオフの基準を変えていくのは不適切な気がしますが、今回は練習なので目をつぶっておきます。