1978年発行という古い本。入門の名にふさわしく、基礎から順序だてて体系的に説明しており、高校数学程度の前提知識だけで理解できる。大部分が基本的な数学と力学の説明で、有限要素法自体の内容は少ない。最後に第二部として応用的な内容が紹介されているが詳細な説明はなく、次のステップへの道しるべのようになっている。
論理は明解で、混乱を招くような定義漏れや誤字脱字などもなく整っており、自分のような初学者も安心して読める。素晴らしい良書だった!古くから読み継がれている本というのは洗練されている。
構成
最初の1/3は基本的な線形代数のみ。大学数学でやるような抽象的なベクトルの定義からのスタートではなく、数のセットとしてベクトルを定義するやり方。分かりやすさに重点を置いている。
線形代数の後は複数のバネからなる系を表す剛性マトリクスの説明。一見 有限要素法と関係ない話のように見えるのだが、実は有限要素法はこの理論から発祥したものらしい。そのことが後になって分かる。
剛体マトリクスの次は弾性体力学の解説。基本的なことから明解に解説しており、弾性体力学を学んだことがない自分でもすんなりと理解することが出来た。
ここまでが本書の半分を占めるのだが、有限要素法の説明はまだ始まらない。この本では有限要素法を理解するための前提知識の解説に多くの紙面を費やしている。有限要素法の理論自体はとても単純なので、このやり方はとても良いと思う。
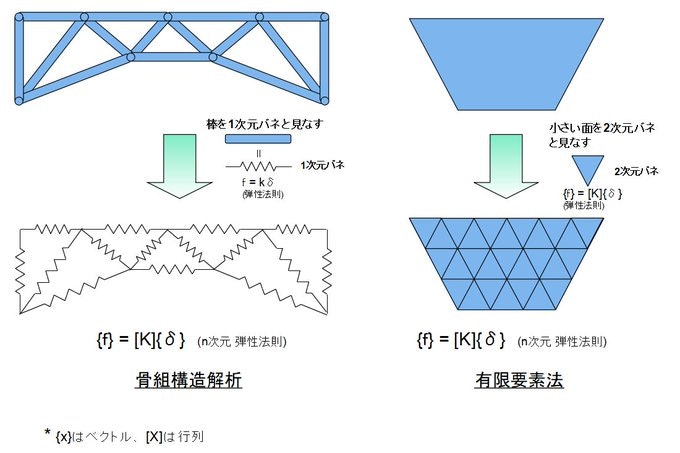
次でようやく有限要素法の開始。かと思いきや、剛性マトリクスを利用した骨組構造解析の手法の解説が始まる。棒からなる構造物を考えるとき、棒を一つのバネ要素とみなし、バネ要素一つ一つに剛性マトリクスを求め、それらを合成した行列を作る。その行列からなる連立方程式を解くことで力やひずみの解析が出来る。
その後 本当に有限要素法が始まる。有限要素法は骨組構造解析を一般化しただけのもの。計算のやり方は全く同じ。結局のところ、有限要素法としての説明は、紙面上はわずか15ページほどにしか過ぎない。拍子抜けするほど簡単で、入門としてはとても分かりやすい。
このあとは第II部 応用編となっており、説明は大雑把で結論しか載ってない。詳細説明は他の書籍に譲るといったところか。Fotranによる具体的な解析例も記載されているが、今となってはいささか古いので参考として読み流してもいいと思う。自分の好きな言語で実装してみると良い勉強になる。
本書の特徴
もともと有限要素法はこのように骨組み構造解析から生まれたものだそうである。しかしこれを一般の物理現象を表す微分方程式を解く手法として一般化することが出来る。初めから一般化して数学的に有限要素法を説明している本もあるようだが、この本では歴史的な道筋の通りに説明している。最初から抽象的な説明を受け入れるのはなかなか難しい。初心者にとっては、たとえ特殊な一つの例にすぎなかったとしても、具体的なものから導入して説明された方がずっと分かりやすい。
この本を読んだことで有限要素法の全てが分かるわけではないが、入門書としては間違いなく良書であると思う。
C#で実装してみた
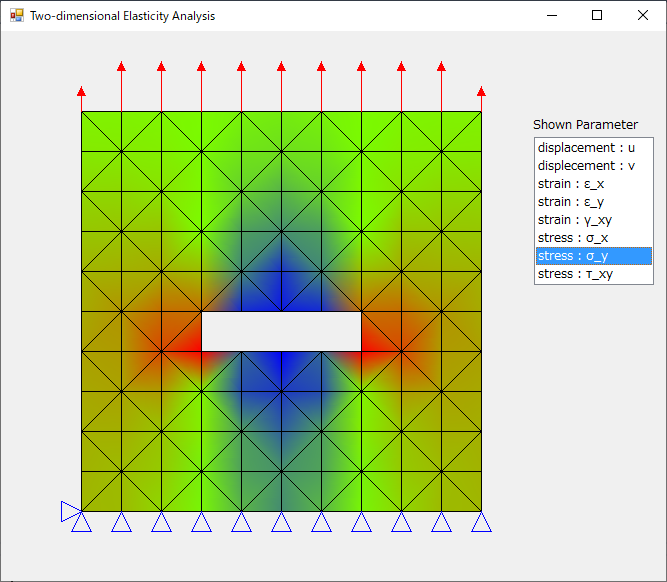
それっぽい変位・ひずみ・応力の分布が得られた。やっていることは単に小さい三角形ごとに行列を作って、それらを重ね合わせた行列がなす連立方程式を解いているだけ。こんなシンプルなプログラムでこんな凄いことが出来る。結果が出ると楽しいし、数値計算や画像表示のプログラミングのいい練習にもなる。
ここでは規則正しく並んだ要素からなる正方形という簡単な形状を解析対象としているが、これは単に入力の形状データを作る作業を楽にしたかったためである。有限要素法の凄いところはどんな複雑な形状をしていようと全く同じ方法で計算出来るところである。自分で適当に節点を設定して細かい三角形に分割してその座標を入力するだけで、どんな問題も同じように解ける。
任意形状に対する分割データの作成作業自体もプログラム化することは出来るが有限要素法の本質と関係ないので今回は実装しなかった。それはまた別の機会に考えよう。
コードはGitHubに置いた。WindowsFormsApp2/WindowsFormsApp2/Form1.csがメインのコード。
https://github.com/MhageGH/FEM-exmaple