2次元 Wavelet 行列を用いた定数時間メディアンフィルタ日本語解説（SIGGRAPH Asia 2022 Best Paper）

初めましての方は初めまして。私は東京大学大学院 情報理工学系研究科で博士2年生をしている学生です。

"Constant Time Median Filter using 2D Wavelet Matrix"、日本語に直すと「ウェーブレット行列を用いた定数時間メディアンフィルタ」と言う論文を書き、ACM SIGGRAPH が開催するグラフィックス分野のトップカンファレンス SIGGRAPH Asia 2022 の Technical Papers へ採択され、更にこの中から選ばれる Best Paper Award をいただきました。🎉

今回はこの論文の簡単な日本語解説と、論文では書かれていないちょっとした裏話などをしていきたいと思います。

• プロジェクトページ
• SIGGRAPH Asia のプレゼン概要ページ
• ACM DIGIRAL LIBRARY
• GitHub のコード

良ければこの Qiita 記事のいいね・ストック、GitHub の Star をしていただけると今後のモチベーションに繋がります。
また、ACM DIGIRAL LIBRARY から論文 PDF をダウンロードしていただけると、DLカウンタが増えて嬉しいです。

また、SIGGRAPH Asia での発表の際に用意した 18分のプレゼン映像も公開しています。良ければ高評価・チャンネル登録よろしくお願いします。

なにをしたの？(Abstract)

• メディアンフィルタと言う、様々な処理に用いられている古典画像フィルタの高速化をした

• これまでソート法かヒストグラム法の2手法があったが、全く新たな第三の手法を提案

• 競プロでよく用いられているウェーブレット行列(Wavelet Matrix)をベースに、画像処理に使えるように拡張した

• 既存2手法でどちらも不得意だった、「HDR(高色ビット)」や「中～巨大フィルタサイズ」でも効率的に扱える

• 並列化もサポートし、GPU (CUDA) で既存手法と比較し 10～100 倍の高速化を達成

• ACM SIGGRAPH の開催する コンピュータグラフィックスのトップカンファ SIGGRAPH Asia 2022 のテクニカルペーパーに採択。Best Paper Award を受賞

こちらのツイートでも簡単に研究の概要・貢献を紹介しています。

◆報告◆
CG分野最高峰の ACM SIGGRAPH Asia（テクニカルペーパーJournal）に論文が採択されました！

競プロでおなじみ【Wavelet Matrix】を2次元整数列に拡張、従来O(WHr^2log r)かO(WH2^b)かかっていたメディアンフィルタをO(WHb logW)に落とし

更に並列化にも対応してGPUで圧倒的高速化しました！ pic.twitter.com/5oFJGJbpAo

— 百千万億 萬◆つもいよろず (@TumoiYorozu) August 4, 2022

目次(Outline)

以下の順序で紹介していきます。1～5章は論文の内容を日本語で解説・一部補足などを行っています。
6～8章は今回の研究にまつわる背景や考察を行っています。
2.ウェーブレット行列の話や 3.提案手法 の話は、アルゴリズムや競技プログラミングのバックグラウンドが無いと読むのが大変かもしれません。辛いなと思ったら斜め読みして雰囲気だけでもつかんでいただけたらと思います。

• 1. 研究の背景と、既存の手法
  メディアンフィルタについての紹介をします。
• 2. ウェーブレット行列
  アイディアのベースとなったウェーブレット行列の説明です。
• 3. 提案手法
  ウェーブレット行列を拡張して、2次元整数配列（＝画像）を扱えるようにします。
• 4. 評価(Result)
  実際の速度の結果や、メモリ使用量の説明をします。
• 5. 制約と今後の課題
  Limitation & Future Work です。
• 6. この研究の経緯
  この研究のアイディアのきっかけなどを紹介します。
• 7. 査読の感触
  査読で査読者からの評価や突っ込まれた所を紹介します。
• 8. Best Pepar Award をいただけた事の分析
  自己分析をしています。
• 9. まとめ

1. 研究の背景と、既存の手法

メディアンフィルタとは？

数ある画像処理フィルターの一つに、メディアンフィルタ（中央値フィルタ）という物があります。
これはモノクロ画像のあるピクセルに対して、上下左右 $r$ ピクセルの領域の中の中央値の値を採用していくフィルタです。RGB などのカラー画像に関しては色チャンネル毎に処理します。

1974 年に考案された非常に古典的なフィルタであり、画像処理の教科書にも載っている定番のフィルタです。画像処理の定番ライブラリである OpenCV にも medianBlur として実装されていますし、Intel による画像処理ライブラリ Intel IPP にも FilterMedian として実装されています。また Photoshop の「中央値（メディアン）フィルター」、GIMP の「メディアンぼかし」、Premiere Pro や After Effects の「ミディアン」など、各種画像・動画編集ソフトでも標準的に実装されています。

工学的にはノイズ除去フィルタとして使われたり、ぼかしフィルタの一つとしても使われています。

また、映像制作をする人の間では、文字やロゴなどの簡単にできる溶解表現としても使われてもいます。

他にも、美肌化フィルタの一部工程など、様々な用途の構成要素として、メディアンフィルタやその派生が使われています。

主なメディアンフィルタの実装

これまでのメディアンフィルタの主な実装方法としては、主に以下の2通りがありました。

• ソートベースの手法
• ヒストグラムベースの手法

ソートベースの手法

ソートベースの手法では、ピクセルの対象範囲をソートして順番に並べることにより中央値を求めます。シンプルな手法ですが特に $3 \times 3$ といった小さなフィルタのときは最速の手法です。しかしフィルタの半径を大きくしようとした場合、フィルタの1辺サイズを$n$ としたとき、$n^2$ 個の要素をソートしないといけなくなります。単純にソートした場合は1ピクセルあたり $O(n^2 \log n)$ の時間がかかってしまいます。
中央値を求めるのに全てソートする必要は無いと言う発想で、クイックセレクトと言うアルゴリズムを使うことで平均 $O(n^2)$ で、median of medians というアルゴリズムで最悪計算量も $O(n^2)$ にすることが出来ますが、どちらにしろフィルタサイズが大きくなると非常に遅くなってしまいます。
また、最近のソートベースの手法は ソーティングネットワークと呼ばれる、2つの値をmin/maxを用いて交換することでソートする手法がメジャーです．クイックソートなどと違って if を使わず、min/max 命令でどんな値が来ても同様の手順でソートができるので、特に GPU などの条件分岐に弱いアーキテクチャでも相性が良いのですが、多数の値を効率よくソートできるソーティングネットワークというものは未解決問題です。また、単純には $O(n^2 (\log n)^2)$ の計算量がかかってしまいます。隣り合うピクセル同士で処理を共通化することにより計算量を下げることは出来ますが、やはりフィルタサイズの上昇には弱い手法となっています。

ヒストグラムベースの手法

8bit画像の場合、各ピクセルの値域は0～255になります。あるフィルタ区間でそれぞれの値が何回登場したかをカウントする配列（ヒグトグラム）を用意すると、隣のピクセルの計算をするときにヒストグラムを再利用して、差分のピクセルの値だけカウントを更新することで、（ヒストグラムを操作するのに 256 回のメモリアクセスが必要になりますが）フィルタサイズに関わらずに中央値を計算することができます。これだけでも、ピクセルあたり計算量 $O(n)$ のメディアンフィルタが実現可能です。
更に、列ごとに連続 n マスのヒストグラムを用意し、行ごとに n 個の列ヒストグラムを加減算することで、ピクセルあたり $O(1)$ の時間、つまり定数時間のメディアンフィルタが実現できます。OpenCV の メディアンフィルタはこの方式が採用されています。
しかし、定数時間でフィルタリングできるとは言え、$n$ に対して定数というだけであり、ピクセル値のビット数 $b$ に対しては $O(2^b)$ の時間がかかります。近年、High Dynamic Range (HDR) 画像という、16 bit int や 32bit float といった高ビットの色空間で作業することも多く、それらの画像でメディアンフィルタを行う場合はこのヒストグラム法では現実的ではありません。実際、OpenCV のメディアンフィルタは、16, 32bit 画像（かつフィルタサイズが一定以上）の場合はサポートされていません。

既存手法のまとめと、ウェーブレット行列を使った第三の手法（提案手法）

これらの特性から、主にフィルタ半径が小さい場合はソート法、色ビット数が小さい場合はヒストグラム法が用いられてきました。
しかし、古くから利用され研究されてきたメディアンフィルタですが、フィルタ半径が大きい かつ HDR画像 の場合は、どちらの手法も適さないものでした。

ここで、提案手法では、HDRに対応しつつ、フィルタ半径に影響されない、ウェーブレット行列を用いた全く新たな第三の手法 を提案しました。

	ソート法	ヒストグラム法	提案手法
計算量	約$O(r^2)$ 🔺	$O(1)$ ✅	$O(1)$ ✅
HDR	Yes ✅	No ❌	Yes ✅

2. ウェーブレット行列

ウェーブレット行列とは、長さ $n$ の 1次元の $b$ bit 整数配列に対して、$O(nb)$ の時間の前処理を行うことで以下のような区間クエリを求められるデータ構造です。

• Quantile(L, R, k) : 配列の区間 $[L, R)$ の中で、$k$ 番目に小さい値を答える
• RangeFreq(L, R, x, y) : 配列の区間 $[L, R)$ の中で、値域が $[x, y)$ の要素数を答える

単純に考えると、どちらの操作も計算量は $O(R-L)$ になりそうですが、ウェーブレット行列はこれらのクエリを、区間の長さや中身、答えにかかわらず $O(b)$ の時間で答えることができます。
更に、メモリ使用量に関しても十分省メモリに実装することができ、真面目に実装すると $nb + o(nb)$ [bit] のスペース、つまりもともとの数列を表すのに必要な $nb$ bit 分と、$o(nb)$ bit の領域しか使用しません。

ウェーブレット行列とは、ウェーブレット木というものを、答えられるクエリや計算量はそのままに、効率化したものです。ウェーブレット行列を知るためにはウェーブレット木から学習することをおすすめします。以下の記事がおすすめです。

• ウェーブレット木の世界

（一応、この知識がなくても分かるようには説明を構成していますが、知っておいたほうが理解の助けになるでしょう）

なお、画像処理分野でよく用いられるウェーブレット変換とは、直接的な関係はありません。
ウェーブレット行列はこれらの特性から、データベース検索やDNA解析、競技プログラミングの世界で有名なデータ構造でした。
次に、ウェーブレット行列の作り方を、例とともに簡単に紹介します。

構築

ウェーブレット行列は、クエリに答える前に構築を行います。

構築では、各値を2進数で考えていき、上のビットから 0/1 で安定ソートを行っていきます。手順としては基数ソート と似ています。違うのは、基数ソートでは下のビットから注目していきますが、ウェーブレット行列の構築では上のビットから注目していきます。

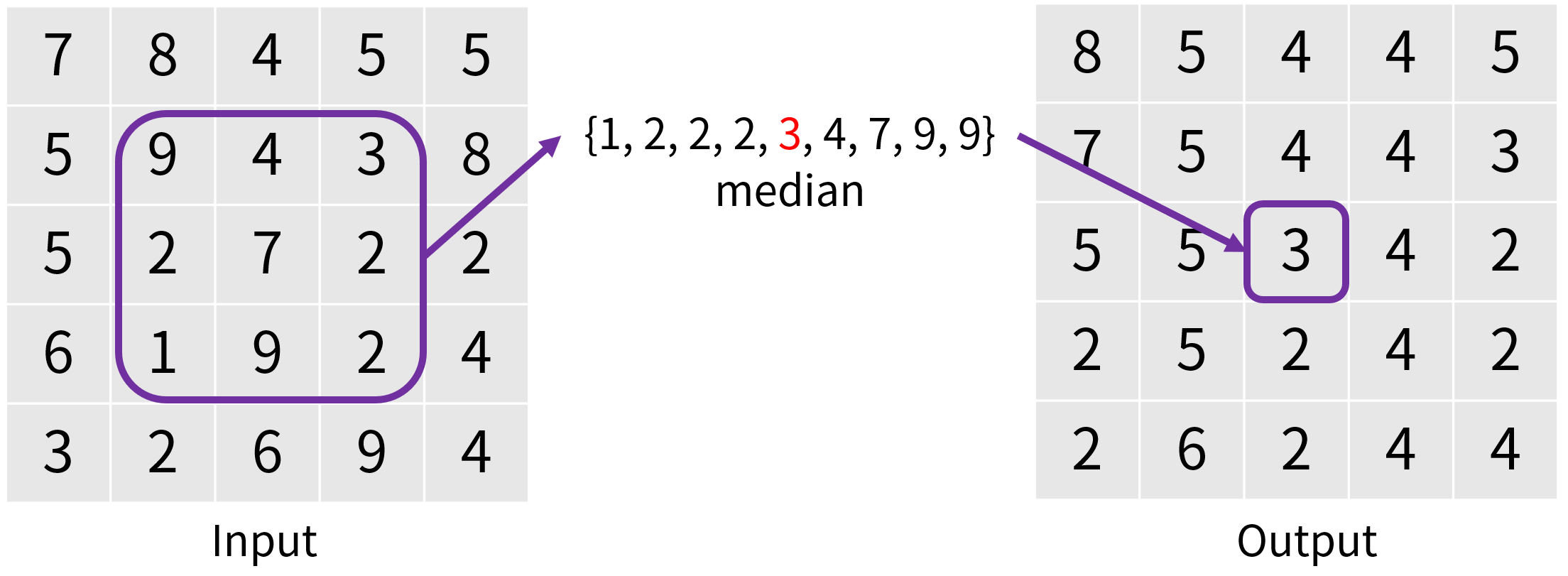
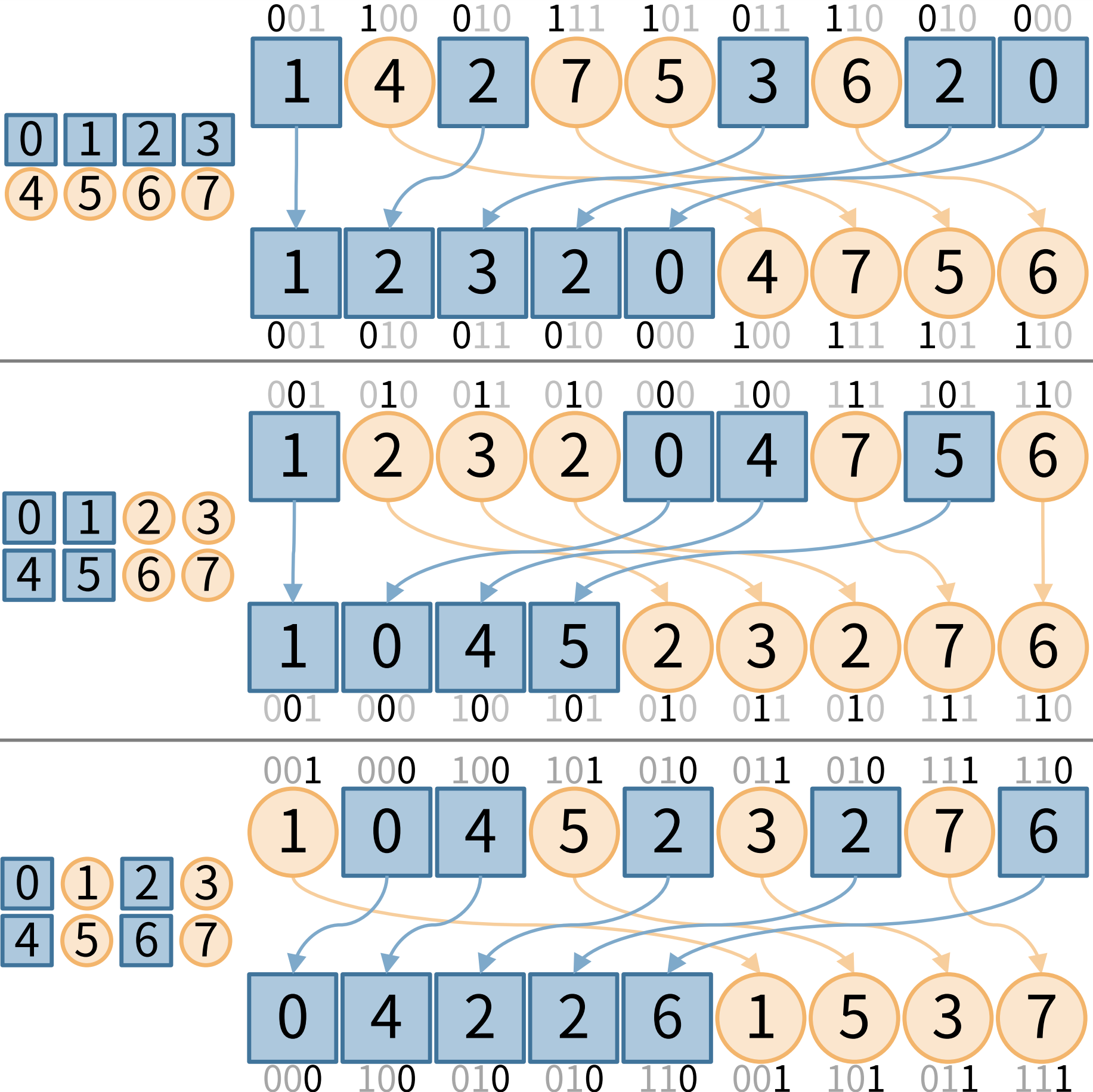
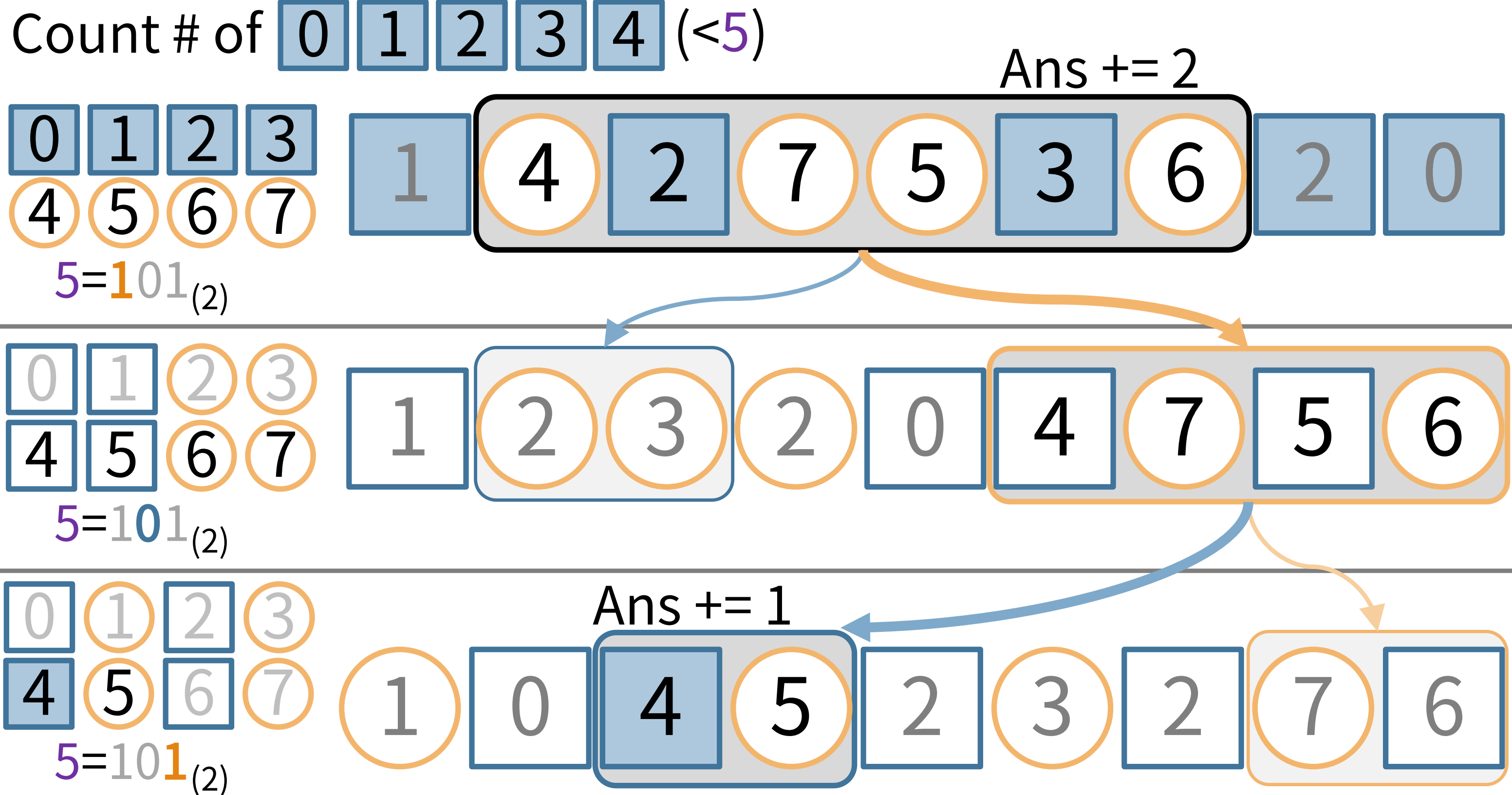
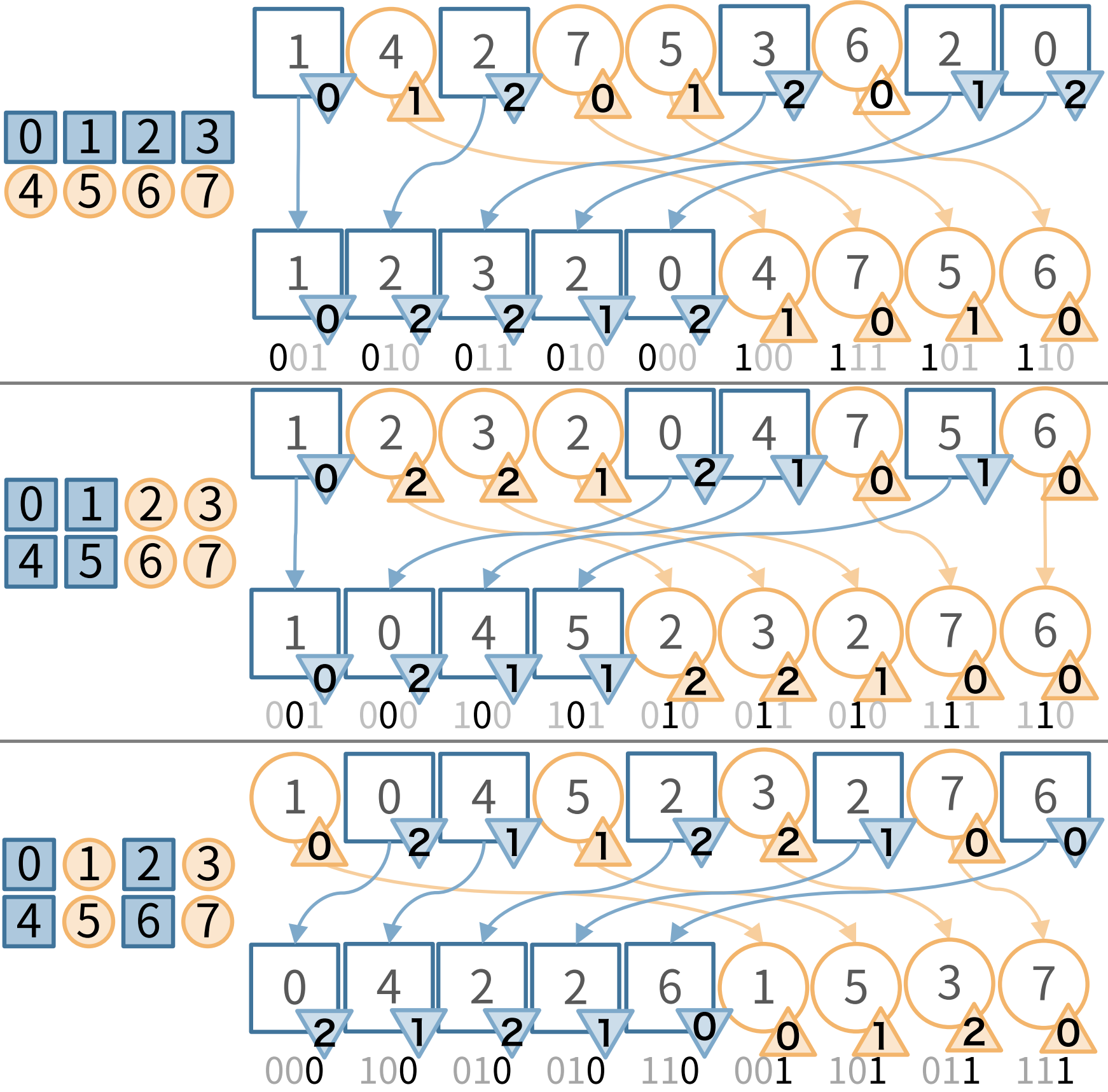
長さ 9 の 3bit整数配列 [1, 4, 2, 7, 5, 3, 6, 2, 0] を例に、実際に構築の手順を見ていきます。

まず、上段では、下から3ビット目が 0 なのか 1 なのかで青とオレンジに色分けされています。これを、同じ色同士の順序は変えずに、青は前方、オレンジは後方に並び替えます。

次に中段では、下から2ビット目が 0 なのか 1 なのかで青とオレンジに色分けされています。これを同様に並び替えます。
最後に下段では、最下位ビットが 0 なのか 1 なのかで青とオレンジに色分けされ、同様に並び替えられています。

基数ソートと処理が似ていると言いましたが、最終的なデータを見ると、2進数の上下の位を反転させる（Bit Reverse する）とソート済み配列になっていることに気づくと思います。

ウェーブレット行列は、このソート時の、並び替える直前の青とオレンジ、つまり0/1のビットだけを記録します。

この青かオレンジかのビット配列だけを用いて、各クエリを省メモリに高速に答えます。

Quantile クエリ : 区間の中で k 番目に小さな値を求める

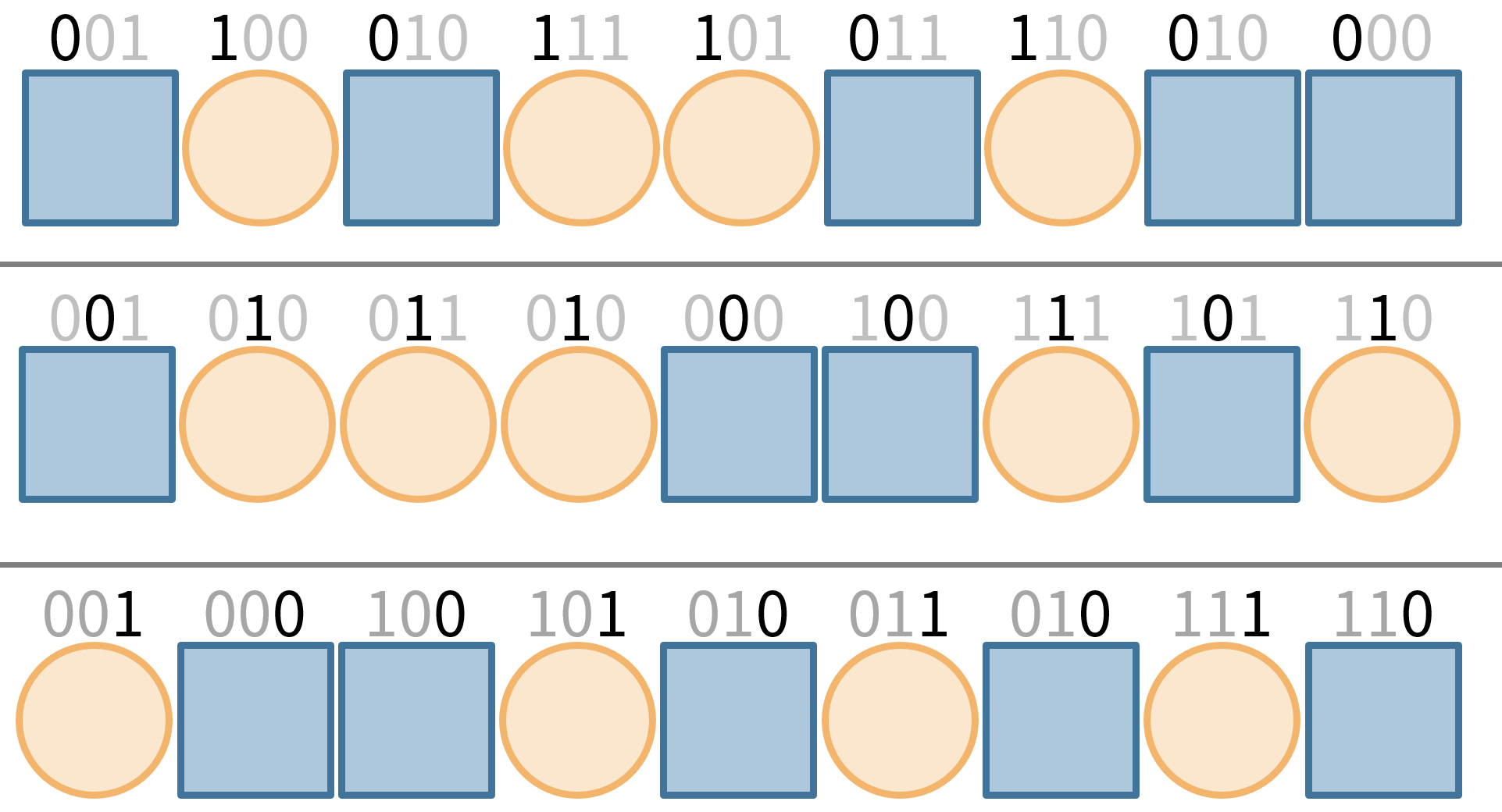
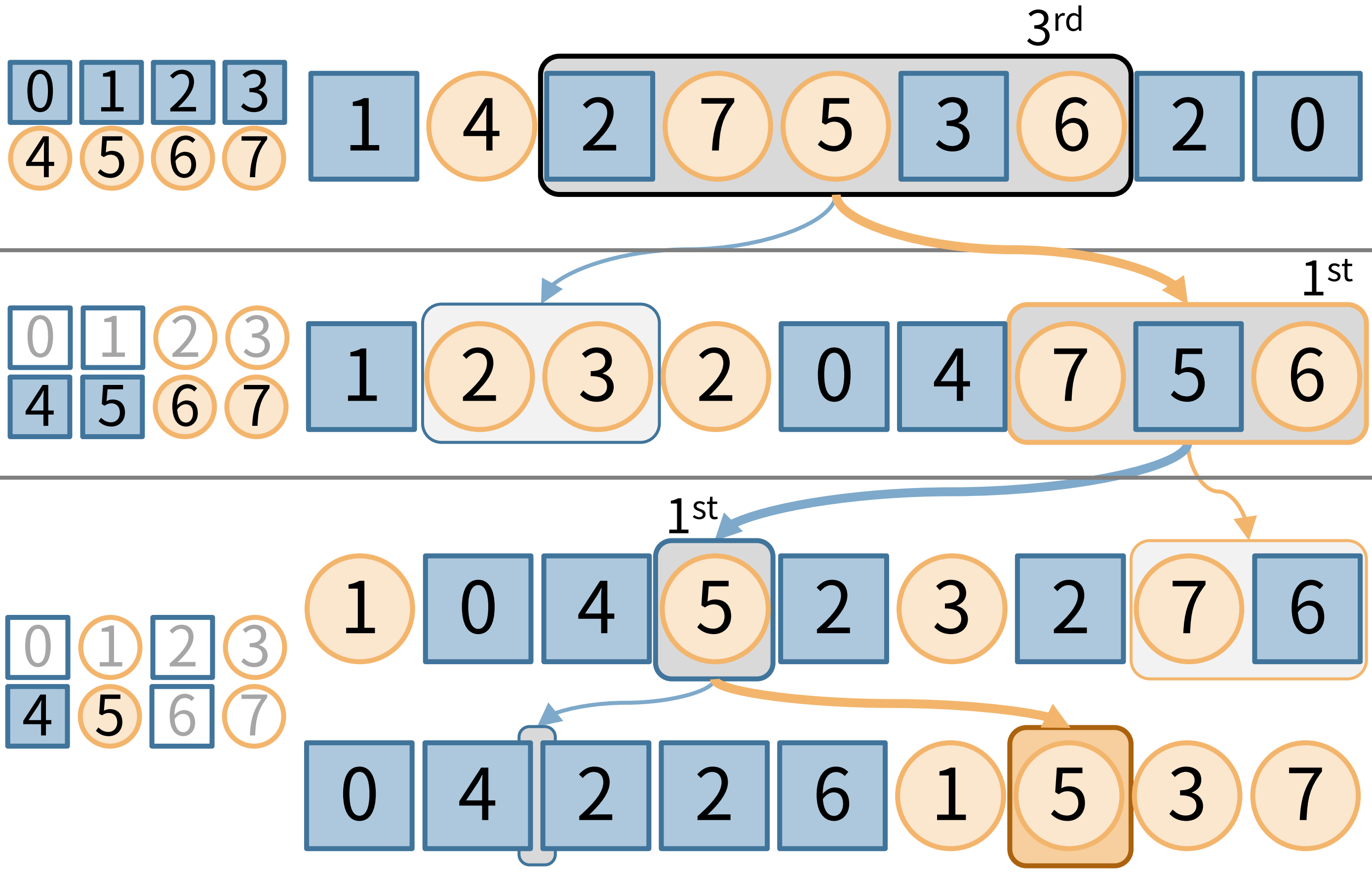
次に Quantile クエリの計算方法について紹介します。例として、区間の3～7番目の5要素の中から、 3 番目に小さな値を図例を使いつつ求めてみます。なお、この図ではわかりやすさの為に数字も振っていますが、前章のとおりウェーブレット行列では青であるのか、オレンジであるのかしか分かりません。

まず、上のビットから考えていきます。図を見るとこの中に青の個数は 2 つあります。
青の値はオレンジの値より小さいということを考えると、この中で 3番目に小さな値というものはオレンジの値であることがわかります。更にいうとオレンジの中で1番小さな値が、目的のものと言うことが分かります。
ここで、特定区間中の青の個数を求める必要が出てきますが、$O(1)$で求める効率的な方法を後章で説明します。

次の段に移ります。1段目の検索区間の要素は青かオレンジかで前後に分かれました。オレンジの値に注目したいので、2つに分かれたうちオレンジの区間に注目します。この区間移動の計算は、1段目全体の青の個数と、1段目の検索区間より右の青の個数、1段目の検索区間内の青の個数を用いることで計算できます。
分かれた2段目の検索区間に含まれる値は、4,5,6,7 の4通りです。この検索区間では、4,5 だけが青であり、6,7 がオレンジになります。
この検索区間で青の個数を数えると 1 つです。2段目の検索区間で、1番小さな値が知りたいので、目的の値は青、つまり 4 か 5 であると言うことが分かります。

同様の手順で次の検索区間、つまり2段目で青に分類された値が集まる3段目の区間に移ります。
3段目の検索区間では、値は 4 か 5 の2通りであり、4であれば青、5であればオレンジになっています。
この区間で青の個数を数えると、0個です。目的はこの区間で1番目に小さな値で、青は0個なので、求めていた答えはオレンジであることが分かります。

この3段目の検索が終わった時点で、答えになる値というのは 5 ただ一つに絞られました。これによって、答えは 5 と求めることができます。

今回は例を使って説明していきましたが、配列や検索区間の長さがどんなに長くても、中のデータがどの様な値でも（整列されてても偏りがあっても）、3 bit 値の配列であれば 3 ステップでこの様に求めることが出来ます。

ここで重要なのは、1ステップ目で答えになりうる値の範囲を 0～7 の 8個から 4～7 の 4 個へ、2ステップ目で 4～5 の 2個へ、3ステップ目で 5 の 1個へ、1ステップごとに半分にしていった事により、定数ステップ数で求められたことです。

RangeFreq クエリ : 区間の中で特定値域のものの個数を求める

次に、区間の中で特定値域のものの個数を求める RangeFreq クエリの計算方法です。
区間 [L,R) で値域が [x, y) の 個数を求める RangeFreq(L, R, x, y) を、値域が [0, x) の 個数を求める LowFreq(L, R, x) 関数を用いて、以下のように変形します。
$$
RangeFreq(L, R, x, y) = LowFreq(L, R, y) - LowFreq(L, R, x)
$$
この様に RangeFreq クエリは、値が x 未満の個数をカウントする LowFreq を用いる事で実装可能です。
LowFreq の計算方法を、例として区間の2～7番目の6要素の中から 5 未満の個数を求める方法を、図例を使いつつ求めてみます。
ここで重要なのは、この $x$ を二進数で上のビットから注目して考えることと、5 未満の個数 を求めるということは、 0, 1, 2, 3, 4 の 5 種類の値のカウントを行うわけですが、0, 1, 2, 3 と、4 の 2 ブロックに分けてカウントするのがポイントです。

まずはじめに、上段から見ていきます。$5 (=x)$ の最上位ビットは $5_{(10)} = 101_{(2)}$ なので 1 です。注目しているビットが 1 のときは、答えを格納する変数 $Ans$ に、区間内の青の個数を加算します。この例では、青の値というのは区間内の 0, 1, 2, 3 の値の個数をカウントしていることになります。

次の検索区間に移るときは、注目しているビットが0であれば青（左）の方向に、1であればオレンジ（右）に進みます。今回は 1 だったのでオレンジの方向に進みます。

中段に関して、$5$ の 2ビット目 は 0 です。注目しているビットが 0 のときは $Ans$ には何もせずに、青の方向に移動します。

最後に下段、$5$ の 最下位ビットは 1 です。1 なのでこの区間中の青の個数を $Ans$ に加算します。この区間の青というのは 4 の個数なので、最終的に $Ans$ には 0～4 の5種類の値の個数が、漏れも重複も無くカウントできたことになります。

BitVector

さて、ここまで Quantile クエリと RangeFreq クエリについて説明してきました。説明の中で指定区間内の青の数(ビットが0の要素数)を数える操作が頻出していましたが、区間 [L,R) のカウンティングには愚直には $O(R-L)$ の時間がかかってしまいます。

長さが $n$ の bool 配列に対して、事前に $O(n)$ かけて累積和テーブル $A$ を用意しておくことにより、区間 [L,R) のカウンティングは $A[R] - A[L]$ を計算すればいいだけであり、$O(1)$ の時間で取得できます。

めでたしめでたしとしたいところですが、累積和テーブル $A$ は、$n$ が int32 で表現できる範囲だとして、$32n$ ビット必要になります。元々の bool 配列のサイズが $n$ ビットであることを考えると、少し大きいです。これはこれで良いのですが、もう少し効率の良い方法を考えます。

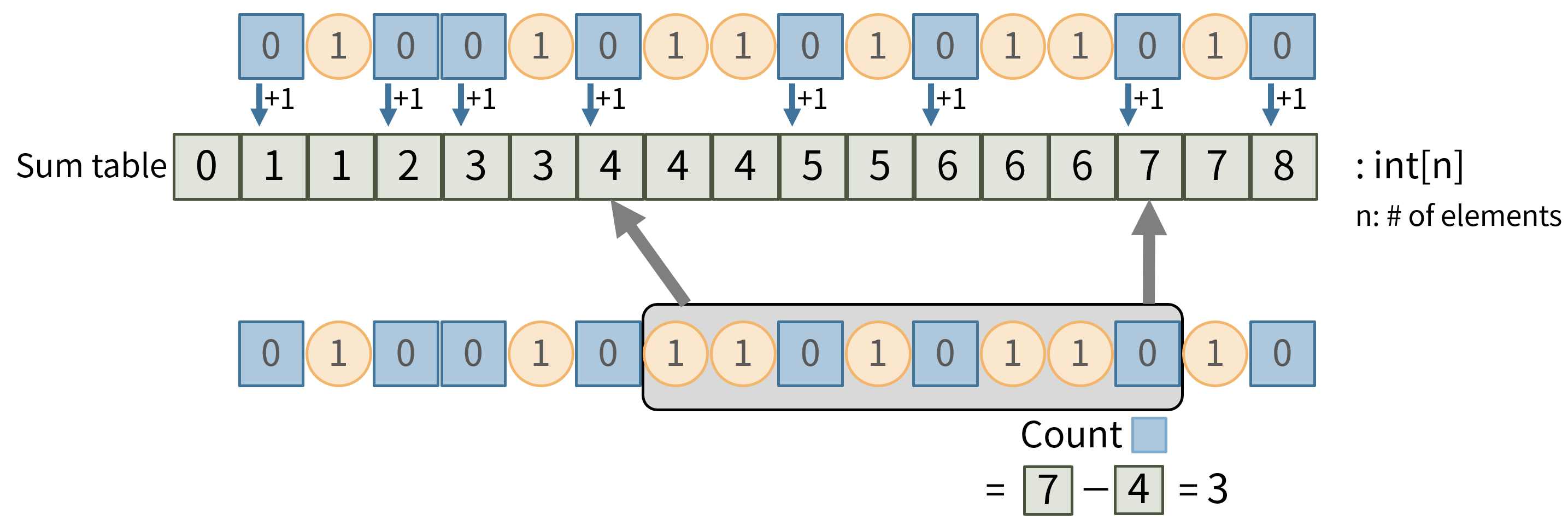
ここで、長さ $w$ ごとに 1 チャンクとして、チャンクごとにそれ以前の累積和と、チャンク内の bool を保持します。PopCount命令（2進数で見たときにビットが1の数をカウントする命令）で扱いやすい様に $w =$ 32 か 64 を一般に使用します。以下の図では $w=$4として説明しています。

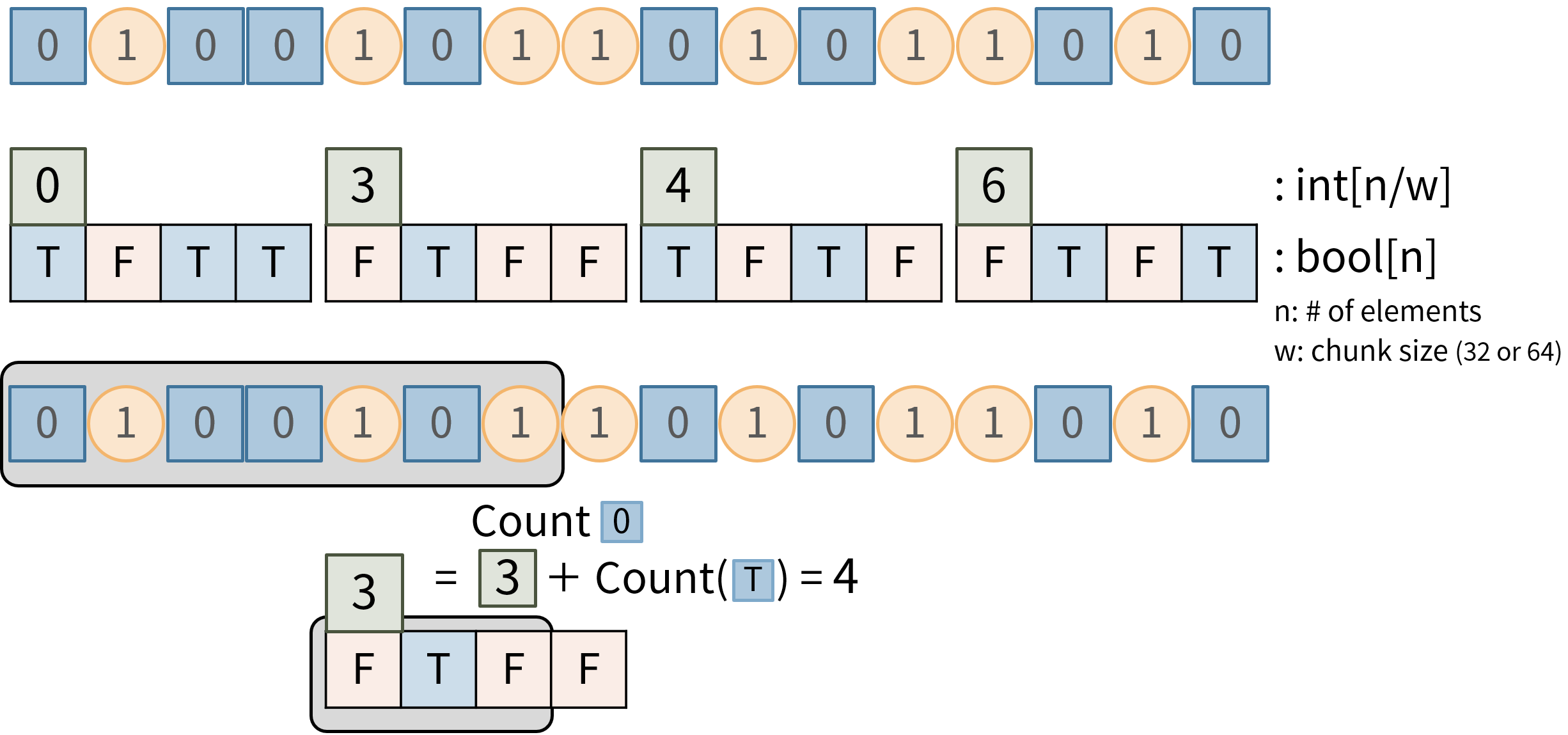
ある地点までの累積和を求めるのは、対象チャンクに書かれている累積和値と、チャンクの対象ビットまでの PopCount の合計を計算すれば求められます。上の図では先頭7ビットの PopCount を、$\lfloor7/w\rfloor = 1$番チャンクに書かれている 3 と、$7 \bmod w = 3$ ということで対象チャンクの3ビット目までの PopCount の合計ということで 4 と求めています。実際、先頭7ビットの青(0)の個数は 4 個です。チャンク内の $x$ ビット目までの PopCount は、$x$ に応じてシフト演算や BZHI 命令を使用して必要な長さに切り取り、PopCount 命令 (CUDA では __popc、GCC では __builtin_popcount など)を使用して計算できます。

このとき必要な空間は、チャンクごとの累積和に $32n/w$ ビット、チャンク内の bool として全体で $n$ ビット必要になります。$w=32$として全体で $2n$ ビットとなり、大幅な効率化が出来ました。
近年のアーキテクチャでは計算がメモリ速度律速になることが多く、メモリ使用量の削減は速度の面でもメリットがあります。

今回はチャンクを1段階で分割しましたが、2段階で分割することにより、メモリ使用量を $n + o(n)$ ビットに削減することができ、簡潔ビットベクトル(完備辞書, BitVector)と呼ばれています。この簡潔とは、実装がシンプルと言う意味ではなく、計算機科学の用語で情報理論的下界に「近い」領域量だけを使いつつ、（他の圧縮形式とは異なり）効率的に質問を受け付けることができるデータ構造を指します。
1段回チャンクの場合は $O(n)$ の空間が必要になるので、簡潔 ではなく コンパクト と呼ばれます。
この程度の完備辞書の用途の場合は、無理に簡潔にしてメモリ使用量を少し減らすよりも、1段階のコンパクト実装にするほうがメモリアクセス回数を3回から2回に減らす事によるメリットが上回り、一般に高速になります。

簡潔ビットベクトルについてより詳しく知りたい方は、以下の記事を御覧ください

• 簡潔ビットベクトル(完備辞書) Tiramister's Blog

3. 提案手法：2次元整数配列を扱えるウェーブレット行列

この様にウェーブレット行列では、1次元整数配列に対しての様々な区間クエリを、効率的に求めることが可能とわかりました。特に、区間の k 番目の数を求める Quantile クエリを用いることで、k を奇数長区間の半分の値にすることで中央値を求めることが可能です。

しかし、画像データのような2次元整数配列に対して応用を考えた時、そのままではうまくいきません。
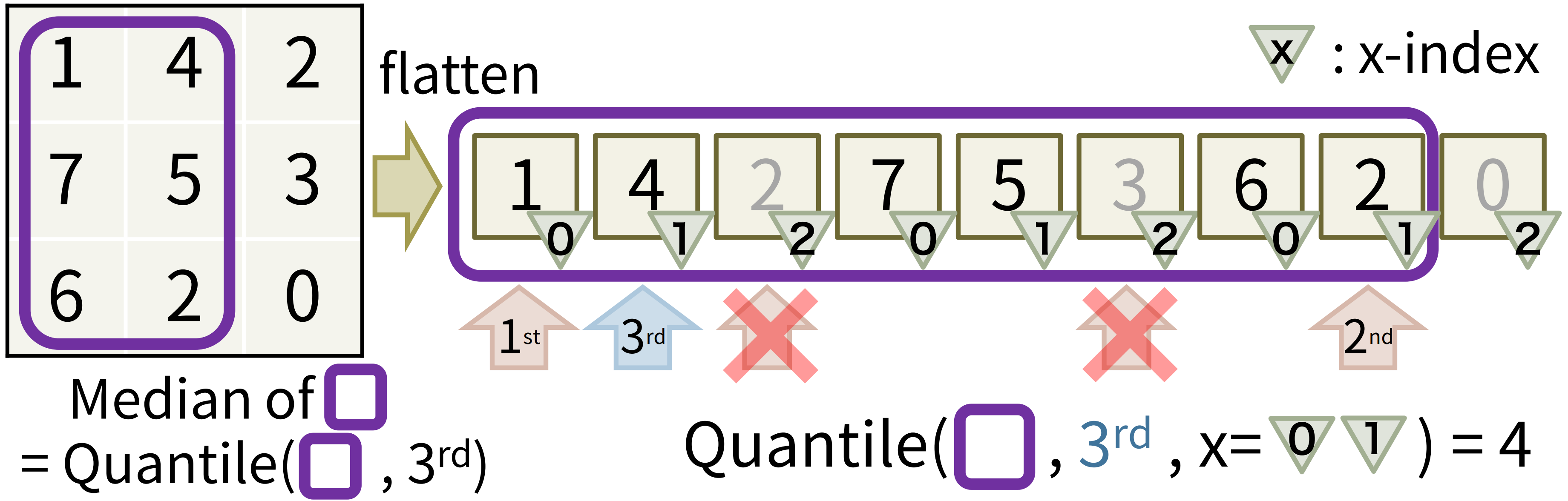
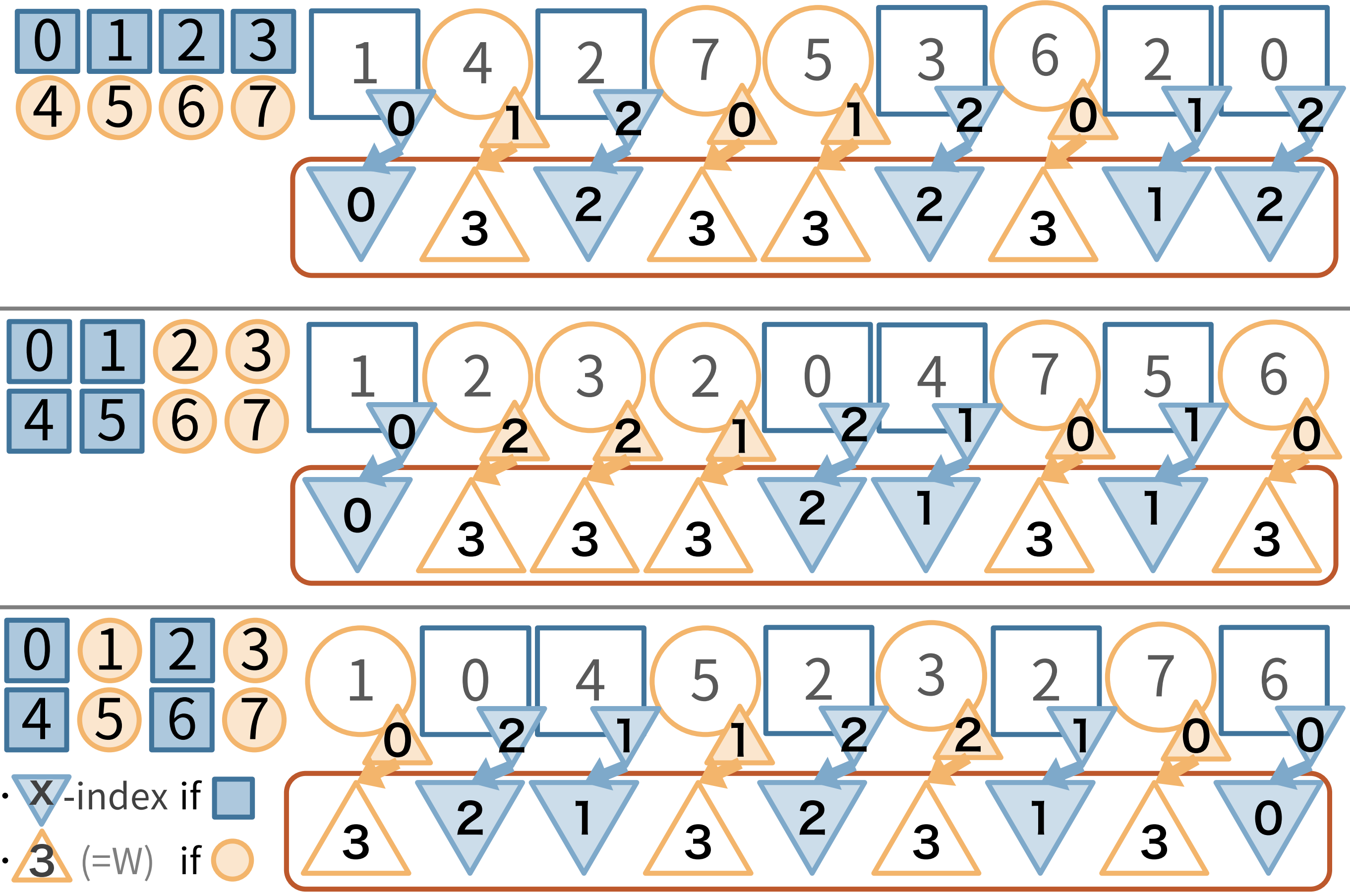
以下の図の様に、2次元整数配列を、1次元整数配列に平坦化してみましょう。1次元に平坦化する時、もともとのマスの x 座標も一緒にメモしておきます（図で言う各マスの右下の三角内の x-index のこと）。

この時、元々の 2 次元配列における矩形区間を、そのまま 1 次元配列での区間にそのまま言い換えようとしても、途中に不要なマスが含まれてしまうのでうまくいきません。図の例でいうと、2次元の矩形区間では x 座標が 0～1 であるものの中で 3 番目の値を求めたいわけですが、1次元にそのまま当てはめようとすると不要なx座標が 2 であるものも含まれてしまいます。

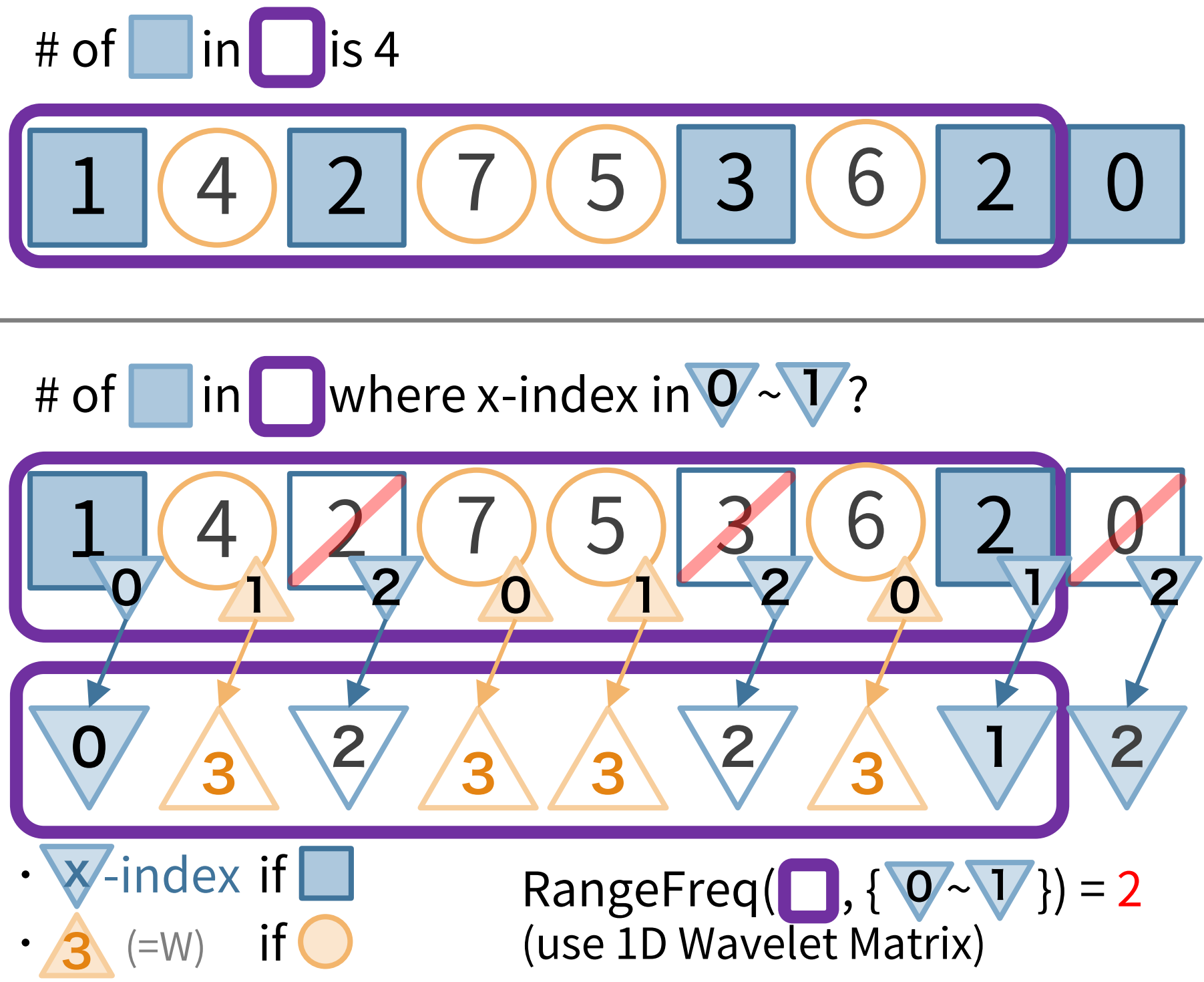
ここで、1次元のウェーブレット行列での操作を振り返ってみます。1次元のときは、範囲中の青のマスの個数を数えるのが重要な操作でした。2次元のときに、x座標が不要なものは無視してカウントしたいです。

ここで、青のマスはそのまま x 座標、オレンジのときは $W$ (=画像の幅。つまりいかなる x 座標よりも大きな値) に置き換えた新たな数列を考えます。
これに対して、区間内の 0～1 の値の個数を数えることで、x座標が0～1であった青のマスの個数を数えることができます。
この操作は、1次元ウェーブレット行列における RangeFreq と同じ操作になります。
つまり、内部に 1 次元ウェーブレット行列を保持しておくことで、2 次元整数配列に対するウェーブレット行列が実現可能なのです。

2次元ウェーブレット行列の構築

前章のアイディアをもとに、2次元ウェーブレット行列の構築を考えてみます。
まず、2次元配列を、x座標を添付して平坦化します。そして、それぞれの値を、x座標を付加したまま1次元ウェーブレット行列の構築をしたときと同様にビット数分並び替えを行います。

1次元ウェーブレット行列のときは、並び替えた数値の青かオレンジかの 0/1 のみを保存していました。
2次元ウェーブレット行列では、青のときはx座標、オレンジのときは $W$ に並び替えた数列を作ります。クエリ処理の時、この数列に対して RangeFreq を行いたいので、この数列で1次元ウェーブレット行列の構築を行います。
$b$-bit 値の値を扱う2次元ウェーブレット行列では、$b$ 本の1次元ウェーブレット行列を内部に持って、クエリに答えていきます。

2次元 Quantile クエリ : 区間の中で k 番目に小さな値を求める

では実際に、2次元整数配列における Quantile クエリを考えて行きます。
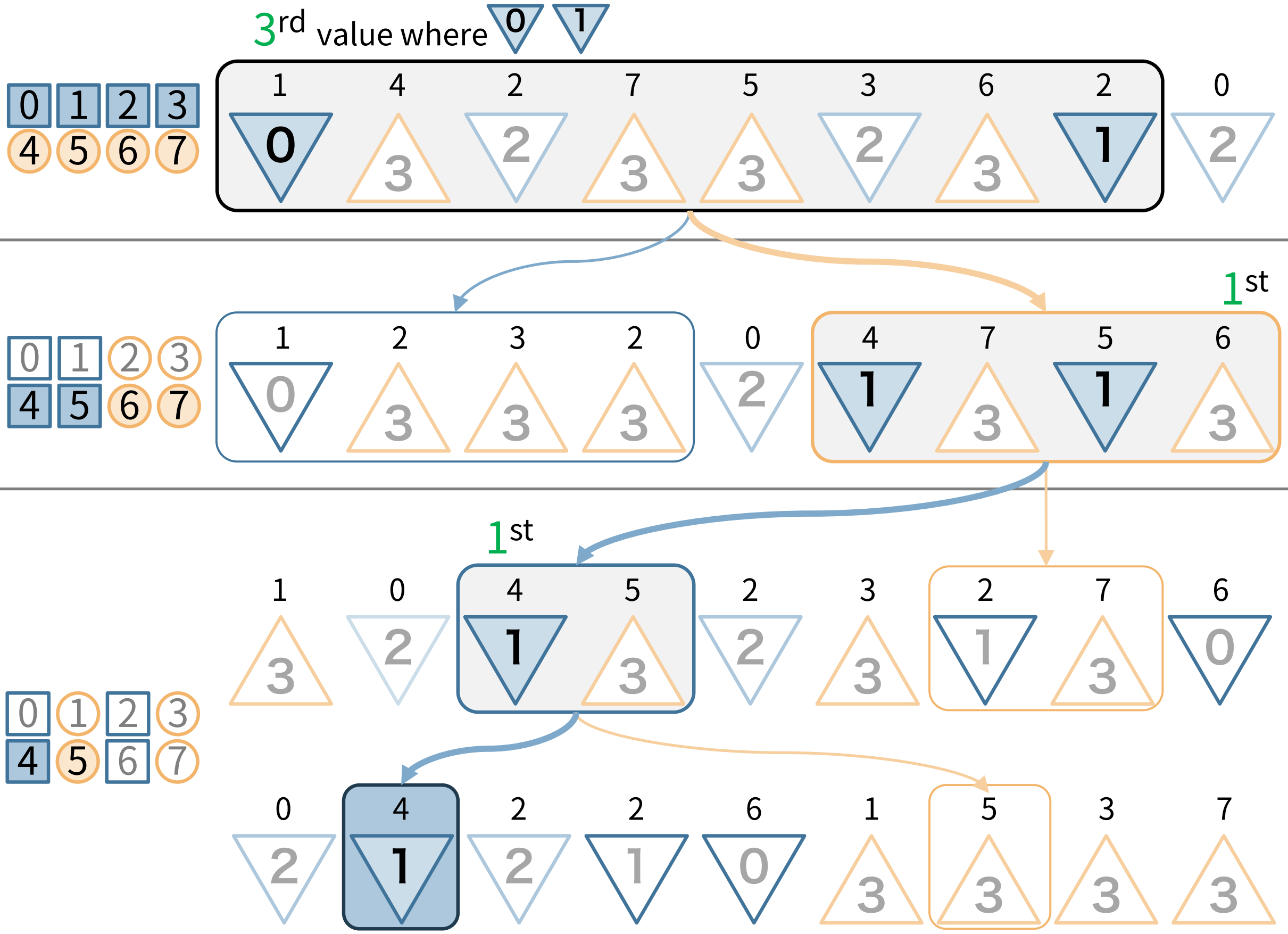
例として、3x3 マスの入力画像に対してx座標が0～1、y座標が0～2の6マスの矩形区間の中央値を求めてみます。なお、偶数個要素の中央値は本来、$n/2$ 番目と$n/2+1$番目の値の平均を採用するのが一般的ですが、今回のメディアンフィルタでは簡単のために $n/2$ 番目の値だけを採用することにします。
今回の例の場合、1, 4, 7, 5, 6, 2 の中で 3 番目に小さな値を求めます。

1	4	2
7	5	3
6	2	0

1次元ウェーブレット行列のときと同様に、上のビットから考えていきます。
まず、最初の検索区間です。RangeFreq クエリを使えば、対象区間中の 0～3 の値の個数が分かります。実際に 1D-RangeFreq でx座標 0～1 の個数をカウントすると 2 になります。 もとの数列の対象区間を思い出すと、 1, 4, 7, 5, 6, 2 なので、実際に、対象区間中の 0～3 の値の個数は2個であることが分かります。
3番目に小さな値を求めたかったので、答えは後半のオレンジにあることがわかるので検索区間を移動し、この中で1番目に小さな値を求めます。

次に2段目です。この区間で x座標 0～1 の個数をカウントすると 2 です。これは、もとの数列における 4・5 の値の個数に相当します。1, 4, 7, 5, 6, 2 なので一致します。答えは前半の青にあることがわかるので検索区間を移動します。

最後に3段目です。この区間で 1 番小さな値を求めます。x座標 0～1 の個数をカウントすると 1 で、これはもとの数列における 4 の個数です。1番小さなものを求めたかったので、答えは前半の青、つまり 4 に絞られます。3ステップ目が終了し、3-bit 二次元配列であったのでこれで手順は終了です。1, 4, 7, 5, 6, 2 の中で 3 番目に小さな値は 4 ということが分かりました。

計算量

$W \times H$ の二次元配列を一次元配列に平坦化すると、長さが $WH$ の一次元配列になります。
$b$-bitの値を持つ二次元ウェーブレット行列は、内部に値域が 0～W で長さが $WH$ の一次元ウェーブレット行列を $b$ 本持っていました。長さが $n$ で値域が$[0, m)$ の一次元ウェーブレット行列の構築時間は $O(n\log m)$ であったので、二次元ウェーブレット行列の全体の構築に必要な時間は $O(bWH\log W)$ になります。

空間計算量に関しては、Compact な Bit Vector を使用する $b$-bit 値で長さが $n$ の一次元ウェーブレット行列は $O(bn)$ の空間が必要であるので、二次元ウェーブレット行列の全体で $O(bWH \log W)$ の空間が必要になります。

32bit float への対応

これまでの説明では、入力は整数であることを前提としていました。しかし、画像処理では、ピクセルを float で処理するシーンも多々あります。
float 型が一般的に用いられている IEEE 754 形式であることを仮定すると、非負の画素しか登場しない場合は、float 32 のビットパターンを uint 32 として解釈しても、nan を除いて値の大小関係が保存されるので問題ありません。しかし、負の値の画素が含まれる場合、符号ビットに応じて追加の処理が必要になります。

ここで、一般に入力画像の画素数は一般に $2^{32}$ 以下であることを利用します。（縦横 $65536 \times 65536$ pxのときに、ちょうど $2^{32}$画素）
入力の画素全体を、値と座標をペアにソートして、それぞれの値が何番目に小さな値なのかで置き換えます。（このとき、値の重複を削除する必要性はありません）
例えば $2048 \times 4096$ サイズの画像の場合、各ピクセルは $0$～$2^{23}-1$ の値に変換されます。これは 23-bit 整数を扱うウェーブレット行列として処理することができ、32bit として扱うよりも 23/32=0.71875 だけ高速化されます。
最後に、テーブル引きをして元の float の値に戻せば完成です。
ソートやテーブル引きのコストが増えてしまいますが、ソートなどは非常に研究されつくされ高速に行うことができるので、非負の画素しか登場しない場合でもソートを行った方が高速になります。

矩形窓以外への対応

これまでの例では、軸に沿った四角形の範囲で中央値を求めている例になります。しかしメディアンフィルタの派生として、六角形や八角形範囲の中央値を取る事で、より綺麗な結果を得られる事があります。
今回のウェーブレット行列を使った手法でも、時間やメモリが2倍必要になってしまいますが六角形範囲、3倍必要になりますが八角形範囲、5倍必要になりますが十二角形範囲にフィルター窓を拡張することが出来ます。詳しくは論文の p12、Appendix B を御覧ください。
また、六角形範囲の実装例もあります。六角形であれば四角形よりも十分円形に近いので実用的でしょう。

4. 評価 (Result)

今回の二次元 Wavelet Matrix を用いたメディアンフィルタを CUDA で実装し、NVidia 製 GPU 上で実行できるようにし評価を行いました。環境としては以下のとおりです。

GPU	NVIDIA GeForce 3090 RTX
CPU	Intel Core-i9-9900X
OS	Ubuntu 20.04 LTS

詳しくは こちらのGitHub上の情報 を確認ください。

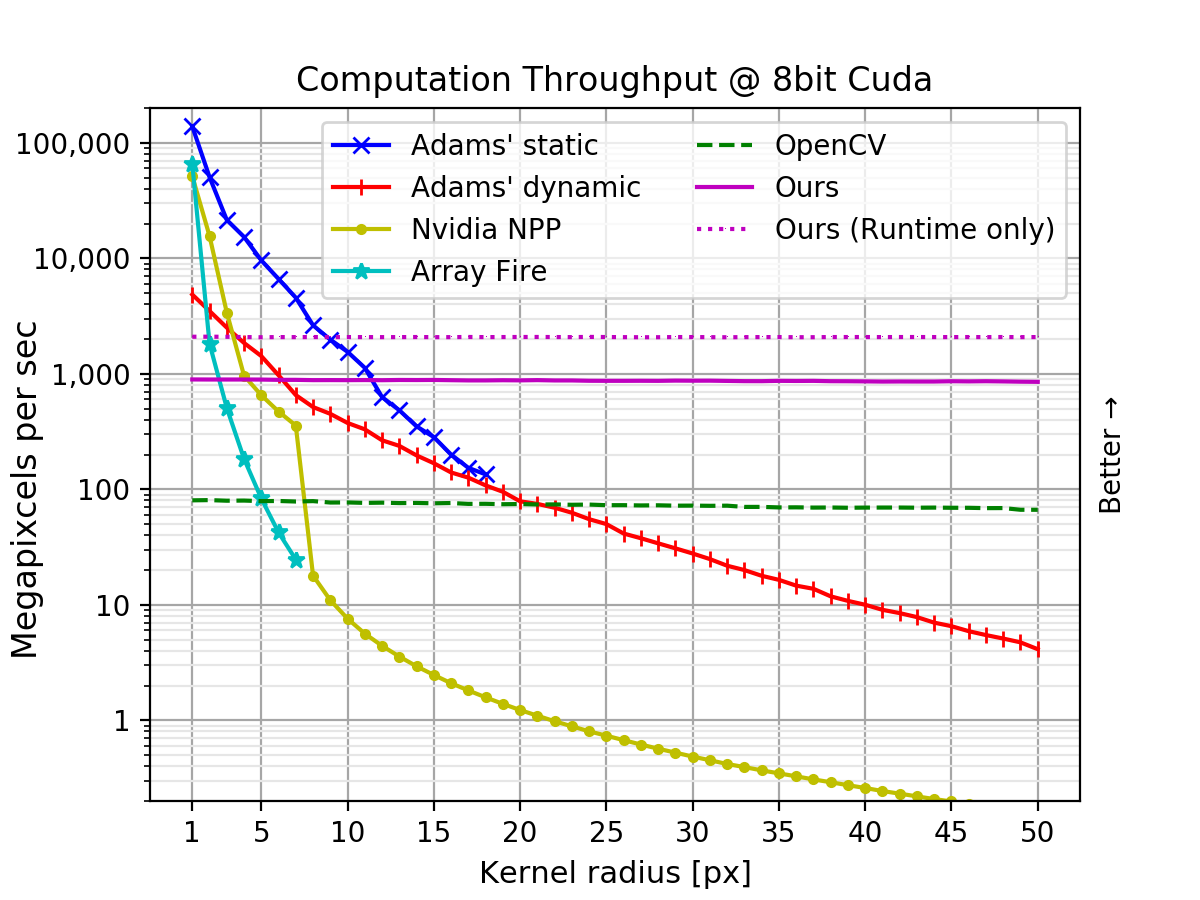
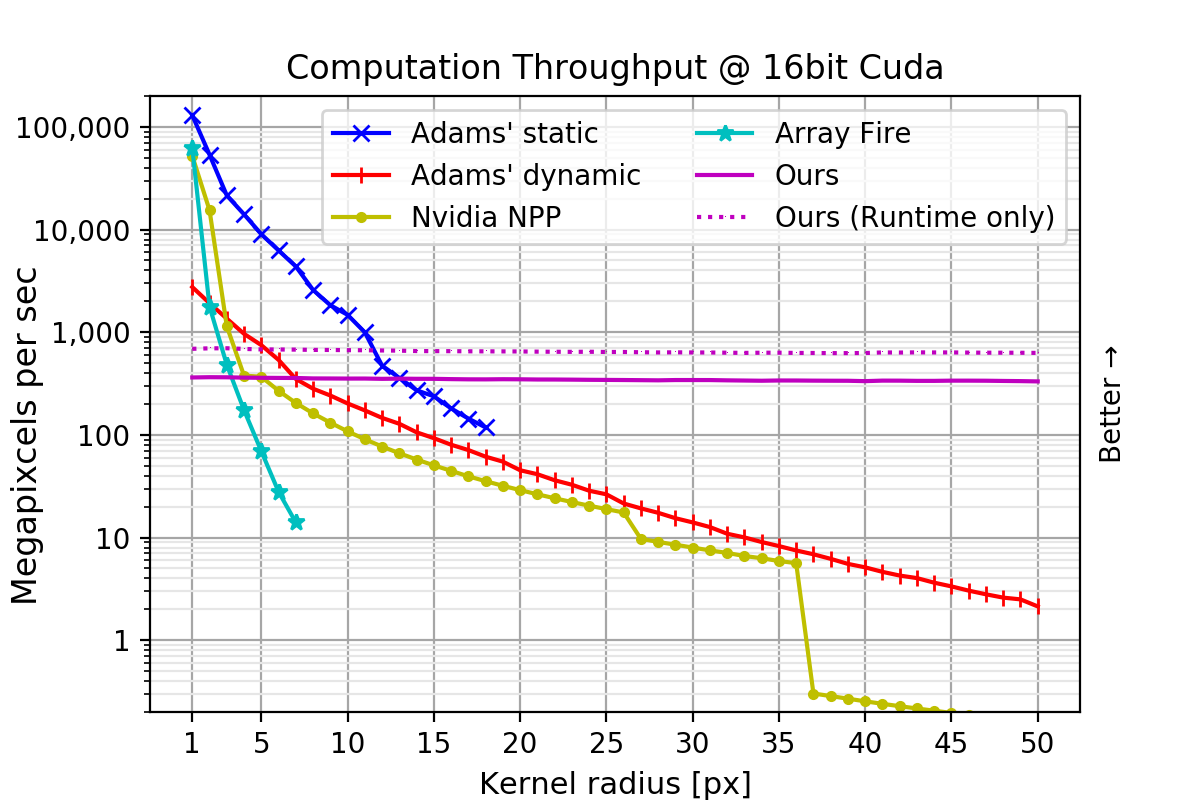
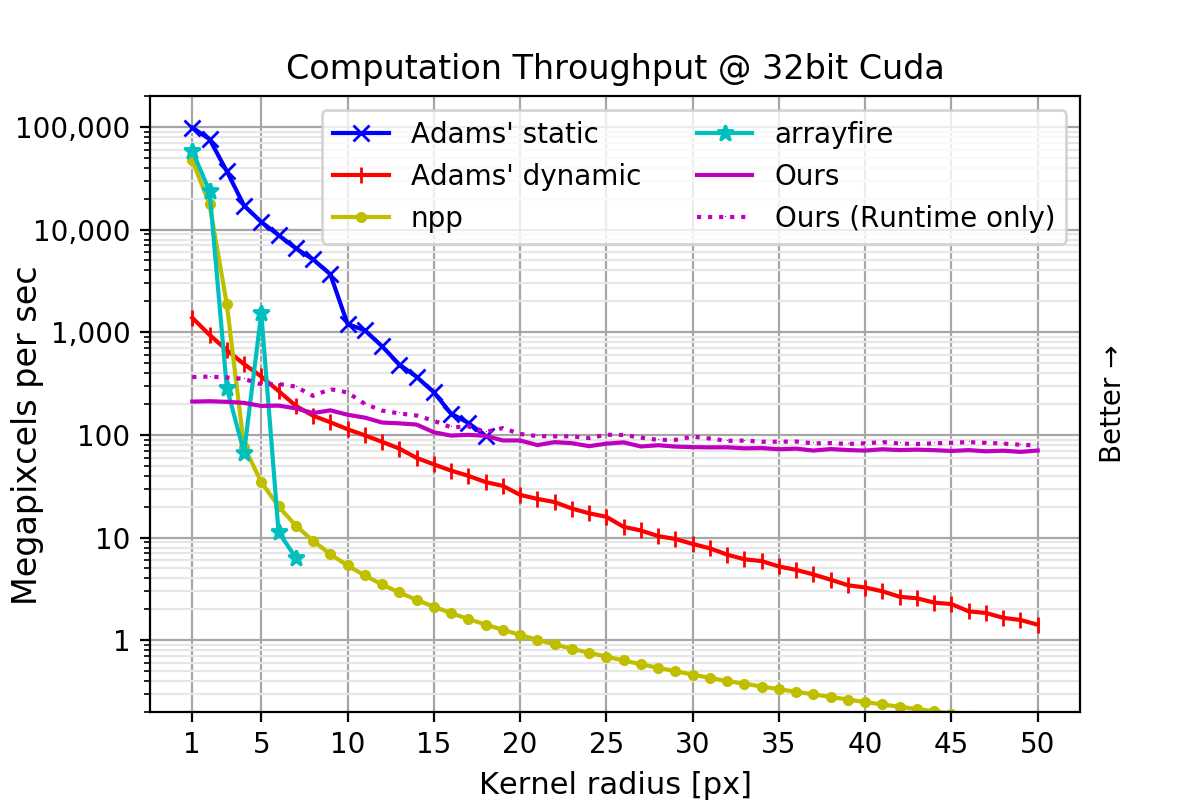
3840×2160 ピクセルの 4K サイズの 8-bit int, 16-bit int, 32-bit float 画像を用意し、画素数を固定してフィルター半径を変えてそれぞれのフィルタ速度を比較しました。
単位は横軸がフィルタ半径[px]であり、縦軸がスループット(Mega 画素)、つまり1秒間に何百万ピクセル相当を処理できたかを表しています。つまり高いほど良い成績であり、1000 Mega 画素を達成した場合は、1000x1000 画素を 1msで、3840×2160 画素を8.29msで処理できたということを表します。

比較に用いた手法を簡単に紹介します。

• Adams : ソーティングネットワークを用いたソートベース最速の実装です。SIGGRAPH 2021 に発表されました。dynamic はソーティングネットワークを実行時にインタプリタ的に構築・実行しています。static はコンパイル時にフィルタ半径を固定することにより、特化したバイナリを Halide を用いて生成します。非常に高速ですが半径14のコードをコンパイル生成するのに5分、半径18の生成に30分かかり、それ以上は当環境ではコンパイルが不可能でした。
• Nvidia NPP: NVidia による画像処理ライブラリ 2D Image And Signal Performance Primitives (NPP) です。CUDA 上で高速に実行できるようにチューニングがされています。
• Array Fire: オープンソースの画像処理ライブラリです。
• OpenCV: オープンソースの画像処理ライブラリです。CUDA用はヒストグラムベースの手法が使われており、NVIDIA Research の Green 氏が 2017年に実装・論文を公開しています。

提案手法の Ours はウェーブレット行列の構築と中央値計算の両方を含んで計測しています。Runtime Only は 構築にかかった時間を無視し、構築済みのウェーブレット行列を利用したときを想定した時間です。同じ入力画像に対してフィルタ半径を変えるなどのユースケースにおいては構築済みウェーブレット行列を使い回すことができます。

実際の結果は以下の通りです。

提案手法はフィルタ半径が変化しても計算時間が変わらない、定数時間フィルタリングを実現しています。
8ビット画像のとき、提案手法は半径12以上で最速となっています。また、半径50の時はソート法最速の Adams 氏の手法と比べ 206 倍高速でした。計算時間が半径に依存しない OpenCV のヒストグラム法と比較すると、どの半径のときでも 11 倍程度以上高速でした。

16, 32bit 画像の場合、それぞれ半径13, 15 以上で提案手法が最速となりました。半径50のとき、次点の Adams 氏の手法と比べそれぞれ 155倍、50倍高速でした。
ヒストグラム法による OpenCV では 8bit 以外対応していませんでしたが、提案手法はこの様な HDR 画像に対しても定数時間フィルタリングを実現しました。

同じ入力画像に対してフィルタリングを想定した提案手法の Runtime Only では、8ビット画像のとき半径 9 以上で全手法の中で最速の手法となりました。

メモリ消費量

Full HD、4K サイズのそれぞれのモノクロ画像に対し、各色ビット数でウェーブレット行列を構築するときに消費したメモリ使用量 [MB] は以下の通りでした。

画像サイズ	1080 x 1920			2160 x 3840
色ビット数	u8	u16	f32	u8	u16	f32
WM本体サイズ	50 MB	100 MB	139 MB	216 MB	431 MB	653 MB
構築時追加バッファ	79 MB	149 MB	199 MB	315 MB	597 MB	863 MB

8bit の 1080p サイズであれば、50+79=129 [MB] のメモリがあれば使用可能であることがわかります。4Kサイズになったとしても 216 + 315 = 531 [MB] と、およそ画素数に比例したメモリ使用量でフィルタリングが可能です。
16bit の時は、8bit の倍程度のメモリ使用量でした。32bit Float の場合、一旦画素のソートを行ってから番号を振り直しているので 8bit の 4倍よりはメモリ消費量を抑えられています。4K 32bit のとき、合計で 1.5 GBのメモリが必要でした。一部の GPU ではビデオメモリが不足する可能性がありますが、4K HDR を扱うような環境では相応の GPU を使用していることを期待すると現実的な消費量と言えるでしょう。また、ウェーブレット行列の構築は CPU 側で行い、実際のフィルタリングはデータ構造を GPU に転送してから行うヘテロジニアスな手法を使用すれば、GPU 側のメモリは 653 MB ですみ、CPU と GPU の両計算資源を有効活用できる可能性もあります。

5. 制約と今後の課題

メモリ使用量

8bit の RGB 3チャンネル 1080pサイズ の場合、約 387 MB のメモリが必要です。しかし4K 32bit カラーの場合、全チャンネル同時に処理をしようとすると約4.5GBのメモリが必要になります。4K 画素レベルであれば1チャンネル毎に処理しても実装にもよりますが約25万から800万のスレッドが発生するので、現代のGPUのスレッドを十分有効活用できる量ではあります。しかし、いくら 4K HDR 自体高コストな内容だとしても、少し大きすぎるかもしれません。

現在、メモリ使用量を約半分にするマイナーアップデート手法が発見できたので、実装が完了次第プロジェクトページなどで成果を追記します。

CPU 版の実装

今回、CUDA 向けの効率的な実装は行い、実際に高速に動作することを確認しましたが、CPU 版の効率的な実装は（時間が足りないのもあり）行いませんでした。なお、可読性を優先した現在の CPU 版の実装は、OpenCV と比較して数十倍です（実行時間が）。
ウェーブレット行列ではビットベクトルの操作が非常に重要であり、2進数でビットが1の数を求める PopCount を非常に多用します。CUDA ではハードウェアによる __popc 命令があります。CPU でも __builtin_popcount や _mm_popcnt_u32 命令を使用した popcount 命令はあるのですがこれはスカラ命令であり、AVX2 や AVX-512 の様な複数の値を同時に処理する SIMD 化を行おうとしたら使用できません。AVX-512 にも AVX512-VPOPCNTDQ に対応した CPU であればベクトル popcount があるのですが、AMD Zen4 や 省電力向けモバイルノートに使用されている Intel IceLake 系列でしか使用できず、個人向けハイエンドデスクトップ向けの Raptor Lake (Core i9-13900K等)では利用できません。

CPU 版の効率的な実装をしてくれる方を募集しています。

(正確な)メディアンフィルタ以外へのウェーブレット行列の応用

今回、今まで1次元整数配列に利用されてきたウェーブレット行列を2次元整数配列に適応可能な様に拡張し、画像処理にもウェーブレット行列が利用可能であることを示しました。
しかし、メディアンフィルタ以外への応用はあまり目処が立っていません。
グラフィックスの研究者にウェーブレット行列を知っていただく事で、コンピュータビジョン系を含む他の画像処理への応用を期待しています。

また、メディアンフィルタは様々な派生が存在し、中には正確なメディアンフィルタよりも特定用途でより良い結果を得られるものが数多くあります。それらの手法の中にはウェーブレット行列を利用することでより高速化できる可能性もあります。

6. この研究の経緯

ここまでは論文に書かれている事の日本語解説 + 一部補足を行ってきました。ここからは論文には書かれていない研究の背景を紹介します。

私自身の紹介を少しすると、高校時代から情報オリンピックや AtCoder などの競技プログラミングを始めました。2022/12/23 現在、私の AtCoder は黄色であり、AtCoder 内では上位約 1.4%、順位は世界1360位、日本人405位になります。AtCoder 社長 chokudai さんのブログによると

研究職・研究開発などや、高度なアルゴリズムを要求される開発現場で重宝されます。

と紹介されているランクです。個人的には DP やグラフ系の問題が苦手気味ですが、ACM-ICPC と言う国際大学対抗プログラミングコンテスト では、3人で1チームと言う特徴と、重実装・幾何を専門に担当し、運もあり 2018年大会の World Finals に出場しています。
ウェーブレット行列はコンピューターグラフィックス分野の研究者の間では無名なデータ構造ですが、競技プログラミングでは上級者の中では非常に有名なデータ構造であり、知っていました。

また、競プロ以外の趣味として、高校時代から映像制作を行っています。AtCoder社のPVを自主制作したり、ICPC アジア地区横浜大会のオープニング映像を制作したりしています。また、自主制作の二次制作ミュージックビデオがニコニコ動画トップページに紹介され殿堂入り目前だったり、ニコニコ超会議に自分の映像が展示・受賞されたこともあります。

映像制作の経験を積む中で、メディアンフィルタが数多くの表現を構成する要素の1つとしてよく使用されていることや、メディアンフィルタの処理が非常に遅いと言うことを知っていました。

そして私が学部4年生のとき(2019年)に、ウェーブレット行列を使えばメディアンフィルタが高速化できるということに気づきました。
つまり映像制作と言う知見から問題発見を行い、競プロの知見から問題解決を行ったとも言えます。

2021年までは別の研究を行っていたのでネタストックとして取っておいたのですが、そちらも一段落したのでこの研究・実装を本格化しました。
ずっとストックしていた理由の一つに、ウェーブレット行列は計算量こそ良いものの、定数倍が少し遅いと言う経験があり、理論的な計算量が減らせても実際のフィルタ速度も速くなるのか確認が持てなかった事が挙げられます。そのため、最初のうちは SIGGRAPH よりのランクが少し下の EGSR (Eurographics Symposium on Rendering) という学会で発表することを目指していました。
しかし、CUDAの実装・チューニングを進めた結果、GPU上で既存手法の10～100倍以上高速化できることが判明し、SIGGRAPH Asia へ変更しました。

7. 査読の感触

SIGGRAPH Asia 2022 の Technical Paper では5人の査読者がアサインされ、

• Strong Accept(+5)
• Accept(+3)
• Weak Accept(+1)
• Weak Reject(-1)
• Reject(-3)
• Strong Reject(-5)

の6段階で評価されました。私の最初の評価は +3, +3, +3, +1, +1 でした。
主にメディアンフィルタと言う古典フィルタの全く新たな実装を提案した事が特に評価された感触です。
論文の説明に関しては、ページ数の制約もあり、ウェーブレット木の説明ではなくいきなりウェーブレット行列の説明から始めざるを得なかった点で分かりにくい・不十分と意見もありました。一部の査読者は論文だけでは分からなかったが、ウェーブレット行列の説明をしているブログを読んだことで理解できたとコメントいただきました。
大きなツッコミとして、CPU 版の実装は可読性を重視したものしか用意していなかったのですが、それを指して CPU 版の実装を動かしたら非常に遅かったと言う意見がありました。それに対しては CPU 版の効率的な実装は Future Work ということにして納得していただきました。

リバッタル（反駁）を返したあとの評価では、+3, +3, +3, +3, +1 と1人評価を上げていただけました。
+1 とした査読者も特に大きなマイナスがあると言うわけではなく、専門分野でなかったので高評価をつけられないといった印象でした。
平均評価としては +2.6 なので、高い評価をいただくことが出来ました。個人的には Strong Accept(+5) を出す査読者はいなかったが Best Pepar Award をいただくことが出来たのが少し意外と感じました。

8. Best Pepar Award をいただけた事の分析

Best Pepar Award の連絡が来たのは、SIGGRAPH Asia の始まる前日でした。ボスと韓国へ前着し、電車に乗っているときにメールで連絡が来ました。

実はウェーブレット行列を拡張して2次元整数配列を扱えるようにするというアイディア自体はシンプルなものであり、競プロerの中には気づいている人も居ました。このブログでは「3 次元空間の点群」を扱っていますが、これは「2次元整数配列」を扱うと言うのと同義です。正直、論文を書いている最中にこのブログを発見してかなり焦りました。しかし、このブログの公開日、そしてブログ中で拡張ウェーブレット行列が使えると示して 3 TLE 出している問題の提出日が 2021/6/2 です。それに対して私はこの問題に対して、同じく拡張ウェーブレット行列により 2 TLE や AC を 2021/5/31 に行っていました。なので新規性に関して万が一ケチをつけられたとしても一応私の方が先🤔ということで進めました。

（もっとも、論文成果としての主張がされていなければ、この程度では独自性を疑われることはほぼ無いでしょう。例えば高速フーリエ変換の発見は 1965年に Cooley と Tukey が発見した事になっていますが、実は 1805 年頃からガウスを始めとする一部の人は独自に同様の手法を発見していたと言われています。）

このことから、ラマヌジャン的な突拍子の無い超定理を発見した事による評価、では無いと自己分析しています。
自己分析では、以下の点が評価されたと考えています。

• ソート法とヒストグラム法が主流だった古典フィルタのメディアンフィルタの、全く新たな第3の手法を提案した点
• 別の分野で研究されてきたウェーブレット行列をグラフィックス分野に持ち込んだ点
• 単に輸入しただけではなく、（少しの）独自性を用いて拡張している点
• GPU において、実際に10～100倍以上高速化された点

これが達成できた要因としては、競技プログラミングの知識と言う問題解決力の貢献が非常に大きかったでしょう。

9. まとめ

いかがでしたでしょうか。
ACM SIGGRAPH と言うコンピュータ・グラッフィックス分野のトップカンファレンスの Best Paper Award と言う大変光栄で貴重な賞をいただいたので、記念して日本語解説記事を作成しました。
今回の Award は運や、論文執筆を手伝っていただいた指導教員の力も大きかったと考えていますが、アイディア自体は意外とシンプルで、人を超えていないと出来ない業績では無いと思います。
特に私の場合は、映像制作の経験による問題発見と、競プロの経験による問題解決力が重要だったと振り返っています。
競プロが研究解決における万能の要素とは決して考えてはいませんが、多方面の興味を持つ事で、この様な異分野技術を用いて新たな問題解決ができると思います。

ぜひこの記事が修士・博士を始めとする研究生活の知見として活かせたらと思います。

最後に良ければ、この記事のいいね・ストックをお願いします。