前回の記事の続きとして様々な広義積分を数値計算する。
ここでは
y=\frac{2 \arctan(x)}{\pi}
と置くことによって
\int_{-\infty}^{\infty}f(x)dx=\int_{-1}^{1}\frac{\pi}{2\cos^2(\frac{\pi y}{2})}f(\tan(\frac{\pi y}{2}))dy
と変形できることを用いる。
計算に用いるプログラムは以下の通り
#include <stdio.h>
#include <math.h>
double f(double x){
double y;
y=/* ここに計算に使うf(x)の式を書く*/;
return y;
}
double g(double x){
double y;
y = M_PI*f(tan(M_PI*x/2.))/(2*pow(cos(M_PI*x/2.),2));
return y;
}
int main(void){
int i,N=50000;
double S,dx;
dx=1./(double)N;
S=0.;
/*積分範囲が-∞でなく0から始まるなら-Nではなく0から始める。*/
for(i=-N;i<=N-1;i++){
S += (g(i*dx)+g((i+1)*dx))/2.*dx;
}
printf("計算結果: %e 解析解: %e \n",S,/* 比較のためにここに解析解を書く*/);
return 0;
}
##計算できる例
###例1.
留数定理を使って計算できるような積分
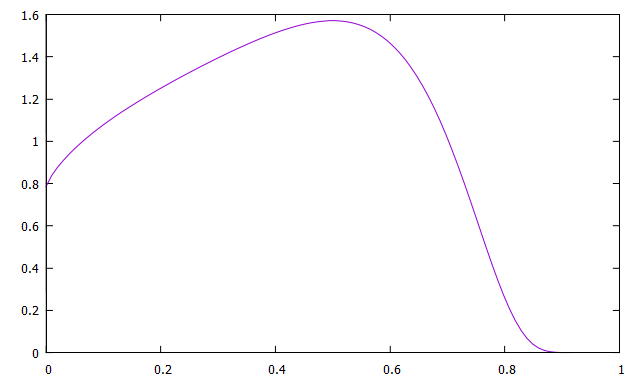
\int_{-\infty}^{\infty}\frac{1}{x^4+1}dx=\frac{\pi}{\sqrt{2}}=2.221441...
計算結果: 2.221441e+000 解析解: 2.221441e+000
被積分関数のプロット(ここでいう被積分関数とは$f(x)$のことでなく、変数変換後の$\frac{\pi}{2\cos^2(\frac{\pi y}{2})}f(\tan(\frac{\pi y}{2}))$のことを指す。以下の例でも同様。)
###例2.
不定積分が解析的に書けないような積分
\int_{0}^{\infty}x^{-x}dx≒1.995456...~~(\rm WolframAlphaより)
計算結果: 1.995456e+000 解析解: 1.995456e+000
被積分関数のプロット
このように不定積分が計算できるが、やはり万能というわけではない。上の2つの関数では[-1:1]で被積分関数が連続でなくなる、または発散するような点をもたないため数値計算ができる。
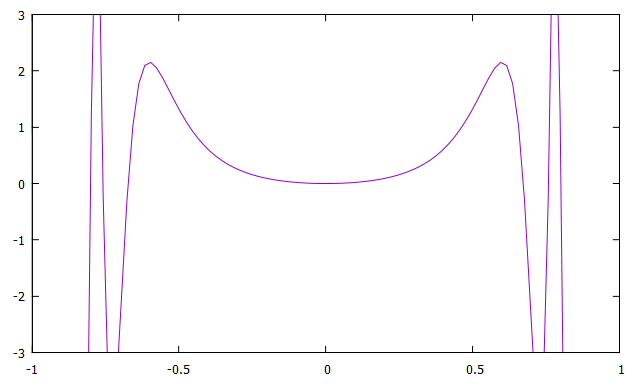
以下の例では被積分関数が[-1:1]で発散するためこのやり方では計算できない。
##計算できない例
###例3.
\int_{0}^{\infty}\frac{\sin(x)}{x}dx=\frac{\pi}{2}=1.570796...~~~(ディリクレ積分)
計算結果: -1.#IND00e+000 解析解: 1.570796e+000
被積分関数のプロット
###例4.
\int_{-\infty}^{\infty}\sin(x^2)dx=\sqrt{\frac{\pi}{2}}=1.253314...~~~(フレネル積分)
計算結果: 7.994463e+027 解析解: 1.253314e+000
被積分関数のプロット
この2つの例では被積分関数が積分区間内で発散するため解析解と数値解の結果のずれが大きくなる。もし、これらの積分を台形公式で計算したいなら$y=\frac{2\arctan(x)}{\pi}$と置換するのではなく別の関数で置換する必要がある。(※自分では思いつかないので、知っている方がいれば教えてください。)