この記事は「データ構造とアルゴリズム Advent Calendar 2019」 5日目の記事です.
あっぶねー
自分の担当明日と勘違いしてた。。。
ぎりぎりセーフということで。
準備しといてよかった。
少し前、「JuliaでGAPを使い、ルービックキューブを解きます。」という記事を書きました。
それが、それなりにウケたので続きみたいなものを書きます。
今回は探索アルゴリズムによって、最適解を求める内容を書きたいと思います。
先に言っておきます
私がルービックキューブの最適解を求めるにはあまりにも時間がなさすぎた。
(許容できる人だけ見てね)
IDA*探索
まずはIDA探索の説明からです。
ダイクストラ法をより一般化したA探索についてはまあ、知っている人も多いかと思います。
簡単に説明するならば、その探索におけるメモリ効率を線形になるようにうまいこと考えたものです。
korfによって、考案されました。
メモリが十分にあるのであれば、A*の方が良いのですが、普通はそんなにあるものでもないですし、
どうしても、メモリを多く使ってしまう問題もしばしばあります。
もう少しだけ詳しく。
IDA starは非常に単純なアルゴリズムで、まずは深さ優先探索で最低限必要な深さまで探索を実行します。
解がみつかればよいですが、みつからなかった場合、探索可能範囲を1段階深くし、1から再探索を行います。
これが、Iterative(再帰的)と呼ばれる所以です。
擬似コードで説明
アルゴリズム自体シンプルなので、擬似コードもとてもシンプルです。
Initilized:
initial_state <- initial state
sum_of_path_cost <- 0 # path-costの和
solution <- empty action list # 最短解の作用列
limit <- infinite: 探索上限 (更新用)
path_cost(parent, child, action) := parent * actionにかかるコスト
is_goal(state) := goal stateならtrue
actions(state) := stateへ作用することのできる作用のすべてを返す
child(parent, action) := parentへactionを作用させた子の状態
heuristic(child) := childから、ゴールまでの評価値
Algorithm IDA star
Function search
Input
state: 現在のIDA starの過程での対象となる状態
path: initial_stateからstateへ至った作用列(LIFO queue)
search_limit: 探索条件:
Output
If IDA star progress find solution then return FOUND,
else it was cutoff then CUTOFF
else NOT FOUND
Begin
# 探索条件を超えたのでCUTOFFを返す
return CUTOFF, if search_limit < sum_of_path_cost + heuristic(state)
# 解をみつけたので、FOUNDを返す
return FOUND, if is_goal(state)
cutoff <- false
For each action ∈ actions(state) do
child = child(state, action)
next for statement, if child in path
# Update path_cost
path_cost = path_cost(state, child, action)
sum_of_path_cost <- sum_of_path_cost + path_cost
path.push(child)
code = search(
state: child
path: path
search_limit: search_limit
)
# 解を見つけることができたら探索終了
return code, if code is FOUND
limit = min(limit, path_cost)
cutoff <- true
path.pop()
sum_of_path_cost <- sum_of_path_cost - path_cost
end for
return code, if cutoff
return NOT FOUND
end
end function
path.push(initial_state)
search_limit <- heuristic(state)
loop
code = search(
state: initial_state
path: path
search_limit: search_limit
)
return solution, if code is FOUND
return CODE -1, if code is NOT FOUND
search_limit <- limit
limit <- infinite
end loop
end algorithm
pattern database
pattern databaseは状態空間の特定の状態を一つ固定し、それを部分ゴールとすることでその状態に到達するまでのコストをheuristic探索へ用いるためのコストテーブルです。
なんだろう、機械学習用語でいったら、学習済みモデルみたいなものだろうか?
うーんなんか違う気もする。
とりあえず、上の2つの部分を決めることとします。
状態空間の状態を一つを固定する
ルービックキューブにおいての部分ゴールを単純に二つ定義します。
- コーナーキューブが揃った状態
- エッジキューブが揃った状態
の二つを部分ゴールとして、このゴールへ到達するのに必要なコストを求めます。
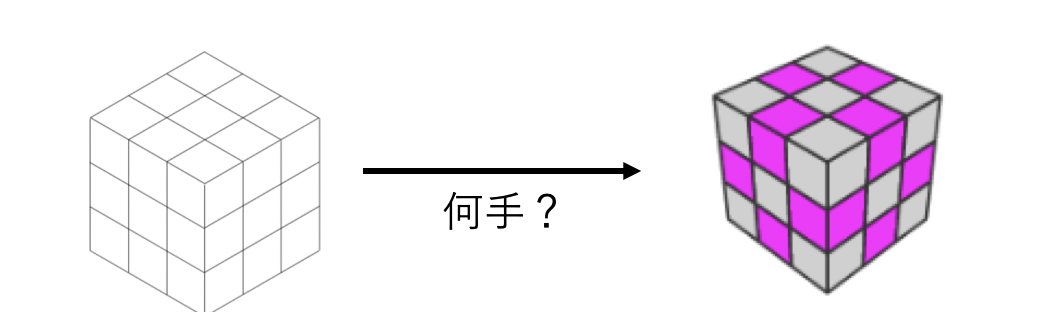
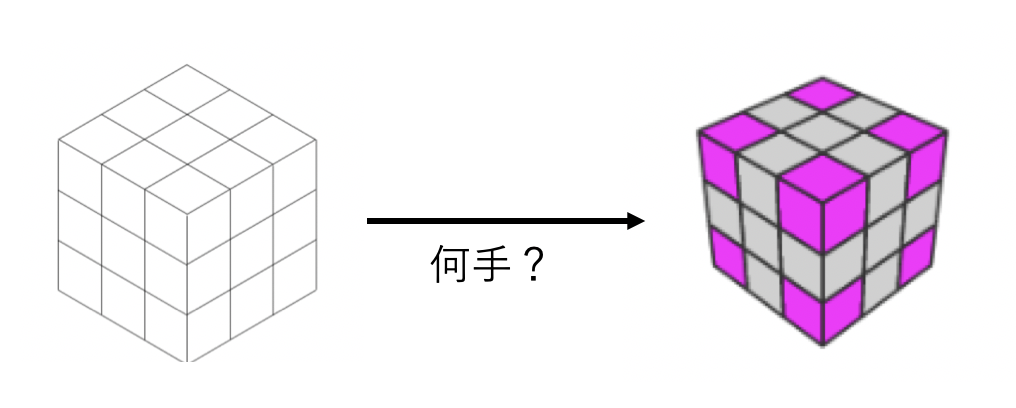
2つの部分的なゴールで、2つのコストの最大値を評価値(heuristic値)として使います。
IDA*を実際に実行してみる
アルゴリズムを実際に実行するために、対象のモデルとして、https://paiza.jp/poh/enshura-special でも紹介された(リンクを開くときは気をつけてください)15Puzzleを試しに使ってみようかとおもいます。
fifteen_puzzle_code(initial_state) = begin
sum_of_path_cost = 0
solution = []
limit = Inf16
path_cost(parent, child, action) = 1
is_goal(state) = begin
for i ∈ 1:15
i ≠ state[i] && return false
end
true
end
actions(state) = begin
list = []
for i ∈ 1:4
for j ∈ 1:4
x, y = i-1, j-1
if state[x * 4 + y + 1] ≠ 16
continue
end
if i ≠ 1
push!(list, ((x - 1) * 4 + y + 1, x * 4 + y + 1))
end
if i ≠ 4
push!(list, ((x + 1) * 4 + y + 1, x * 4 + y + 1))
end
if j ≠ 1
push!(list, (x * 4 + y, x * 4 + y + 1))
end
if j ≠ 4
push!(list, (x * 4 + y + 2, x * 4 + y + 1))
end
end
end
list
end
child(parent, action) = begin
c = Array(parent)
tmp = c[action[1]]
c[action[1]] = c[action[2]]
c[action[2]] = tmp
c
end
heuristic(c) = begin
h = 0
for i ∈ 1:16
c[i] == 16 && continue
x1, y1 = (c[i] - 1) ÷ 4, (c[i] - 1) % 4
x2, y2 = (i - 1) ÷ 4, (i - 1) % 4
h += abs(x1 - x2) + abs(y1 - y2)
end
h
end
function search(state, path, search_limit, search_path)
(search_limit < sum_of_path_cost + heuristic(state)) && return "cutoff" => Array{Tuple{Int64,Int64},1}()
is_goal(state) && return "found" => search_path
cutoff = false
list = actions(state)
for action ∈ list
c = child(state, action)
c ∈ path && continue
push!(search_path, action)
push!(path, c)
cost = path_cost(state, c, action)
sum_of_path_cost += cost
result = search(c, path, search_limit, search_path)
result[1] == "found" && return result
pop!(path)
pop!(search_path)
sum_of_path_cost -= cost
cutoff = true
end
cutoff && return "cutoff" => Array{Tuple{Int64,Int64},1}()
"not found" => Array{Tuple{Int64,Int64},1}()
end
limit = heuristic(initial_state)
search_step = 1
search_path = [initial_state]
for i in 1:100
result = search(initial_state, search_path, limit, Array{Tuple{Int64,Int64},1}())
if result[1] == "found"
println("solution is $(result[2])")
return result[2]
end
if result[1] == "not found"
println("no solution")
return result[2]
end
println("when search step is $(search_step) and limit is $(limit), solution is not found.")
search_step += 1
limit += 1
end
end
上記のコードに対して、例えば
initial_state = [2,7,4,15,13,9,3,8,1,6,16,14,12,5,10,11]
solution = fifteen_puzzle_code(initial_state)
(10, 11),
(9, 10),
(5, 9),
(6, 5),
(10, 6),
(14, 10),
(13, 14),
(9, 13),
(5, 9),
(6, 5),
(7, 6),
(8, 7),
(4, 8),
(3, 4),
(2, 3),
(6, 2),
(10, 6),
(11, 10),
(12, 11),
(8, 12),
(7, 8),
(3, 7),
(2, 3),
(1, 2),
(5, 1),
(6, 5),
(10, 6),
(14, 10),
(15, 14),
(11, 15),
(10, 11),
(14, 10),
(15, 14),
(16, 15),
(12, 16),
(11, 12),
(15, 11),
(16, 15)
の解が出力されます。
もちろん最適解です。
コードはだいぶ適当に書いてるので全然最適化されてませんので。
あれれ、ルービックキューブは?
本当に申し訳ない。
テーブルの作成ができなかった。だから、解くことができなかったんだ。
あれれ、pattern databaseは?
時間もメモリも足りなかった。おそらくこれでいけるだろうというテーブルの作り方だけ載せときます。
# コーナーキューブを定義
Uc = @gap ( 2, 5, 7, 4) * (10,34,26,18);
Lc = @gap (10,13,15,12) * ( 4,20,44,37);
Fc = @gap (18,21,23,20) * ( 7,28,42,13);
Rc = @gap (26,29,31,28) * ( 5,36,45,21);
Bc = @gap (34,37,39,36) * ( 2,12,47,29);
Dc = @gap (42,45,47,44) * (15,23,31,39);
coner_action = [Uc, Uc^2, Uc^3, Lc, Lc^2, Lc^3, Fc, Fc^2, Fc^3, Rc, Rc^2, Rc^3, Bc, Bc^2, Bc^3, Dc, Dc^2, Dc^3]
coner_cube = (@gap Group)(Uc,Lc,Fc,Rc,Bc,Dc)
# エッジキューブの定義
Ue = @gap ( 1, 3, 8, 6) * ( 9,33,25,17) * (11,35,27,19);
Le = @gap ( 9,11,16,14) * ( 1,17,41,40) * ( 6,22,46,35);
Fe = @gap (17,19,24,22) * ( 6,25,43,16) * ( 8,30,41,11);
Re = @gap (25,27,32,30) * ( 3,38,43,19) * ( 8,33,48,24);
Be = @gap (33,35,40,38) * ( 3, 9,46,32) * ( 1,14,48,27);
De = @gap (41,43,48,46) * (14,22,30,38) * (16,24,32,40);
edge_action = [Ue, Ue^2, Ue^3, Le, Le^2, Le^3, Fe, Fe^2, Fe^3, Re, Re^2, Re^3, Be, Be^2, Be^3, De, De^2, De^3]
edge_cube = (@gap Group)(Ue,Le,Fe,Re,Be,De)
function create_table(actions::Array{Main.ForeignGAP.MPtr,1}; search_max = 20)
e = @gap ()
depth_table = [0 => [e], 1 => []] # こいつを保存する
all_set = [e]
depth = 1
current = 1
next = 0
all = 1
while true
s = depth_table[depth][2][current]
current -= 1
for a ∈ actions
ns = s * a
if ns ∉ all_set
push!(depth_table[depth + 1][2], ns)
push!(all_set, ns)
next += 1
all += 1
end
end
if current == 0
println("{ depth: $(depth), created_state: $(next), all_state: $(all) }")
current = next
next = 0
depth += 1
push!(depth_table, depth => [])
end
search_max < depth && return depth_table
end
depth_table
end
# コーナーキューブ
coner_table = create_table(coner_action; search_max=3)
{ depth: 1, created_state: 18, all_state: 19 }
{ depth: 2, created_state: 243, all_state: 262 }
{ depth: 3, created_state: 3240, all_state: 3502 }
# エッジキューブ
edge_table = create_table(edge_action; search_max=3)
{ depth: 1, created_state: 18, all_state: 19 }
{ depth: 2, created_state: 243, all_state: 262 }
{ depth: 3, created_state: 2874, all_state: 3136 }
試しに3つほど実行してみた結果を載せてます。
置換で表現したからかもですねえ。本当は最小完全ハッシュ方などを用いて、テーブルを作成したりとか、もう少し分割を小さくしたりとかしたほうが良いです!
おわりに
今度余裕があれば改良版を載せます。
だいぶ急ぎ足で書いてるのでクソコード書いてます。悪しからず。
やってみた系なんてこんなもんでいいよね。
機械学習も楽しいと思いますが、こういう探索アルゴリズムとかも考えるのは楽しいもんですね!(使い回されたネタですが。。。)
今回のリポジトリ
https://github.com/TsuMakoto/GapjlRubik/blob/master/OptimalSolution.ipynb
リポジトリに15puzzleについての途中経過載せてるので、気になる方はぜひ。