はじめに
これはDMM.com #1 Advent Calendar 2017の2日目の記事です。
新卒1年目が調子に乗ってアドベントカレンダー2日目に立候補してしまいました。後悔はしてません。
今回は17新卒エンジニア見習いが「Octaveで実装する簡単な回帰分析」について書きます。
全て業務外で勉強したことなので、改善点や深くまで理解していない所などあるかもしれませんが暖かい目で読んでもらえるとうれしいです。
経緯
1.8月からタイピングの練習をしていて、毎回wpmを記録していた。
2.11月下旬にCourseraの機械学習コースを始めた。
3.線形回帰を習った。
4.力試しとしてタイピングのグラフを作って線形近似しようと思った
以上です。
分かること
- Octaveを使って線形回帰のグラフをプロットする方法
分からないこと
- 線形回帰の数学的な理論
回帰分析について
今回書くのは統計学における回帰について。
ざっくり書くと、回帰分析とはあるデータの集まりに、Y=f(x)の関数を当てはめることです。
xが1次元なら単回帰、xが2次元以上なら重回帰と言います。
$ Y = \theta_0+\theta_1x_1+\theta_2x_2…\theta_nx_n $というモデルに当てはめたものを線形回帰といいます。
さて、この式ですが、ベクトルで表すと
Y=
\begin{pmatrix}
\theta_0 & \theta_1\;・・・\; \theta_n
\end{pmatrix}
\begin{pmatrix}
x_0 \\ x_1\\︙\\ x_n
\end{pmatrix}\\
=\theta^Tx
になります。
今回は$Y=\theta_0+\theta_1x$という1番簡単な式に当てはめて回帰分析を行います。
 上記のような線を引きます。
上記のような線を引きます。
正規方程式
$Y=\theta_0+\theta_1x$の式に使う$\theta_0$と$\theta_1$を求めるために正規方程式を使用します。
正規方程式とは、線形回帰における$\theta$を求めるための解法の1つです。
詳しくは、わかりやすく説明している記事があるのでこちらを読むと良いと思います。
線形回帰の Normal Equation(正規方程式)について
正規方程式で使用する式は以下です。
なお、$X$は訓練データの入力値、$y$は訓練データの出力値です。
$$\theta=(X^TX)^{-1}X^Ty$$
$X^T$は$X$の転置行列、$X^{-1}$は$X$の逆行列です。
実装
冒頭で述べましたが、今回はOctaveで実装します。
Macならhomebrewでインストールすることが出来ます。
さて、処理の流れとしては、
1.訓練データを読み込む
2.散布図を描く
3.$\theta$を計算する
4.2の散布図に$\theta^Tx$を描く
になります。
訓練データを読み込む
ファイルの読み込みはload([ファイルパス])で出来ます。
今回の訓練データは、Xが日付、yがwpmです。日付はyyyy,mm,ddという形式で保存されているのですが、Octaveはカンマを数の区切りと認識するのでそのまま読み込むと
X=
\begin{pmatrix}
2017 & 8 & 16\\
2017 & 8 & 3\\
︙&︙&︙\\
2017 & 9 & 22
\end{pmatrix}
という風になってしまいます。
これでは$\theta$が計算出来ないので日付はシリアル日付と呼ばれる0000年1月0日を基準とした数値に変換します。
X = datenum(load('date.txt'));
計算する
$$\theta=(X^TX)^{-1}X^Ty$$
この式を使って$\theta$を求めます。
訓練データセットの数が、訓練データの入力値の種類より多い時、下記が成り立ちます。
$$X^{-1} = (X^TX)^{-1}X^T$$
これを使うと、$\theta$は、
$$\theta=X^{−1}y$$
と表せます。
さて、Octaveでは、逆行列をpinvで計算出来るので$\theta$は、以下で求めます。
theta = pinv(X)*y;
描画する
基本的な使い方
Octaveではgnuplotを使って図に点や線をプロットできます。
//基本的なplot() 線が描画される。
plot(X, y);
//青い線を描画
plot( X, y, 'b-');
//点を☓で描画
plot( X, y, 'x');
//マーカーサイズを指定する
plot( X, y,'MarkerSize', 5);
オプションはたくさんあるので公式をみると良いと思います
ホールド
既存の図に重ねて図を描画する場合はhold on;を使います。
plot( X, y, 'b-');
hold on;
plot( a, b, 'x');
X軸に日付を使用する
日付はシリアル日付に変換されているので、図にプロットしたタイミングで元の日付に変換したいと思います。
やり方は簡単です。
図をプロットした後で
datetick(gca);
とすれば軸の目盛りが日付になります。
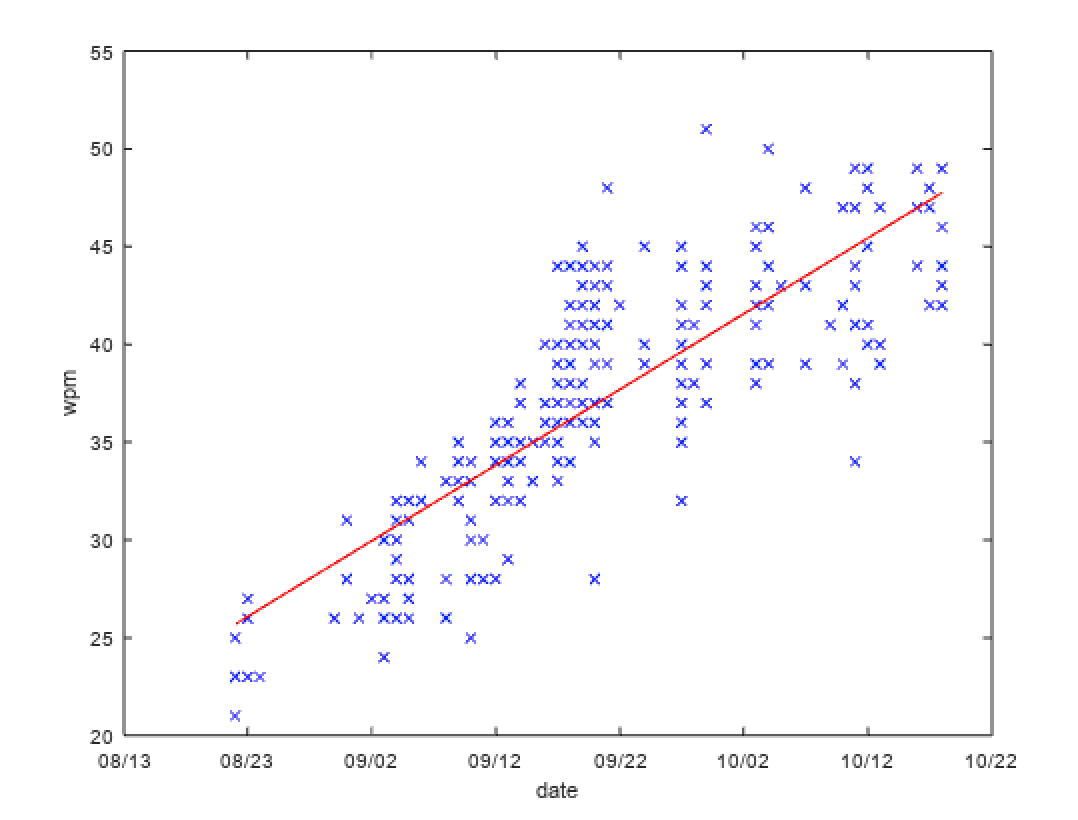
最終的なコード
clear;
X = datenum(load('date.txt'));
y = load('wpm.txt');
m = length(y); % number of training examples
X = [ones(m, 1), X];
theta = pinv(X)*y;
plot( X(:,2), y, 'bx', 'MarkerSize', 5);
hold on;
plot(X(:,2), X*theta, 'r-');
xlabel('date');
ylabel('wpm');
datetick(gca);
ハマった所
**pinv(X'*X)*X'yとpinv(X)yが等しくない
datenum(load('date.txt'))をXに使用したときだけpinv(X'*X)*X'*yとpinv(X)*yが等しくない現象が発生しました。
具体的には、pinv(X'*X)*X'*yがまったく見当違いの値になっていました。
当初はpinv(X'*X)*X'*yを使って計算していたのですが、サンプルの訓練データでは正しくプロット出来ていました。もし同じような現象に出会った方はお気をつけください。