はじめに
この記事はDeNA Advent Calendar 2021の12日目の記事です。
こんにちは。大竹悠人(@Trapezoid)です。
普段はDeNAでモバイルゲームのクライアント基盤開発やゲーム開発で生じる諸々の課題解決を行っています。
今日はUnityのBurst Compilerを用いたC#コードのSIMD化を、ポータブルかつ確実に行う方法論について書こうと思います。
TL;DR
- Burstを用いると簡単にSIMDによる最適化をかけられるが、何も考えないと確実性は低い
- Unity.Mathematicsを利用すると高い可読性、確実性を保ったままSIMD化を狙うことができる
- SIMD最適化をナイーブに行う場合にはデータの並び替え(インターリーブ)が必要になることがあるが、愚直に書くと遅くなることがある
- math.shuffleによってCPU依存の無いポータブルのコードのまま、高効率なインターリーブ用の命令を使わせることができる
Burstについて
BurstはUnityが公式提供している、UnityにおいてハイパフォーマンスなC#スクリプテイングを提供する特殊なコンパイラです。
詳しくはUTJの名雪さん、安原さんによるこちらの講演を見て頂くのが早いと思いますので、詳しい説明はここでは割愛します。
C# Job SystemなNativeContainerとの併用が前提となるという認識がまだ強いかもしれませんが、Burst 1.5からはBurst Direct Callが導入され、Job Systemを使わない普通の関数に対してもBurstCompile属性を付けるだけで適用できるようになり、制約はあるもののNativeContainerではなく(unsafeな)ポインタを用いるようなコードにも適用できるので、格段に導入の敷居は下がっています。
.NETの持つ既存の技術資産の活用や、C#製サーバーとのロジック共有などの運用を考えると、それらが用いることのできるArrray/Spanベースのメモリ表現との接続性の高いポインタでの記述でもBurst化できるのは大きなメリットになります。
なお、Burst Direct Callはメインスレッド以外から呼べないという記述を公式Blog, Forumなどで見かけることがありますが、Burst 1.6系以降ではこの制約は取り払われているため、サブスレッドからも問題なく利用することができます。
(@kawai125 さん指摘ありがとうございます)
BurstによるSIMD化の挙動を確認する
Burstは記述された処理を可能な範囲でベクトル化し、SIMD命令による最適化を行います。
今回の記事の本題だけ書いても誰得な内容になりそうなので、まずはBurstによるSIMD最適化そのものの挙動を確認し、解説してみます。
説明の為、下のような任意のデータ列を簡易的なストリーム暗号にかけて出力するロジックを、xxHashっぽいビット演算を適当に並べて考えてみました。
(あくまで説明の為のサンプルで鍵長も滅茶苦茶に短く、暗号学的な強度は一切考えていないので暗号として実用はしないで下さい)
using Unity.Burst;
namespace Sample
{
[BurstCompile]
public class Normal
{
public static uint Rotate(uint v, int n)
{
unchecked {
return (v << n) | (v >> (32 - n));
}
}
const uint PRIME_1 = 2654435761U;
const uint PRIME_2 = 2246822519U;
const uint PRIME_3 = 3266489917U;
const uint PRIME_4 = 668265263U;
const uint PRIME_5 = 374761393U;
static uint CryptStream(uint i, uint seed)
{
uint result = PRIME_1 * i;
result += seed + PRIME_2;
result = Rotate(result, 17);
result *= PRIME_3;
result ^= result >> 15;
result *= PRIME_4;
result ^= result >> 13;
result *= PRIME_5;
result ^= result >> 16;
return result;
}
unsafe static void Crypt(byte* src, uint offset, uint length, uint seed)
{
//説明のための簡略化として、端数のことは一旦考えない...
//ので、offsetとlengthは4の倍数でないと受け付けない
Crypt((uint*)src, offset / 4,length / 4, seed);
}
[BurstCompile]
unsafe static void Crypt(uint* src, uint offset, uint length, uint seed)
{
//offsetからlengthの区間をuint(4byte)単位で暗号化する
var cryptLength = offset + length;
for(var i = offset; i < cryptLength; i++)
{
//Indexに応じて得られる値とのXORをかけて暗号化。
//iとseedに基づいて決まるので、前後のデータがなくても、途中から復号化できる
src[i] ^= CryptStream(i, seed);
}
}
}
}
これをBurst InspectorでARMV8A_AARCH64向けの出力を確認すると、主要部分は以下のような内容になっています。
; ...省略...
Sample.Normal.Crypt: ; @Sample.Normal.Crypt
; ...省略...
.Ltmp6:
.LBB4_3: ; %vector.body
; =>This Inner Loop Header: Depth=1
;DEBUG_VALUE: cryptLength <- 0
;DEBUG_VALUE: i <- 0
.cv_inline_site_id 3 within 2 inlined_at 1 50 0
=== Normal.cs(23, 1) result += seed + PRIME_2;
mov v16.16b, v0.16b
mla v16.4s, v5.4s, v1.4s
.Ltmp7:
.cv_inline_site_id 4 within 3 inlined_at 1 24 0
=== Normal.cs(10, 1) return (v << n) | (v >> (32 - n));
ushr v17.4s, v16.4s, #15
shl v16.4s, v16.4s, #17
orr v16.16b, v16.16b, v17.16b
.Ltmp8:
=== Normal.cs(25, 1) result *= PRIME_3;
mul v16.4s, v16.4s, v2.4s
=== Normal.cs(26, 1) result ^= result >> 15;
ushr v17.4s, v16.4s, #15
eor v16.16b, v17.16b, v16.16b
.Ltmp9:
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
ldr q7, [x13]
.Ltmp10:
=== Normal.cs(27, 1) result *= PRIME_4;
mul v16.4s, v16.4s, v3.4s
=== Normal.cs(28, 1) result ^= result >> 13;
ushr v17.4s, v16.4s, #13
eor v16.16b, v17.16b, v16.16b
=== Normal.cs(29, 1) result *= PRIME_5;
mul v16.4s, v16.4s, v4.4s
=== Normal.cs(30, 1) result ^= result >> 16;
ushr v17.4s, v16.4s, #16
eor v7.16b, v16.16b, v7.16b
.Ltmp11:
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
eor v7.16b, v7.16b, v17.16b
subs x14, x14, #4 ; =4
str q7, [x13], #16
.Ltmp12:
=== Normal.cs(22, 1) uint result = PRIME_1 * i;
add v5.4s, v5.4s, v6.4s
b.ne .LBB4_3
.Ltmp13:
; %bb.4: ; %middle.block
;DEBUG_VALUE: cryptLength <- 0
;DEBUG_VALUE: i <- 0
=== Normal.cs(46, 1) for(var i = offset; i < cryptLength; i++)
cmp x10, x11
b.eq .LBB4_7
.Ltmp14:
.LBB4_5: ; %BL.0008.i.i.preheader
;DEBUG_VALUE: cryptLength <- 0
;DEBUG_VALUE: i <- 0
mov w15, #34383
movk w15, #25032, lsl #16
sub x9, x9, x12
add x10, x0, x12, lsl #2
mov w11, #44605
mov w13, #60207
mov w14, #26545
msub w8, w12, w15, w8
mov w12, #31153
movk w11, #49842, lsl #16
movk w13, #10196, lsl #16
movk w14, #5718, lsl #16
movk w12, #40503, lsl #16
.Ltmp15:
.LBB4_6: ; %BL.0008.i.i
; =>This Inner Loop Header: Depth=1
;DEBUG_VALUE: cryptLength <- 0
;DEBUG_VALUE: i <- undef
=== Normal.cs(10, 1) return (v << n) | (v >> (32 - n));
ror w16, w8, #15
.Ltmp16:
=== Normal.cs(25, 1) result *= PRIME_3;
mul w16, w16, w11
.Ltmp17:
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
ldr w15, [x10]
.Ltmp18:
=== Normal.cs(26, 1) result ^= result >> 15;
eor w16, w16, w16, lsr #15
=== Normal.cs(27, 1) result *= PRIME_4;
mul w16, w16, w13
=== Normal.cs(28, 1) result ^= result >> 13;
eor w16, w16, w16, lsr #13
=== Normal.cs(29, 1) result *= PRIME_5;
mul w16, w16, w14
=== Normal.cs(30, 1) result ^= result >> 16;
eor w15, w16, w15
.Ltmp19:
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
eor w15, w15, w16, lsr #16
=== Normal.cs(46, 1) for(var i = offset; i < cryptLength; i++)
subs x9, x9, #1 ; =1
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
str w15, [x10], #4
.Ltmp20:
;DEBUG_VALUE: i <- [DW_OP_plus_uconst 1, DW_OP_stack_value] undef
=== Normal.cs(46, 1) for(var i = offset; i < cryptLength; i++)
add w8, w8, w12
b.ne .LBB4_6
.Ltmp21:
.LBB4_7: ; %"Sample.Normal.Sample.Crypt_00000004$BurstDirectCall.Invoke(uint* src, uint offset, uint length, uint seed) -> void_13ac681319c30142cd80c48ee4c7f295.exit"
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
ret
.Ltmp22:
.Lfunc_end4:
.section .xdata,"dr"
.seh_handlerdata
.text
.seh_endproc
; -- End function
; ...省略...
結構長いですね。
.LBB4_3 ラベルから続くコアロジックをざっと見てみると、記述されている命令のoplandの大半に .16b あるいは .4s のsuffixがついているのが確認できます。
=== Normal.cs(23, 1) result += seed + PRIME_2;
mov v16.16b, v0.16b
mla v16.4s, v5.4s, v1.4s
.Ltmp7:
.cv_inline_site_id 4 within 3 inlined_at 1 24 0
=== Normal.cs(10, 1) return (v << n) | (v >> (32 - n));
ushr v17.4s, v16.4s, #15
shl v16.4s, v16.4s, #17
orr v16.16b, v16.16b, v17.16b
これは、8bit * 16 あるいは 32bit * 4、つまり128bitの単位でSIMD命令が使われていることを示しています。
つまりBurstが勝手にSIMDに展開してくれたわけです。そもそも内部的に使っている関数もまるっとインライン化されていることも見て取れます。Burst凄いですよね。
さて、このコードはもともと4byte単位で処理をしているため、SIMDで処理できる16byte単位にできない端数はSIMD以外で処理する必要があります。
このあたりをどうしているのか確認するため、SIMDが適用されている部分の末尾部分を見てみましょう。
subs x14, x14, #4 ; =4
str q7, [x13], #16
.Ltmp12:
=== Normal.cs(22, 1) uint result = PRIME_1 * i;
add v5.4s, v5.4s, v6.4s
b.ne .LBB4_3
.Ltmp13:
; %bb.4: ; %middle.block
;DEBUG_VALUE: cryptLength <- 0
;DEBUG_VALUE: i <- 0
=== Normal.cs(46, 1) for(var i = offset; i < cryptLength; i++)
cmp x10, x11
b.eq .LBB4_7
; ...中略...
.LBB4_7: ; %"Sample.Normal.Sample.Crypt_00000004$BurstDirectCall.Invoke(uint* src, uint offset, uint length, uint seed) -> void_13ac681319c30142cd80c48ee4c7f295.exit"
ret
いくつかの分岐命令が見て取れますが、subsで計算した16byteぶんのカウント(4)を減算し、まだ残りがあれば.LBB4_3まで分岐して引き続きSIMDによる演算を行っています。
その後、端数が無い場合だけ.LBB4_7に分岐してreturnし、そうでなければ(端数があれば)後続の処理を実行しています。
この後続では、SIMDを使わない計算ロジックが記述されています。
.LBB4_6: ; %BL.0008.i.i
; =>This Inner Loop Header: Depth=1
;DEBUG_VALUE: cryptLength <- 0
;DEBUG_VALUE: i <- undef
=== Normal.cs(10, 1) return (v << n) | (v >> (32 - n));
ror w16, w8, #15
.Ltmp16:
=== Normal.cs(25, 1) result *= PRIME_3;
mul w16, w16, w11
.Ltmp17:
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
ldr w15, [x10]
.Ltmp18:
=== Normal.cs(26, 1) result ^= result >> 15;
eor w16, w16, w16, lsr #15
=== Normal.cs(27, 1) result *= PRIME_4;
mul w16, w16, w13
=== Normal.cs(28, 1) result ^= result >> 13;
eor w16, w16, w16, lsr #13
=== Normal.cs(29, 1) result *= PRIME_5;
mul w16, w16, w14
=== Normal.cs(30, 1) result ^= result >> 16;
eor w15, w16, w15
.Ltmp19:
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
eor w15, w15, w16, lsr #16
=== Normal.cs(46, 1) for(var i = offset; i < cryptLength; i++)
subs x9, x9, #1 ; =1
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
str w15, [x10], #4
.Ltmp20:
;DEBUG_VALUE: i <- [DW_OP_plus_uconst 1, DW_OP_stack_value] undef
=== Normal.cs(46, 1) for(var i = offset; i < cryptLength; i++)
add w8, w8, w12
b.ne .LBB4_6
.Ltmp21:
.LBB4_7: ; %"Sample.Normal.Sample.Crypt_00000004$BurstDirectCall.Invoke(uint* src, uint offset, uint length, uint seed) -> void_13ac681319c30142cd80c48ee4c7f295.exit"
=== Normal.cs(50, 1) src[i] ^= CryptStream(i, seed);
ret
ここの末尾ではsubsによって4byteぶんのカウント(1)を減算し、0になるまでこの処理の冒頭の.LBB4_6まで分岐して端数の処理を行っています。
抜粋では省いていますが、関数自体の冒頭で長さが4以下なら初めから端数の計算部のみに分岐するようになっています。
このように、Burstは端数の処理も含め、非常に賢くSIMD化を行ってくれます。
ですが、これは非常に便利であると同時に、SIMD化されるかどうかが大きくBurstの挙動に依存してしまうことを意味しています。
これを示す例として、16byte単位でブロックを構成するストリーム暗号を考えてみます。
using Unity.Burst;
namespace Sample
{
[BurstCompile]
public class LargeState
{
public static uint Rotate(uint v, int n)
{
unchecked {
return (v << n) | (v >> (32 - n));
}
}
const uint PRIME_1 = 2654435761U;
const uint PRIME_2 = 2246822519U;
const uint PRIME_3 = 3266489917U;
const uint PRIME_4 = 668265263U;
const uint PRIME_5 = 374761393U;
struct State
{
public uint Part0;
public uint Part1;
public uint Part2;
public uint Part3;
}
static uint CryptDword(uint i, uint s,
uint prime1, uint prime2, uint prime3, uint prime4, uint prime5)
{
uint result = prime1 * i;
result += s + prime2;
result = Rotate(result, 17);
result *= prime3;
result ^= result >> 15;
result *= prime4;
result ^= result >> 13;
result *= prime5;
result ^= result >> 16;
return result;
}
unsafe static void CryptStream(uint i, State* dest, uint seed)
{
dest->Part0 = CryptDword(i, seed, PRIME_1, PRIME_2, PRIME_3, PRIME_4, PRIME_5);
dest->Part1 = CryptDword(dest->Part0, seed, PRIME_2, PRIME_3, PRIME_4, PRIME_5, PRIME_1);
dest->Part2 = CryptDword(dest->Part1, seed, PRIME_3, PRIME_4, PRIME_5, PRIME_1, PRIME_2);
dest->Part3 = CryptDword(dest->Part2, seed, PRIME_4, PRIME_5, PRIME_1, PRIME_2, PRIME_3);
}
unsafe static void Crypt(byte* src, uint offset, uint length, uint seed)
{
//説明のための簡略化として、端数のことは一旦考えない...
//ので、offsetとlengthは4の倍数でないと受け付けない
Crypt((uint*)src, offset / 4,length / 4, seed);
}
[BurstCompile]
unsafe static void Crypt(uint* src, uint offset, uint length, uint seed)
{
//offsetからlengthの区間をuint(4byte)単位で暗号化する
var cryptLength = offset + length;
State* state = stackalloc State[1];
for(var i = offset; i < cryptLength; i += 4)
{
//Indexに応じて得られる値とのXORをかけて暗号化。
//iとseedに基づいて決まるので、前後のデータがなくても、途中から復号化できる
CryptStream(i, state, seed);
src[i] ^= state->Part0;
src[i + 1] ^= state->Part1;
src[i + 2] ^= state->Part2;
src[i + 3] ^= state->Part3;
}
}
}
}
こちらをBurst Inspectorで確認すると、次のようなSIMDが使われていないことが確認できます。
=== LargeState.cs(11, 1) return (v << n) | (v >> (32 - n));
ror w3, w17, #15
.Ltmp10:
=== LargeState.cs(72, 1) src[i] ^= state->Part0;
mov w4, w1
.Ltmp11:
=== LargeState.cs(35, 1) result *= prime3;
mul w3, w3, w9
.Ltmp12:
=== LargeState.cs(72, 1) src[i] ^= state->Part0;
lsl x4, x4, #2
.Ltmp13:
=== LargeState.cs(36, 1) result ^= result >> 15;
eor w3, w3, w3, lsr #15
;略...
実際には16byteでも状態変数としては非常に小さい例と言えるので、Burstのフロー解析に頼ったSIMD化の成否はアルゴリズムに大きく左右されることが分かります。
書き方次第でSIMD化を誘発することも一定可能ですが、Burstの最適化挙動をかなり把握してコードを書かなければならなくなり、保守上のリスクは大きく増大します。
BurstとUnity.Mathematicsを使った確実なSIMD化
できるだけ確実に、意図的にBurstにSIMD化をさせるには、いくつか方法があります。
例えば、Burst Intrinsicsというものもあります。決まったC#の関数を呼び出すとそのままそれに対応したこれは特定のアーキテクチャの特定の命令に翻訳される、というものです。
Intrinsicsを使うと、完全に狙い通りの命令を使わせることができる一方で、
- 特定のアーキテクチャでしか動作しないため、マルチプラットフォームで動作させるにはそれぞれのアーキテクチャ向けに同じロジックを複数記述する必要が出てくる
- 記述の抽象度も命令に合わせた単位で記述する必要があるため、Intrinsicsで最適化する箇所はアセンブラのようになってしまい、記述性が極めて悪い
- C#のデバッガでデバッグが出来ないので、不具合があったときの修正コストが非常に上がる
などといった問題があります。
このため、今回はこれらを解決できる、Unity.Mathematicsで提供されるベクトル型を使った形でアルゴリズムを記述する手法を紹介します。
この手法では(いかにもSIMDっぽい)ナイーブな記述が必要になりますが、Burstの挙動への依存度が低い形で、狙った通りのSIMD化を実現することが出来ます。
Unity.Mathematicは、Shaderに使うようなものと同様の様々なベクトル型のstructと、それら同士の演算が多数定義されたC#で書かれたライブラリです。
例えば、uint4はuintが4要素(x,y,z,w)あるベクトル型を意味します。例えば単純なuint4同士の加算であれば、以下のように記述します
uint4 result = new uint4(0,1,2,3) + new int4(4,5,6,7)
//result == new uint4(4,6,8,10)
Burstコンパイラはこのベクトル型単位での演算を認識(直接認識してるのではなく、そういうパターンを認識しているような気もしますが)して、コンパイル対象のCPUのSIMD命令を使った演算にほぼそのまま最適化します。
例えばuint4は128bit幅のため、armv8向けではarmv8の128bit幅での32bit整数*4のSIMD命令(.4s系)がそのまま使われることになります。
最適化はBurstコンパイラが行っているだけなので、純粋なC#コードとして動作することももちろん保証されています。(Burstをオフにしても動作します)
つまり、Unity.Mathematicsを使った実装を行うことで、Burst.Intrinsicsなどを使ったCPU依存の記述と異なり、CPUに依存しないポータブルな実装なまま高度なSIMD最適化を狙ってかけることが可能になります。
では、先程のLargeState版をUnity.Mathematicsを使ってSIMD化してみましょう。
using Unity.Burst;
using Unity.Mathematics;
namespace Sample
{
[BurstCompile]
public class Simd
{
public static uint4 Rotate(uint4 v, int n)
{
unchecked {
return (v << n) | (v >> (32 - n));
}
}
static readonly uint4 PRIME_1 = new uint4(2654435761U, 2654435761U,2654435761U, 2654435761U);
static readonly uint4 PRIME_2 = new uint4(2246822519U,2246822519U,2246822519U,2246822519U);
static readonly uint4 PRIME_3 = new uint4(3266489917U,3266489917U,3266489917U,3266489917U);
static readonly uint4 PRIME_4 = new uint4(668265263U,668265263U,668265263U,668265263U);
static readonly uint4 PRIME_5 = new uint4(374761393U,374761393U,374761393U,374761393U);
struct State
{
public uint4 Part0;
public uint4 Part1;
public uint4 Part2;
public uint4 Part3;
}
static uint4 CryptDword(uint4 i, uint4 s,
uint4 prime1, uint4 prime2, uint4 prime3, uint4 prime4, uint4 prime5)
{
uint4 result = prime1 * i;
result += s + prime2;
result = Rotate(result, 17);
result *= prime3;
result ^= result >> 15;
result *= prime4;
result ^= result >> 13;
result *= prime5;
result ^= result >> 16;
return result;
}
unsafe static void CryptStream(uint4 i, State* dest, uint seed)
{
dest->Part0 = CryptDword(i, seed, PRIME_1, PRIME_2, PRIME_3, PRIME_4, PRIME_5);
dest->Part1 = CryptDword(dest->Part0, seed, PRIME_2, PRIME_3, PRIME_4, PRIME_5, PRIME_1);
dest->Part2 = CryptDword(dest->Part1, seed, PRIME_3, PRIME_4, PRIME_5, PRIME_1, PRIME_2);
dest->Part3 = CryptDword(dest->Part2, seed, PRIME_4, PRIME_5, PRIME_1, PRIME_2, PRIME_3);
}
unsafe static void Crypt(byte* src, uint offset, uint length, uint seed)
{
//説明のための簡略化として、端数のことは一旦考えない...
//ので、offsetとlengthは16の倍数でないと動作しない
Crypt((uint4*)src, offset / 16,length / 16, seed);
}
[BurstCompile]
unsafe static void Crypt(uint4* src, uint offset, uint length, uint seed)
{
//offsetからlengthの区間をuint(4byte)単位で暗号化する
var cryptLength = offset + length;
//4要素を一気に計算するために、それぞれの要素のindexを持つようにする
uint4 indexVector = new uint4(0, 4, 8, 12) + offset * 16;
State* state = stackalloc State[1];
for(var i = offset; i < cryptLength; i += 4)
{
//Indexに応じて得られる値とのXORをかけて暗号化。
//iとseedに基づいて決まるので、前後のデータがなくても、途中から復号化できる
CryptStream(indexVector, state, seed);
//XORで暗号化するには、uint4による
//xxxx yyyy zzzz wwwwというメモリ配置ではなく、
//xyzw xyzw xyzw xyzwというメモリ配置にしてかけないと非SIMD版と同一の結果にならない
//これを並び替える必要がある
var xy01 = math.shuffle(
state->Part0, state->Part1,
math.ShuffleComponent.LeftX, math.ShuffleComponent.RightX,
math.ShuffleComponent.LeftY, math.ShuffleComponent.RightY
);
var zw01 = math.shuffle(
state->Part0, state->Part1,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.RightZ,
math.ShuffleComponent.LeftW, math.ShuffleComponent.RightW
);
var xy23 = math.shuffle(
state->Part2, state->Part3,
math.ShuffleComponent.LeftX, math.ShuffleComponent.RightX,
math.ShuffleComponent.LeftY, math.ShuffleComponent.RightY
);
var zw23 = math.shuffle(
state->Part2, state->Part3,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.RightZ,
math.ShuffleComponent.LeftW, math.ShuffleComponent.RightW
);
var x = math.shuffle(
xy01, xy23,
math.ShuffleComponent.LeftX, math.ShuffleComponent.LeftY,
math.ShuffleComponent.RightX, math.ShuffleComponent.RightY
);
var y = math.shuffle(
xy01, xy23,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.LeftW,
math.ShuffleComponent.RightZ, math.ShuffleComponent.RightW
);
var z = math.shuffle(
zw01, zw23,
math.ShuffleComponent.LeftX, math.ShuffleComponent.LeftY,
math.ShuffleComponent.RightX, math.ShuffleComponent.RightY
);
var w = math.shuffle(
zw01, zw23,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.LeftW,
math.ShuffleComponent.RightZ, math.ShuffleComponent.RightW
);
//並び替えられたものとXORをとって暗号化
src[i + 0] ^= x;
src[i + 1] ^= y;
src[i + 2] ^= z;
src[i + 3] ^= w;
indexVector += 16;
}
}
}
}
また大分長くなりました。Burst Inspectorで確認すると、
=== SimdBased.cs(102, 1) result += s + prime2;
mov v19.16b, v5.16b
mla v19.4s, v17.4s, v0.4s
;DEBUG_VALUE: result <- undef
.Ltmp12:
.cv_inline_site_id 5 within 4 inlined_at 1 103 0
=== SimdBased.cs(80, 1) return (v << n) | (v >> (32 - n));
shl v23.4s, v19.4s, #17
ushr v19.4s, v19.4s, #15
orr v19.16b, v23.16b, v19.16b
.Ltmp13:
;DEBUG_VALUE: result <- $q19
=== SimdBased.cs(104, 1) result *= prime3;
mul v19.4s, v19.4s, v2.4s
.Ltmp14:
;DEBUG_VALUE: result <- $q19
=== SimdBased.cs(105, 1) result ^= result >> 15;
ushr v23.4s, v19.4s, #15
eor v19.16b, v23.16b, v19.16b
LargeState版と同様のアルゴリズムでも、SIMD命令が使われていることが確認できました。
このような変数自体をベクタ化してSIMD化する手法は、既存の実装の主要アルゴリズム部分にあまり手を加えずにかなり高い確実性をもってSIMD命令を使わせることが出来ます。
しかし、このような手法を取る際には一つ考慮すべき大きな問題があります。それについて次で説明していきます。
SIMD時のインターリーブの必要性とUnity.Mathematicsによるインターリーブの実装
uint4によってXORするCryptStreamの計算自体をSIMD化することは容易にできますが、その結果を平文/暗号文とXORして用いるときには大きな問題があります。
元のロジックではPart0~3の順に平文とXORをかけるだけでしたが、SIMD版ではuint4として4ブロック分の値が組になってPartNに格納されているため、同じように src[i+N] = state.PartN とすることは出来ません。
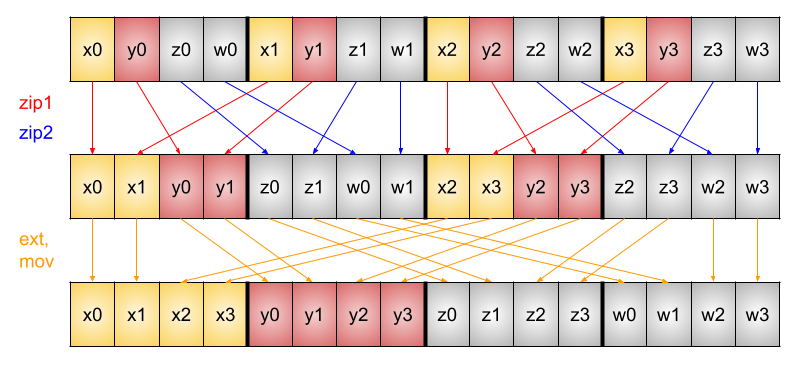
理想的な形に並び替えた後にXORをかける必要があります。図にすると、このような形です。
既存のアルゴリズムをそのままSIMDのレジスタ幅に合わせて並列化するような記述をした場合、このように結果の順序を並び替えなければ後続の処理で利用できないという自体が発生することが偶にあります。
このような並び替え処理はインターリーブ(あるいはインターリーブ解除)などとよく呼ばれるようです。このようなインターリーブに使える命令もSIMDのレジスタ幅で使えるものが用意されていて、armv8a_aarch64にも存在します。
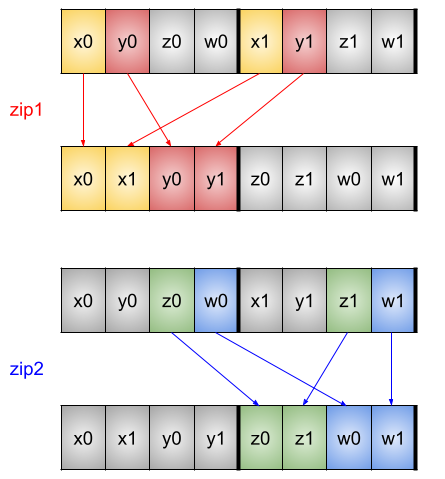
これらのzip命令のほか、特定のビットを境界として上位と下位を抽出する操作を行えるext命令など、並び替えに使える命令は様々なバリエーションがあります。
シンプルにビット操作で実装した場合でもBurstのSIMD化によりこれらの命令が使われることはあるようですが、やはり他と同様にそれに頼るには限界があります。
解決策もまた他と同様で、Unity.Mathematicsを使うことで解決出来ます。
それが、コード例の最後に残った謎のmath.shuffleの連続呼び出しの正体です。
もう一度コードを見てみましょう。
var xy01 = math.shuffle(
state->Part0, state->Part1,
math.ShuffleComponent.LeftX, math.ShuffleComponent.RightX,
math.ShuffleComponent.LeftY, math.ShuffleComponent.RightY
);
var zw01 = math.shuffle(
state->Part0, state->Part1,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.RightZ,
math.ShuffleComponent.LeftW, math.ShuffleComponent.RightW
);
var xy23 = math.shuffle(
state->Part2, state->Part3,
math.ShuffleComponent.LeftX, math.ShuffleComponent.RightX,
math.ShuffleComponent.LeftY, math.ShuffleComponent.RightY
);
var zw23 = math.shuffle(
state->Part2, state->Part3,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.RightZ,
math.ShuffleComponent.LeftW, math.ShuffleComponent.RightW
);
var x = math.shuffle(
xy01, xy23,
math.ShuffleComponent.LeftX, math.ShuffleComponent.LeftY,
math.ShuffleComponent.RightX, math.ShuffleComponent.RightY
);
var y = math.shuffle(
xy01, xy23,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.LeftW,
math.ShuffleComponent.RightZ, math.ShuffleComponent.RightW
);
var z = math.shuffle(
zw01, zw23,
math.ShuffleComponent.LeftX, math.ShuffleComponent.LeftY,
math.ShuffleComponent.RightX, math.ShuffleComponent.RightY
);
var w = math.shuffle(
zw01, zw23,
math.ShuffleComponent.LeftZ, math.ShuffleComponent.LeftW,
math.ShuffleComponent.RightZ, math.ShuffleComponent.RightW
);
//並び替えられたものとXORをとって暗号化
src[i + 0] ^= x;
src[i + 1] ^= y;
src[i + 2] ^= z;
src[i + 3] ^= w;
math.shuffleは呼び出すことで指定した2つのオペランドから任意の要素を任意の順番で抜き出して、新しい値を作るメソッドです。
抜き出す順序はShuffleComponent enumを複数与えることで指定する事が出来ます。
この抜き出しのパターンがzip命令などの128bit幅のレジスタを使える命令で実現可能なものである場合、Burstにそれらの命令を使う形に可能な範囲で最適化を行わせる事ができます。
今回の8回のmath.shuffle呼び出しでは、次のような手順で行っています。
まずzip1/zip2に相当する4byte単位でのインターリーブによって、8byte単位で正しい順になるように並び替えます。
その後、8byte単位での入れ替えを行い、16byte単位での最終的な正しい順に並び替えます。
Burst Inspectorでの内容をmath.shuffle部だけ抜粋すると
=== SimdBased.cs(149, 1) var xy01 = math.shuffle(
zip1 v23.4s, v19.4s, v20.4s
=== SimdBased.cs(159, 1) var xy23 = math.shuffle(
zip1 v25.4s, v21.4s, v22.4s
=== SimdBased.cs(170, 1) var x = math.shuffle(
mov v26.16b, v23.16b
mov v26.d[1], v25.d[0]
=== SimdBased.cs(175, 1) var y = math.shuffle(
ext v25.16b, v25.16b, v23.16b, #8
ext v23.16b, v23.16b, v25.16b, #8
=== SimdBased.cs(154, 1) var zw01 = math.shuffle(
zip2 v19.4s, v19.4s, v20.4s
=== SimdBased.cs(164, 1) var zw23 = math.shuffle(
zip2 v21.4s, v21.4s, v22.4s
=== SimdBased.cs(180, 1) var z = math.shuffle(
mov v23.16b, v19.16b
mov v23.d[1], v21.d[0]
=== SimdBased.cs(185, 1) var w = math.shuffle(
ext v22.16b, v21.16b, v19.16b, #8
ext v19.16b, v19.16b, v22.16b, #8
4byte単位の並び替えは1命令,7バイト単位は2命令で実行できていることが分かります。
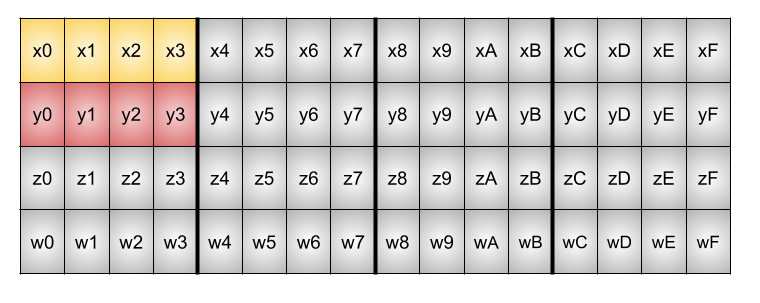
より大きな、64byteで4byte区切りのステートを持つアルゴリズムに適用する場合も、格納先を次のように転置する必要がありますが同じ効率で適用することが可能です。
パフォーマンスの比較
LargeStateとSimdのパフォーマンスをPerformance Test Toolsを使って簡単に計測したところ、Windows PC(Ryzen 9 5900)上では以下のような結果になりました。
| Test Name | Unit | Min | Max | Median | Average | StandardDeviation |
|---|---|---|---|---|---|---|
| PerformanceTest.LargeStatePerformance | Millisecond | 44.6163 | 46.4972 | 44.8606 | 45.1099 | 0.701668482974698 |
| PerformanceTest.SimdPerformance | Millisecond | 17.9977 | 18.1832000000001 | 18.0066999999999 | 18.04182 | 0.0709014922269271 |
Android(armv8_aarch64, Galaxy S9)では以下のような結果になりました。
| Test Name | Unit | Min | Max | Median | Average | StandardDeviation |
|---|---|---|---|---|---|---|
| PerformanceTest.LargeStatePerformance | Millisecond | 141.4706 | 141.9929 | 141.6905 | 141.71916 | 0.171200427569628 |
| PerformanceTest.SimdPerformance | Millisecond | 119.2993 | 119.6151 | 119.3761 | 119.40912 | 0.107766384369166 |
今回の実装によってしっかりパフォーマンスが良くなっていることがわかります。
armv8でのパフォーマンス向上が比率として控えめですが、実際の暗号化実装ではもっとSIMDでゴリッと計算する部分の計算量がかさむため、
実用するときは多くの場合は今回の結果より良好な結果が出るのではないかと思います。
最後に
今回はUnityのBurst Compilerを用いたC#コードのSIMD化を、ポータブルかつ確実に行う方法論について書いてみました。
もはや必須と言っても良い道具にBurstは成長していると思います。とてもプラグマティックな素晴らしいシステムを提供してくれているUnityに感謝します。
DeNAのモバイルゲーム開発の現場でも、パフォーマンスを向上させる手段としてBurstを大いに活用していっています。この記事がUnityでゲーム開発に取り組む皆様の一助になれば幸いです。
DeNAでは今年、2021年度新卒エンジニア・2022年度新卒内定エンジニアの Advent Calendar もあります!
本 Advent Calendar とは違った種類、違った視点での記事をぜひお楽しみください!
▼DeNA 2021年度新卒エンジニア・2022年度新卒内定エンジニアによる Advent Calendar 2021
https://qiita.com/advent-calendar/2021/dena-21x22
また、DeNA 公式 Twitter アカウント DeNAxTechでは、 Blog記事だけでなく様々な登壇の資料や動画も発信してます。是非フォローして頂ければと思います。