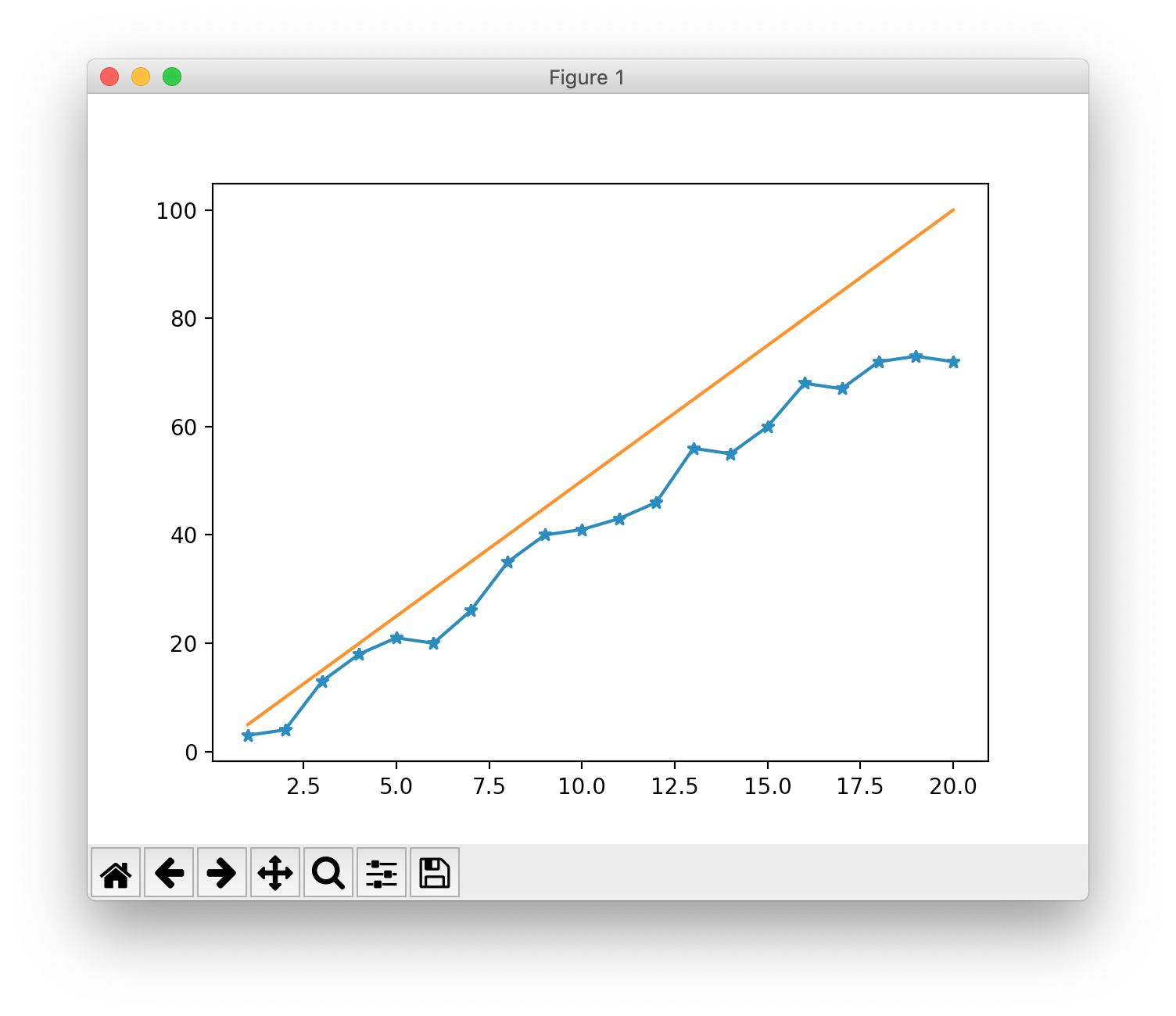
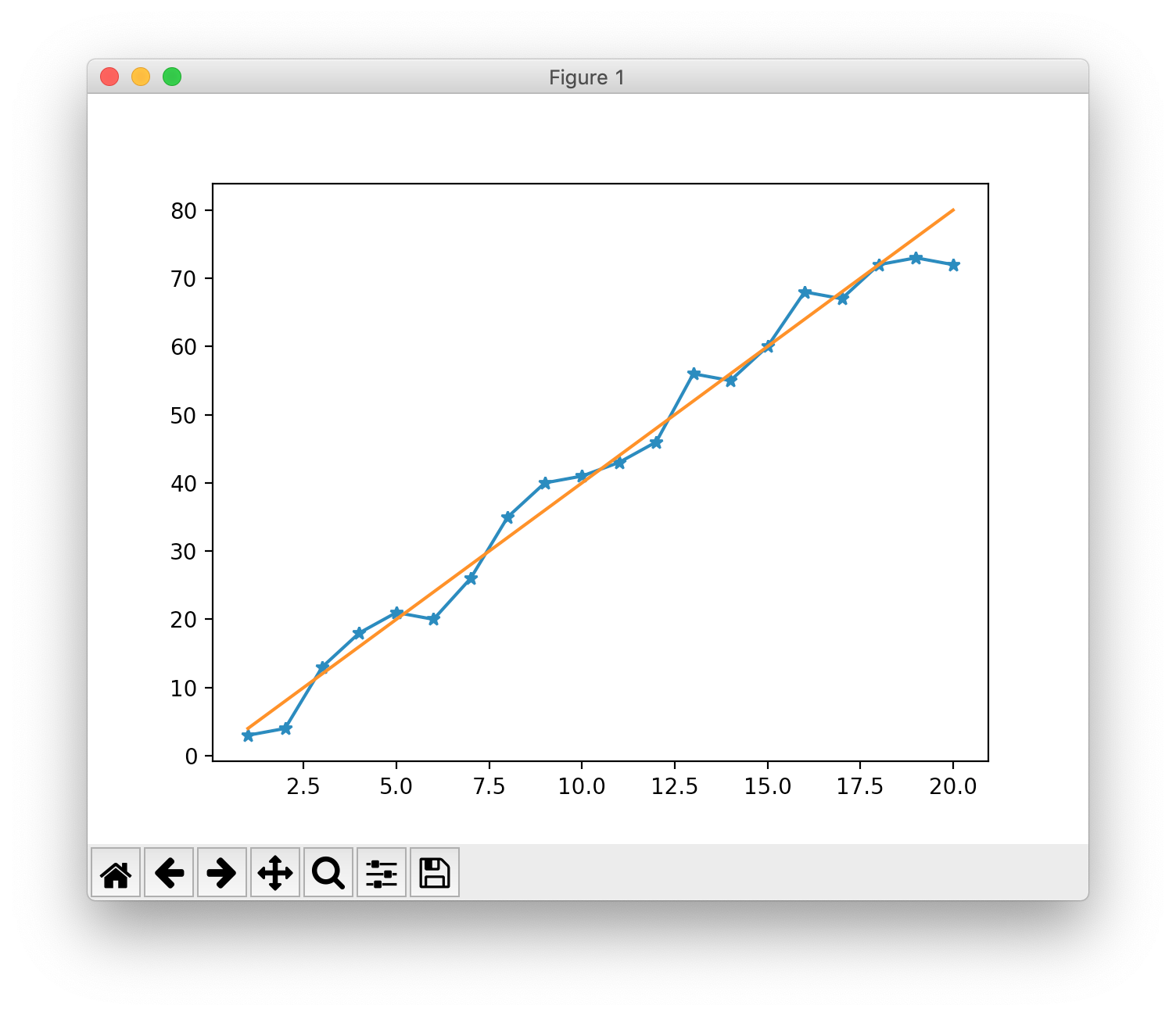
コスト関数とは
どのぐらい学習が正確に駅ているかを判断する指標となる。誤差関数や狭義ではあるが目的関数とも呼ばれる。
アルゴリズムの評価
下図のようなデータを適当に作って、直線で近似することを想定する。
横軸を$x$(入力値)、縦軸を$y$(出力値)とする。
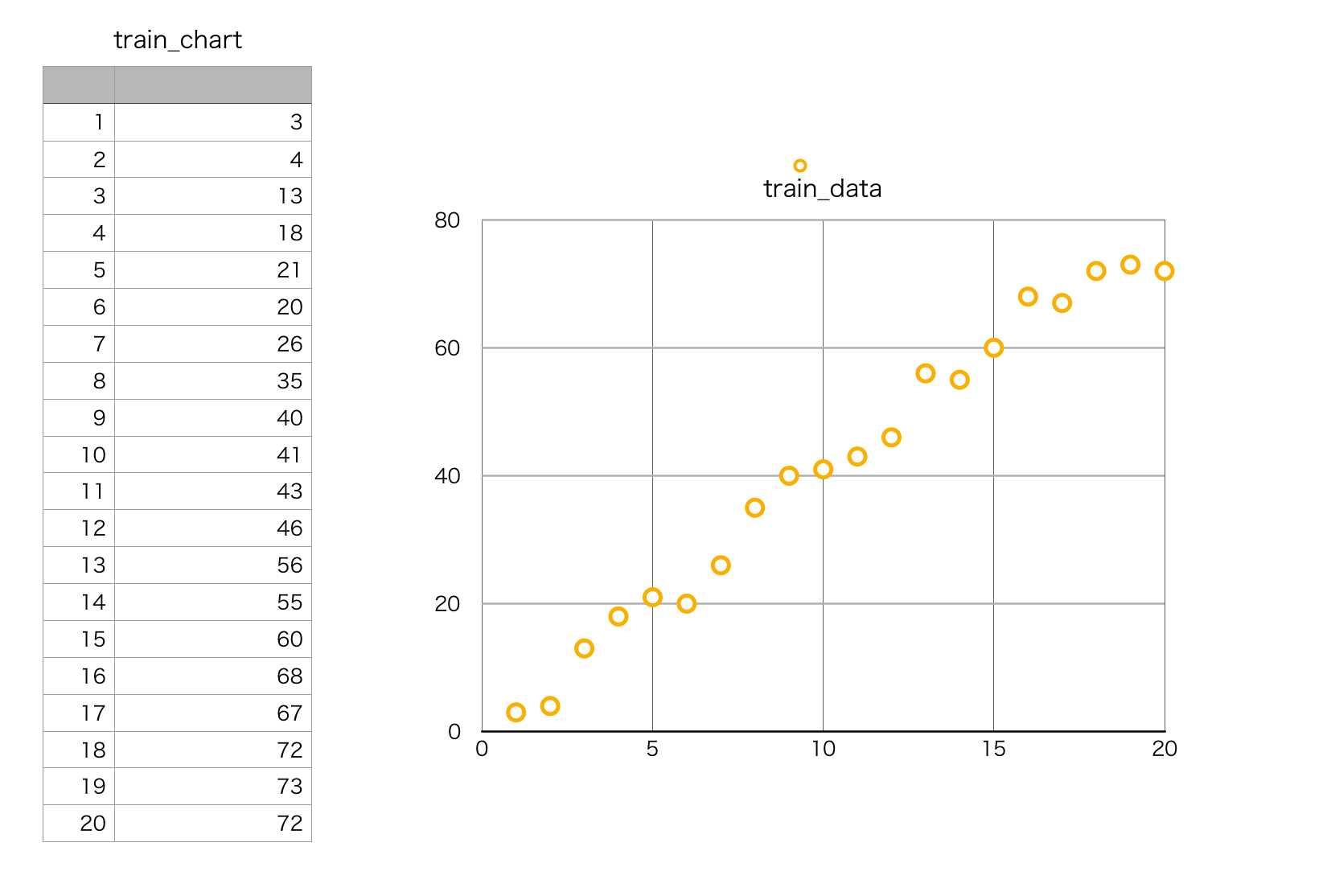
今回はものすごく単純化するためにユニット数1で1層のADALINEで考える。
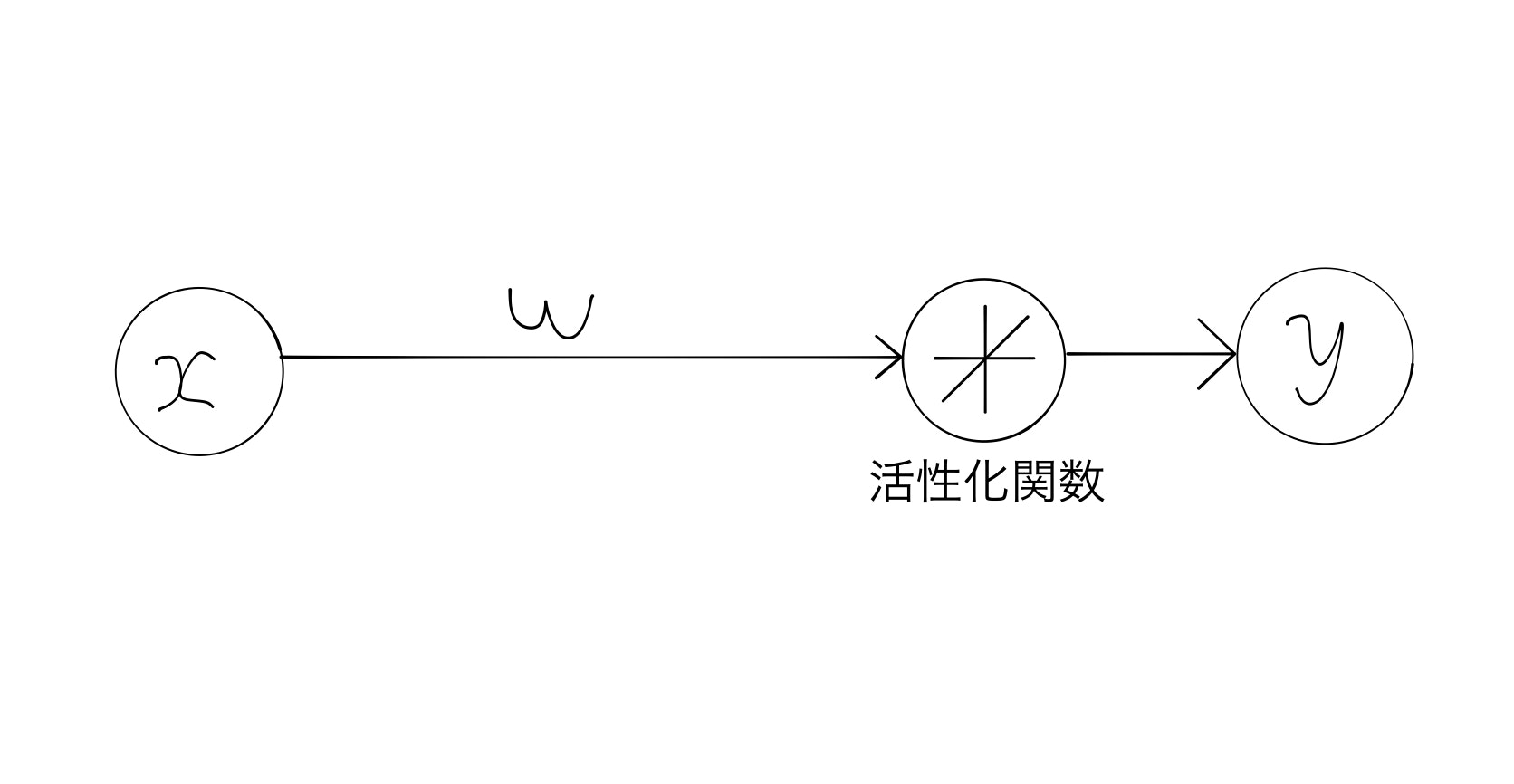
$w$を重み、$x$を入力値とすると、そう総入力関数は
$
f(x) = wx
$
のようにただの実数の積となる(ユニット数1のため)。この$f(x)$とデータの真値$y$を比較すると、
その差(誤差)$d$は次のようになる
$
d = |y - f(x)|
$
最小二乗法をここで用いるためこの誤差$d$を二乗し、またサンプル数$n$だけすべて足すと
$
J(w) = \sum_{i = 0}^{n}(y_n-f(x_n))^2
$
この$J(w)$をコスト関数といい、予測がどれだけ真値に近いかを示すものになる。$w$が変化すると$f(x_n)$が変化するので、**誤差(誤差平方和)**が大きくなったり小さくなったりする。
通常は上の式に$\frac{1}{2}$をかけて
$
J(w) = \frac{1}{2}\sum_{i = 0}^{n}(y_n-f(x_n))^2
$
とすることが多いらしい。
誤差を最小化したい
最終目標はこのコスト関数の値(誤差平方和)を小さくすること
例:w=5のとき
df = pd.read_csv('2.5_test.csv',header=None,names=['x', 'y'])
x = df['x']
y = df['y']
def gosagosa(a,b):
return (a-b)*(a-b)/2
w = 5
fx = w*x
J = 0
for i in range(0,20):
J += gosagosa(fx[i],y[i])
print("w = {0} : J = {1}".format(w,J))
誤差の二乗をすべて足した値Jは
w = 5 : J = 1653.5
となった
wがほかの値のときは?
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('2.5_test.csv',header=None,names=['x', 'y'])
x = df['x']
y = df['y']
#誤差の二乗を計算する関数
def gosagosa(a,b):
return (a-b)*(a-b)/2
# w = 0.0-10.0まで0.1刻みで誤差平方和を計算する
for j in range(0,100):
w = j/10.0
fx = w*x
J = 0
for i in range(0,20):
J += gosagosa(fx[i],y[i])
print("w = {0} : J = {1}".format(w,J))
plt.plot(w,J,marker="+")
plt.show()
誤差の二乗をすべて足した値Jは
w = 0.0 : J = 22538.5
w = 0.1 : J = 21417.65
w = 0.2 : J = 20325.5
w = 0.3 : J = 19262.05
w = 0.4 : J = 18227.3
w = 0.5 : J = 17221.25
...
となり、plotしてみると$w = 4$あたりで最小値となるすることがわかる。つまり今回は重み$w = 4$で最高の精度が現れるということが理解できる。
また、関数は二次曲線を描くため、微分で傾きを求めて最小化の方向へ持っていくことができる。
w = 5
$f(x) = wx$ より、$f(x) = 5x$
ｗ = 4
$f(x) = wx$ より、$f(x) = 4x$
