モンティホール問題をシミュレーションで真面目に検証する

モンティホール問題とは？

アメリカの人気TV番組で行われた3つのドアから当たりを選ぶゲームの事を指します。

このゲームのルール（Wikipediaより）

(1) 3つのドア (A, B, C) に（景品、ヤギ、ヤギ）がランダムに入っている。
(2) プレーヤーはドアを1つ選ぶ。
(3) モンティは残りのドアのうち1つを必ず開ける。
(4) モンティの開けるドアは、必ずヤギの入っているドアである。
(5) モンティはプレーヤーにドアを選びなおしてよいと必ず言う。

プレーヤーはドアを選びなおすべきでしょうか？？？

大論争

答えは「YES」です。
なぜならば、ドアを変更した場合、当たる確率が2倍になるためです。
しかし、普通に考えれば、
「結局のところ、残された2枚のドアのうち、当たりがあるのはどちらかなので
当たる確率は1/2である。」となるのではないか？
実際に、アメリカで大論争を巻き起こした問題です。

この問題のポイント

　この問題のポイントはルールのうち(3)と(4)であり、これにより事前確率と事後確率が変わります。
　つまり、ルール(4)によりドアを変更した場合の方が変更しない場合よりも、当たる確率が2倍となります。

Pythonによるシミュレーション

シミュレーション実装の基本方針

Python3.Xにて実装

1.ドアの枚数を最低3枚、最大枚数はコンソールから入力出来る様にする。

2.各ドア枚数毎の試行回数についても、コンソールから入力出来る様にする。

3.当たりのドアについては乱数で決定する。

4.プレーヤーが最初に選択するドアについても乱数で決定する。

5.ドアの選択を最初のままにするか、変えるか、各場合について当たる確率を計算する

6.最後に各ドア枚数毎の結果を表示する。

コード

MontyHallProblemSimulator3_v2.py

import math
import time
import os
import glob
import numpy as np
import random
import tqdm
from tqdm import trange
import matplotlib.pyplot as plt

##################### Function Definition #####################

def DisplayMessage():

    print("")
    print("******************************************************")
    print("*******           Monty Hall Problem           *******")
    print("******************************************************")
    print("")

    print("Simulation Start")
    print("")

def DecideWinningDoor(nn):

    global win
    win = random.randint(0,nn)
    #print '%d' % (win)
    #print u"当たりのドア %d 番目！" % (win)
    #print('当たりのドア {0} 番目!'.format(win))


def SelectDoor(nn):

    global sel
    sel = random.randint(0,nn)
    #print '%d' % (sel)
    #print u"選んだドア %d 番目！" % (sel)
    #print('選んだドア {0} 番目!'.format(sel))

def DispResult():

    plt.title('Monty Hall Problem Simulator',fontsize=15)
    plt.xlabel("Door Num",fontsize=15)
    plt.xlim([MinDoorNum-1,MaxDoorNum])
    plt.ylabel("Result",fontsize=15)
    plt.ylim([0,100.0])
    plt.scatter(xx, y1, marker="o",alpha=0.5,color='red')
    plt.scatter(xx, y2, marker="o",alpha=0.5,color='blue')
    plt.plot(xx, y1, label = "Door CHANGE", color = "red")
    plt.plot(xx, y2, label = "NO CHANGE", color = "blue")
    plt.legend(["NO Change","Door Changed"], loc="best")
    plt.grid(True)
    plt.show()

#################################################################
    
# if __name__ == '__main__':
    
### Program Start ###
xx = []
ap_x = xx.append
y1 = []
ap_y1 = y1.append
y2 = []
ap_y2 = y2.append

win1 = 0
win2 = 0
DisplayMessage()

MaxDoorNum = int(input('MAX Door Num ===> '))
print('最大ドア数 = {0} 枚'.format(MaxDoorNum))

trial = int(input('Trial Num ===> '))
print('試行回数 = {0} 回'.format(trial))

# trial = 5000

MinDoorNum = 3
# MaxDoorNum = 30

pbar = tqdm(total=(MaxDoorNum+1)-MinDoorNum)

for nn in range(MinDoorNum,MaxDoorNum+1,1):
    win1=0
    win2=0
    for i in range(trial):

        door = [0]*nn

        DecideWinningDoor(nn-1)
        SelectDoor(nn-1)
        #ドアを変更しない場合
        if sel == win:
            win1 = win1 + 1
            #print("変更せずに商品GET!!!")
        #ドアを変更した場合
        if sel != win:
            win2 = win2 + 1
            #print("変更して商品GET!!!") 
  
    ap_x(nn)
    ap_y1(win1*100/trial)
    ap_y2(win2*100/trial)
    pbar.update(1)

####### 結果の表示 #######
DispResult()

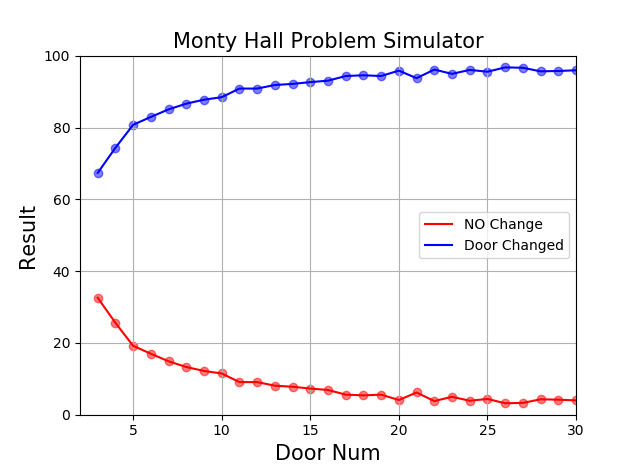
結果

予想通り、ドア枚数が3枚の時にはドアを変更した時の方が変更しない場合の2倍の確率で当たりになりました。

ドア枚数が増えると、ドアを変更した時の方が格段に当たる確率が高くなっていくことが分かります。

【シミュレーション条件】

ドア枚数：3枚～30枚
各試行回数：1000回

試行回数を大きくするに従ってシミュレーション精度が高くなっていきます（当たり前ですが^^;)