はじめに
状態遷移テストを行うときにUMLツール1を用いたモデルを作成することは多いと思います。しかし、UMLツールでモデルを書いて「状態遷移テストをやろう」となったときに、UMLの記法が原因で上手くテスト設計できない場合があります。
前提
本記事では状態遷移図は"受理状態集合を持たないDFA2"とします。DFAについてはWikipediaの記事などを参照してください。
直交合成状態
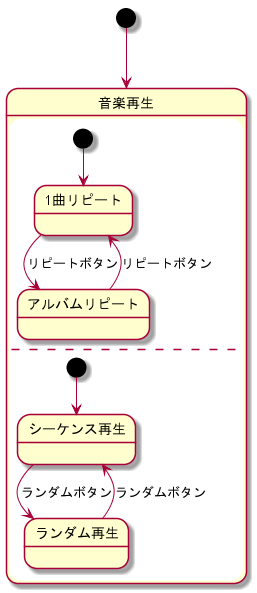
音楽プレーヤーの音楽再生状態として、以下のような直交合成状態を持つステートマシン図を例とします。
困りどころ
端的にいうと「状態が複数の領域に分かれていて、各領域に状態遷移図がある」モデルです。各領域は並行に動作することを表します。個人的には独立(各領域の挙動が他領域に影響しない)ことを期待しますが、一般的にはどうなんでしょう?
直交合成状態を持つステートマシン図を用いて状態遷移テストを行うときにぶつかるだろう問題点は「各領域の状態遷移テストは作成できるが、複数の領域をどのように扱えば良いかは分からない」ことだと想定します。
例えば音楽再生のリピート領域の0スイッチカバレッジを満たすテストケースは以下のとおりです。
| 遷移元状態 | イベント | 遷移先状態 |
|---|---|---|
| 1曲リピート | リピートボタン | アルバムリピート |
| アルバムリピート | リピートボタン | 1曲リピート |
同様に、音楽再生のランダム領域の0スイッチカバレッジを満たすテストケースは以下のとおりです。
| 遷移元状態 | イベント | 遷移先状態 |
|---|---|---|
| シーケンス再生 | ランダムボタン | ランダム再生 |
| ランダム再生 | ランダムボタン | シーケンス再生 |
では、音楽再生状態において、0スイッチカバレッジを満たすテストケースはどのように作れば良いでしょうか。複数ある領域の扱い方が難しいと思います。また、例では規模が小さいため何とかなりそうですが、規模が大きくなったり、0よりも大きいNスイッチカバレッジを扱う場合などは尚更扱いが難しくなります。
状態遷移テストをつくる方針
同時に動作する複数のDFAと、等価になる1つのDFAを作成する方法4があります。今回扱う状態遷移図はほとんどDFAなので、同様の方法を用います。
- 各領域の状態の組合せをつくる
- 初期状態を決める
- イベントをつなぐ
- 状態内状態遷移図の内外をつなぐ
- テストケースをつくる
1. 各領域の状態の組合せをつくる
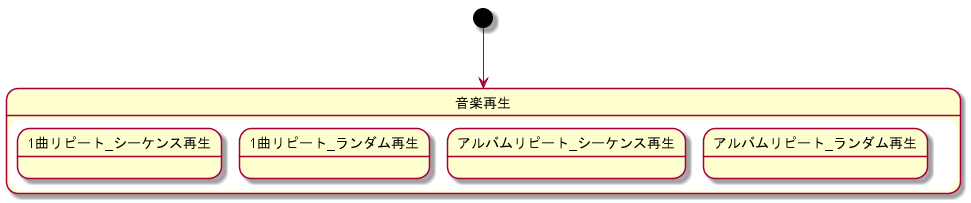
各領域の状態のすべての組の集合を作成します。例の場合、リピート領域に2状態、ランダム領域に2状態なので、2x2=4状態となります。
各領域の状態の組合せは以下のとおりです。
| シーケンス再生 | ランダム再生 | |
|---|---|---|
| 1曲リピート | (1曲リピート,シーケンス再生) | (1曲リピート,ランダム再生) |
| アルバムリピート | (アルバムリピート,シーケンス再生) | (アルバムリピート,ランダム再生) |
作成過程の状態遷移図は以下のとおりです。
2. 初期状態を決める
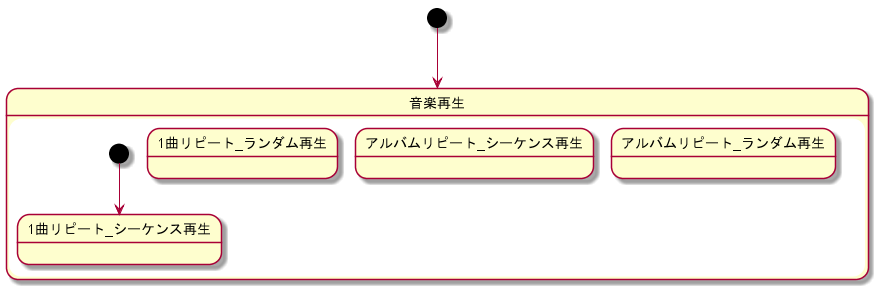
作成中の状態遷移図における初期状態、各領域の初期状態の組になります。各初期状態の表は以下のとおりです。
| 対象 | 初期状態 |
|---|---|
| リピート領域 | 1曲リピート |
| ランダム領域 | シーケンス再生 |
| 作成中の状態遷移図 | (1曲リピート,シーケンス再生) |
初期状態を考慮した作成中の状態遷移図は以下のとおりです。
3. イベントをつなぐ
各領域で現れたすべてのイベントに対して遷移を表す矢印をつないでください。各領域が独立していた場合を想定します。
例えば、手順1で作成した状態に対する、リピート領域で現れたイベントの遷移関数表は以下のとおりです。
ただし、*はワイルドカードとし、遷移元状態における*の具体値と遷移先状態における*の具体値は等しくなるものとします。
| 遷移元状態 | イベント | 遷移先状態 |
|---|---|---|
| (1曲リピート,*) | リピートボタン | (アルバムリピート,*) |
| (アルバムリピート,*) | リピートボタン | (1曲リピート,*) |
同様に、ランダム領域に現れたイベントの遷移関数表は以下のとおりです。
| 遷移元状態 | イベント | 遷移先状態 |
|---|---|---|
| (*,シーケンス再生) | ランダムボタン | (*,ランダム再生) |
| (*,ランダム再生) | ランダムボタン | (*,シーケンス再生) |
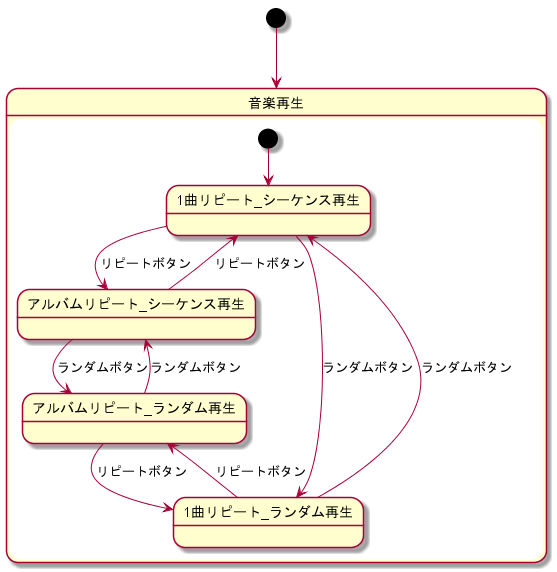
遷移関数表を元に作成した状態遷移図は以下のとおりです。
状態遷移表は以下のとおりです。
| 初期状態 | 状態番号 | 遷移元状態 | リピートボタン | ランダムボタン |
|---|---|---|---|---|
| 〇 | 1 | (1曲リピート,シーケンス再生) | 2 | 3 |
| 2 | (アルバムリピート,シーケンス再生) | 1 | 4 | |
| 3 | (1曲リピート,ランダム再生) | 4 | 1 | |
| 4 | (アルバムリピート,ランダム再生) | 3 | 2 |
4. 状態内状態遷移図の内外をつなぐ
「状態の中にある状態遷移図」を展開します。手順1~3では、音楽再生状態の中にある複数の領域を1つの領域に変換しました。
全体の初期状態は音楽再生状態を指しています。音楽再生状態の初期状態は(1曲リピート_シーケンス再生)です。そのため、遷移先が音楽再生状態である遷移について、遷移先を(1曲リピート,シーケンス再生)に差し替えます。
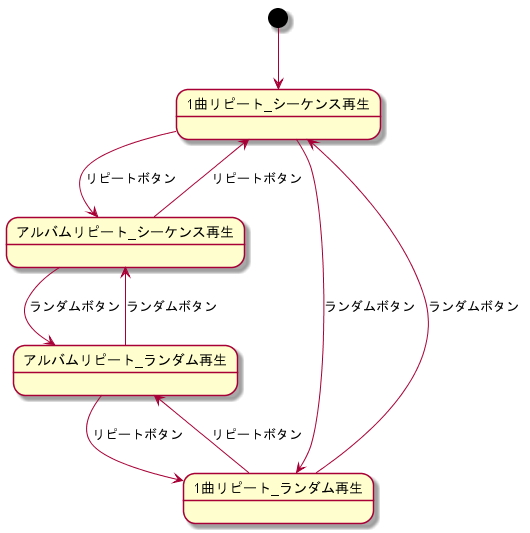
音楽再生状態を展開した状態遷移図は以下のとおりです。
状態遷移表は手順3と変わらないため省略します。
5. テストケースをつくる
完成した状態遷移図は以下のとおりです。(手順4と同様)
完成した状態遷移表は以下のとおりです。(手順3と同様)
| 初期状態 | 状態番号 | 遷移元状態 | リピートボタン | ランダムボタン |
|---|---|---|---|---|
| 〇 | 1 | (1曲リピート,シーケンス再生) | 2 | 3 |
| 2 | (アルバムリピート,シーケンス再生) | 1 | 4 | |
| 3 | (1曲リピート,ランダム再生) | 4 | 1 | |
| 4 | (アルバムリピート,ランダム再生) | 3 | 2 |
状態遷移図と状態遷移表を元に作成した0スイッチカバレッジを満たすテストケースは以下のとおりです。
| 遷移元状態 | イベント | 遷移先状態 |
|---|---|---|
| (1曲リピート,シーケンス再生) | リピートボタン | (アルバムリピート,シーケンス再生) |
| (1曲リピート,シーケンス再生) | ランダムボタン | (1曲リピート,ランダム再生) |
| (アルバムリピート,シーケンス再生) | リピートボタン | (1曲リピート,シーケンス再生) |
| (アルバムリピート,シーケンス再生) | ランダムボタン | (アルバムリピート,ランダム再生) |
| (1曲リピート,ランダム再生) | リピートボタン | (アルバムリピート,ランダム再生) |
| (1曲リピート,ランダム再生) | ランダムボタン | (1曲リピート,シーケンス再生) |
| (アルバムリピート,ランダム再生) | リピートボタン | (1曲リピート,ランダム再生) |
| (アルバムリピート,ランダム再生) | ランダムボタン | (アルバムリピート,シーケンス再生) |
直交合成状態のあとがき
直交合成状態を持つステートマシン図と、直交合成状態を展開した状態遷移図を比較したときに、状態遷移図が直感に反して複雑だと感じた人もいるのではないでしょうか。直交合成状態は並行に動作する状態遷移図を分解することができ、シンプルな実装を行うために有用な考え方だと思います。
ただし、状態遷移テストを行うときには、ステートマシン図のシンプルさに対して多くのテストケースが必要になる場合があります。
ガード条件
まだ
履歴状態
まだ
-
Astah*, Enterprise Architect, PlantUMLなど
今回はUMLの記法で書かれたモデル(以下、ステートマシン図)を状態遷移テストで利用できるように変換する方法をまとめたいと思います。 ↩ -
Deterministic finite automaton (決定性有限オートマトン)
UMLにおける状態遷移図相当はステートマシン図と呼ばれています。本記事では、ガードや履歴状態といったUML特有の記法を含むものをステートマシン図、含まないものを状態遷移図として区別します。3 ↩ -
本記事での定義であり、一般的な定義かどうかは分かりません。 ↩
-
今回用いる方法はProduct Constructionといいます。
直交合成状態を1つの状態遷移にすることで、一般的な状態遷移テストを適用できるようにします。5 ↩ -
手順1~3がProduct Constructionに相当します。 ↩