OpenCV-Pythonで画像処理 ～二値化～

1. はじめに

最近OpenCVでの画像処理を始めるようになったので、
勉強したことを覚書として、残していきたいと思っています。

2. 画像作成

今回わかりやすいように0~255にグラデーションする参考画像を作成しました。

import cv2
import numpy as np

# グラデーション画像を作成
img = np.arange(256,dtype='uint8').reshape(1,-1)
for i in range(255):
	img = np.append(img, np.arange(256, dtype='uint8').reshape(1,-1), axis=0)

# 画像を保存
cv2.imwrite('grad.png', img)

3. 単純な閾値処理

単純な敷居処理として、OpenCVでは以下の関数が用意されています。

ret, dst = cv2.threshold(src, threshold, max_value, threshold_type)

返り値	内容
ret	適用された閾値
dst	二値化された画像

引数	内容
src	入力画像
threshold	閾値
max_value	閾値以上の値がとる値
threshold_type	使用する二値化手法

threshold_typeには、以下の5種類があります。

二値化処理のタイプ	閾値より大きい	閾値より小さい
cv2.THRESH_BINARY	最大値（第３引数）	0
cv2.THRESH_BINARY_INV	0	最大値（第３引数）
cv2.THRESH_TRUNC	閾値（第２引数）	値は入力のまま
cv2.THRESH_TOZERO	値は入力のまま	0
cv2.THRESH_TOZERO_INV	0	値は入力のまま

上記画像の生成コード

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('grad.png',0)

ret,thresh1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
ret,thresh2 = cv2.threshold(img,127,255,cv2.THRESH_BINARY_INV)
ret,thresh3 = cv2.threshold(img,127,255,cv2.THRESH_TRUNC)
ret,thresh4 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO)
ret,thresh5 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO_INV)

titles = ['Original Image','BINARY','BINARY_INV','TRUNC','TOZERO','TOZERO_INV']
images = [img, thresh1, thresh2, thresh3, thresh4, thresh5]

for i in range(6):
    plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
    plt.title(titles[i])
    plt.xticks([]),plt.yticks([])

plt.show()

4. 大津の二値化

#3では手動で閾値を決めていましたが、画像によって適切な閾値を決める1つのやり方に、大津の二値化というものがあります。

第4引数にcv2.THRESH_OTSUを入れることで実行できます。

import cv2
import numpy as np

img = cv2.imread('grad.png',0)

ret,dst = cv2.threshold(img, 0, 255, cv2.THRESH_OTSU)

cv2.imshow('dst', dst)

cv2.waitKey(0)
cv2.destroyAllWindows()

4-1. 詳細

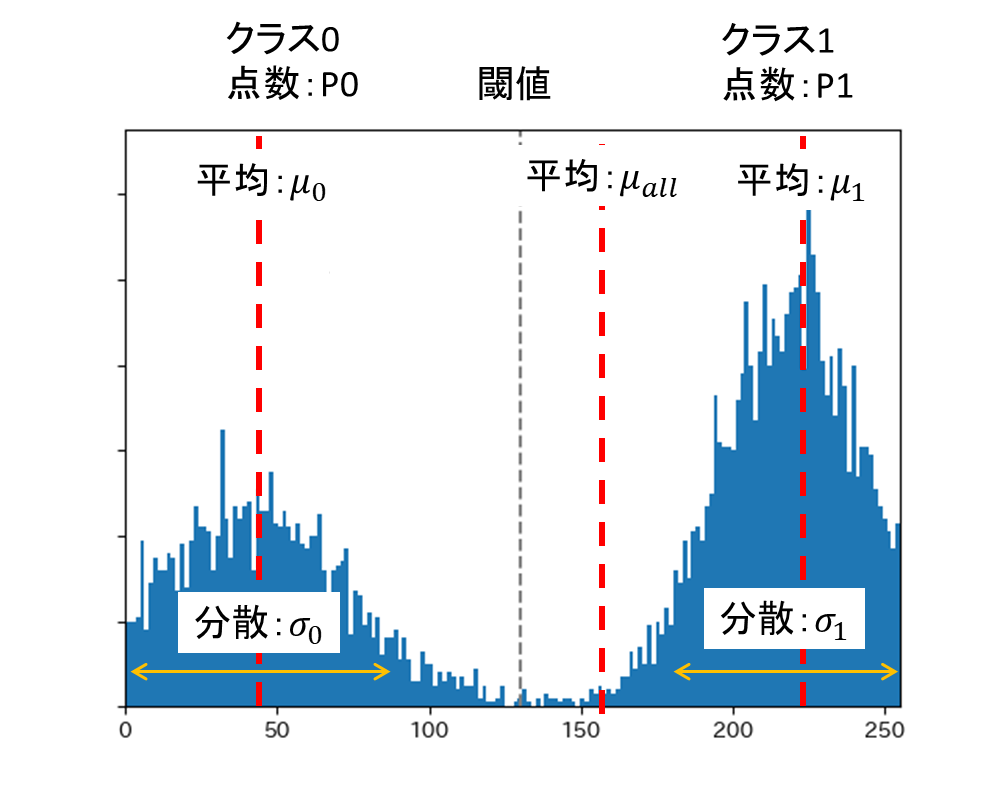
全体の画素数$P_{all}$とし、閾値以下のものをクラス0、以上のものをクラス1とする。
クラス0に含まれる画素数$P_{0}$,、クラス1に含まれる画素数$P_{1}$とすると、全体におけるクラス0の割合$R_0$と全体におけるクラス1の割合$R_1$は

R_{0}=\frac{P_0}{P_{all}} ~~ , ~~ R_{1}=\frac{P_1}{P_{all}} 

になります。

全ての画素の輝度($0\sim 255$)の平均を$\mu_{all}$、クラス0内の平均を$\mu_{0}$,、クラス1内の平均を$\mu_{1}$とした時、クラス0とクラス1のクラス間分散$S_{b}^2$は以下のように定義されています.

\begin{array}{ccl}
S_b^2 &=& R_0\times (\mu_0 - \mu_{all})^2 ~ + ~ R_1\times (\mu_1 - \mu_{all})^2 \\
&=& R_0\times (\mu_0 - (\frac{\mu_0\times P_0 + \mu_1\times P_1}{P_0 + P_1}))^2 ~ + ~ R_1\times (\mu_1 - (\frac{\mu_0\times P_0 + \mu_1\times P_1}{P_0 + P_1}))^2 　\\
&=& R_0 \times R_1 \times (\mu_0 - \mu_1)^2
\end{array}

またクラス0内の分散を$S_0^2$、クラス1の分散を$S_1^2$とすると、各クラスごとの分散をもとにした全体のクラス内分散$S_{in}^2$は以下のように定義されています。

S_{in}^2 = R_0 \times S_0^2 ~ + ~ R_1 \times S_1^2

ここで全体の分散$S_{all}=S_b^2 + S_{in}^2$を考えると、全体の分散は閾値$t$に依らない値なので、ここでは定数と考えることができます。なので分離度$X$を変形して、

X=\frac{S_b^2}{S_{in}^2}=\frac{S_b^2}{S^2 - S_b^2}

とすると、分離度$X$を最大化するには、全体の分散$S$は定数なので「$S_b^2$を大きくすれば良い」ということが分かります。

つまり最適な閾値$t$は

S_b^2 = R_0 \times R_1 \times (M0 - M1)^2

が最も大きくなるようなものであることになります。

なので大津の二値化では$0\sim 255$のすべてを閾値に選んだ時、最も$S_b^2$が大きくなる数値を適切な閾値として選択するようになっています。

5. 適応的二値化処理

全体を見て、部分的に光の当たり方が違う際等は、局所的に適切な閾値を設定するほうが、明確な結果を得られる場合があります。

dst = cv2.adaptiveThreshold(src, maxValue, adaptiveMethod, thresholdType, blockSize, C)

返り値	内容
dst	二値化された画像

引数	内容
src	入力画像
maxValue	閾値以上の値がとる値
adaptiveMethod	閾値の種類
blockSize	閾値計算に利用する近傍領域サイズ
C	計算した閾値からCを引いた値を最終的な閾値にする

adaptiveMethodには以下の2つがあります。

二値化処理のタイプ	内容
cv2.ADAPTIVE_THRESH_MEAN_C	近傍画素値の平均値
cv2.ADAPTIVE_THRESH_GAUSSIAN_C	ガウシアンの重み付き平均値

また、blockSizeは近傍領域の1辺のサイズで、奇数で設定する必要があります。
blockSize = 3であれば、3X3の8近傍が対象となります。

以下の写真をブロックサイズを変えて二値化していこうと思います。適応的二値化はこのように部位によって明るさが異なるような例に使用するとよいとされています。

下は上記画像をそれぞれブロックサイズを変えて二値化した例です。ブロックサイズが小さいほど(block size is 3)、周辺の輝度の差に敏感に反応するため、ノイズのようなドットが出てきます。逆にブロックサイズが大きいと(block size is 255)左側が全体的に黒くなってしまい、物体の輪郭が読み取れません。この例ですと、block sizeが31や63の際がよいと考えられます。

上記画像の生成コード

import cv2
from matplotlib import pyplot as plt

img = cv2.imread('cat.png',0)

area = [3,15,31,63,127,255]

for i in range(6):
    plt.subplot(2,3,i+1)
    new_img =  cv2.adaptiveThreshold(img, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY,area[i],0)
    plt.imshow(new_img,'gray')
    plt.title("block size is {}".format(area[i]))
    plt.xticks([]),plt.yticks([])

plt.show()

6. まとめ

画像処理の基礎的なところですが、考え始めると色々と奥が深いなと感じました。