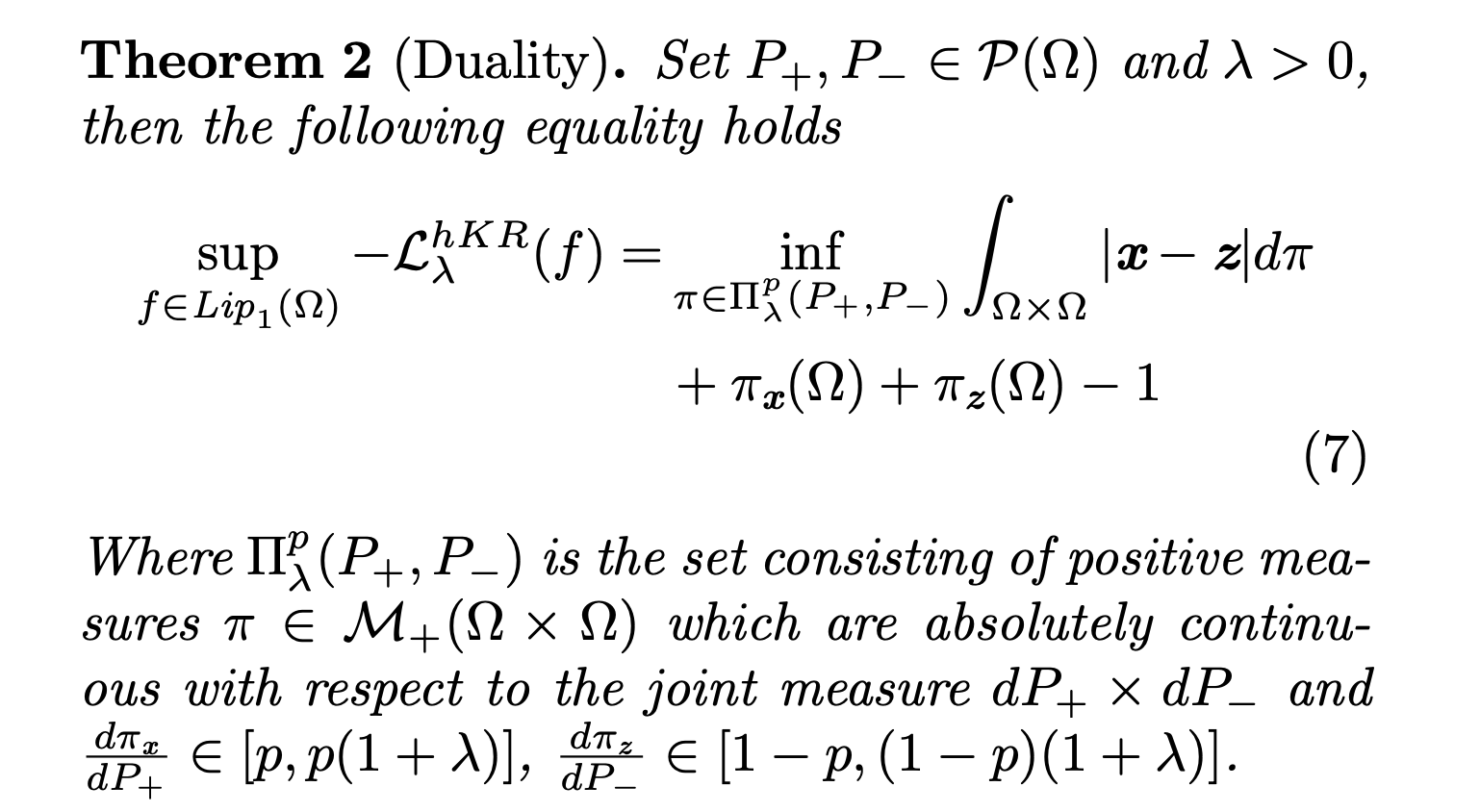論文↓
Achieving robustness in classification using optimal transport with hinge regularization
そもそもNeural Networkのロバスト性ってなに?
これまでの研究から、Neural Networkには敵対的画像(adversarial example)が存在することが知られています。
敵対的画像とは、Neural Networkの入力に対して、NNが誤分類をするようにノイズを加えた画像のことです。例えばめっちゃ精度を出すNeural Networkであっても、うまく攻撃を防御するように学習していないと簡単に敵対的画像を生成されてしまいます。
Neural Networkのロバスト性とは、敵対的画像が入力されても正しく分類できる性質です。近年の流れから、新しい攻撃手法は、既存のロバストなNeural Networkやロバストになる学習方法で学習されたneural Networkに対して攻撃を仕掛けて、ロバスト性を低下させることを目標に開発されています。
敵対的画像は、例えば自動運転の分野であったり、防犯カメラで人物検知 をする際に大きな問題となります。そのため、2014年以降、この敵対的画像を生成する攻撃手法と攻撃を防ぐ防御手法が開発されており、現在に至っても絶対的な防御手法や攻撃手法の開発はできていません。
有名な事例で、自動で交通標識を認識するシステムを搭載した自動車が、天下一品のロゴを交通標識の侵入禁止のマークと誤認識した事例がありました。
先行研究では
先行研究では、1-Lipschitz性をNeural Networkの制約として加えるとロバスト性が向上することが知られていました。しかし、これまでの制約のかけ方では、1-Lipschitz性を重視するあまり、本来のタスクの精度が低下することが課題となっていました。
そこで本手法では、1-Lipschitz性を担保しつつ、精度を向上させる防御手法を提案しました。以下で、手法の詳細について述べ、最後に実験結果を示します。
※1-Lipschitz性についてはappendixに定義を記載しています。
Wasserstein距離(Earth Mover Distance, EM Distance)の導出
Wasserstein距離とは、2つの確率分布が与えられたときの近さを表すものです。画像処理や音声処理では比較的有名な距離尺度として情報科学の分野で知られています[1]。
距離空間$\Omega$上の2つの確率分布$\mu, \nu$におけるEM distanceは、
$$\displaystyle W(\mu, \nu) = \inf_{\pi \in \Pi}(\mu, \nu)\mathbb{E}_{x,z\sim \pi}||\bf x-\bf z||$$
です。ここで、$\Pi(\mu, \nu)$は$\mu$と$\nu$を周辺分布とする$\Omega\times \Omega$上の確率測度全体です。
特にwasserstein-1距離では、Kantorovich-Rubinsteinの双対表現が知られています。
W(\mu,\nu)=\sup_{f\in Lip_1(\Omega)}\mathbb{E}_{x\in \mu}[f(\mathbf{x})]-\mathbb{E}_{x\in\nu}[f(\mathbf{x})]
ここで$Lip_1(\Omega)$とは、 $\Omega$上の1-Lipschitzな関数全体を表しています。
EM distanceを用いているものとして、例えばWasserstein GANはその双対表現をcritic(他のGANにおけるDiscriminator、生成画像か実画像かどうかを2値分類する分類器)の目的関数として学習しています。Wasserstein距離を今回のrobust trainingに対して用いる理由は、NNにLipschitz正則化を与える必要があり、既存の研究から、学習済みのNNがロバストなることが期待されているためです。
まず、単純にkantorovich-Rubinsteinの双対表現を用いて2値分類を行う分類器を学習させた場合にうまくいかない例を示し、本論文でのmain contributionであるhinge-KRロスについて示していきます。
KR classifierの導出
KR classifierの導出$X$を特徴ベクトル空間として、2値分類問題を考えます。ラベル集合を$Y={1,-1}$とします。また2つの確率分布$P_+=\mathbb{P}(X|Y=1)$、$P_- = \mathbb{P}(X|Y=-1)$を用意し、確率変数$Y$に関する事前分布として、$p=P(Y=1)$を設定します。
この定義により、$1-p=P(Y=-1)$となります。この2値分類問題は、$p=\frac{1}{2}$の場合に安定します。
Wasserstein GANのcriticの学習と同様にして、$P_+$と$P_-$を分類する学習済み分類器を$f^* $とする。このとき次で定まる$f^*_c$の符号(Sign)を見れば分類が可能となる
f^*_c(x)=f^*(x)-\frac{1}{2}(\mathbb{E}_{z\sim P_+}[f^*(z)]+\mathbb{E}_{z\sim P_\_ }[f^*(z)])
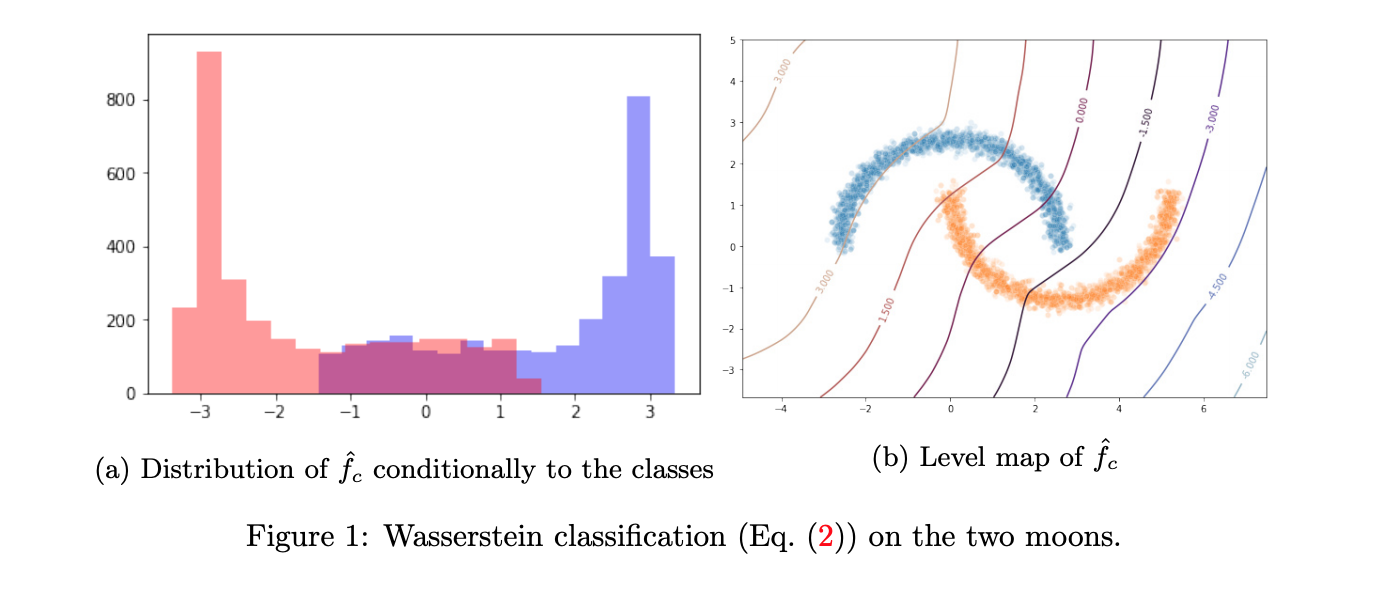
上記のFig1は、KR classificationのトイデータに対する分類結果である。$\hat{f}$は、実験的に得られた解(大域的最適解とは限らない)を表している。(a)(b)からわかるように、うまく分類できていない。筆者らは、kantorovich-Rubinsteinの双対表現で学習された分類器について、2つの分布における画像の期待値の差分を最大化することでは、2つの分布の重なりを最小化(=うまく分類すること)を達成していないと要因分析をしている。
Hinge-KRの導出Hinge lossについて
上記のうまく分類できない問題に対して、著者らはHinge Lossを追加して対応しています。Hinge Loss自体は、最近GANの学習において着目を浴びており、代表的なものとして、SPADE3と呼ばれる手法があります4。
著者らは、Hinge Lossを先程のkantorovich-Rubinsteinの双対表現に加えた損失関数として
\sup_{f\in Lip_1(\Omega)} -L_\lambda^{hKR}(f)=\inf _{f\in Lip_1(\Omega)}\mathbb{E}_{x \sim P_\_}[f(x)]-\mathbb{E}_{x\sim P_+}[f(x)]+\lambda \mathbb{E}_x(1-Yf(x))_+
を提案しており、この損失関数をHinge-KR lossと提唱しています。Hinge Lossは最後の項です。Neural Networkが正しく分類しているときにロスが$0$となり、逆に正しく分類できていないとロスが発生するようになっています。
実際、$Y=1\ (-1)$の場合、NNの出力が$f(x)=1 \ (-1)$だとロスが0になり、$f(x)=-1 (1)$の場合、ロスが$2$になります。
さらに、著者は、Hinge-KR lossで学習した場合、
- 最適解が存在していること(Theorem 1)
- 最適輸送理論の1つであるとみなせること(Theorem 2)
を示しています。
Hinge-KR lossを用いた場合のadversarial example
Hinge-KR lossを用いて学習された学習済みモデル$f$について、ある画像$x$に対するadversarial example $adv(f,x)$は、
$$\displaystyle
adv(f,x)=\underset{z\in \Omega|sign(f(z))=-sign(f(x))}{\arg\min} ||x-z||$$
と表される。制約$sign(f(z))=-sign(f(x))$で誤分類していることを表しており、最小化する対象である$||x-z||$で加えられているノイズが最小となることを表しています。
ここで、Hinge-KR lossで学習された分類器$f$は、1-Lipschitzである(そのように学習する)ことから次の不等式が成り立ちます。
$$|\hat{f}(x)|\leq |\hat{f}(x)-\hat{f}(adv(\hat{f},x))|\leq ||x-adv(\hat{f}, x)||.$$
この不等式により、任意のadversarial attackのノイズの最小ノルムが$|\hat{f}(x)|$であることがわかります。
よって、Hinge-KR lossで学習された学習済みモデルは、
- Hinge Lossにより精度が向上する
- KR Lossによりロバスト性向上する
ことが期待されます。
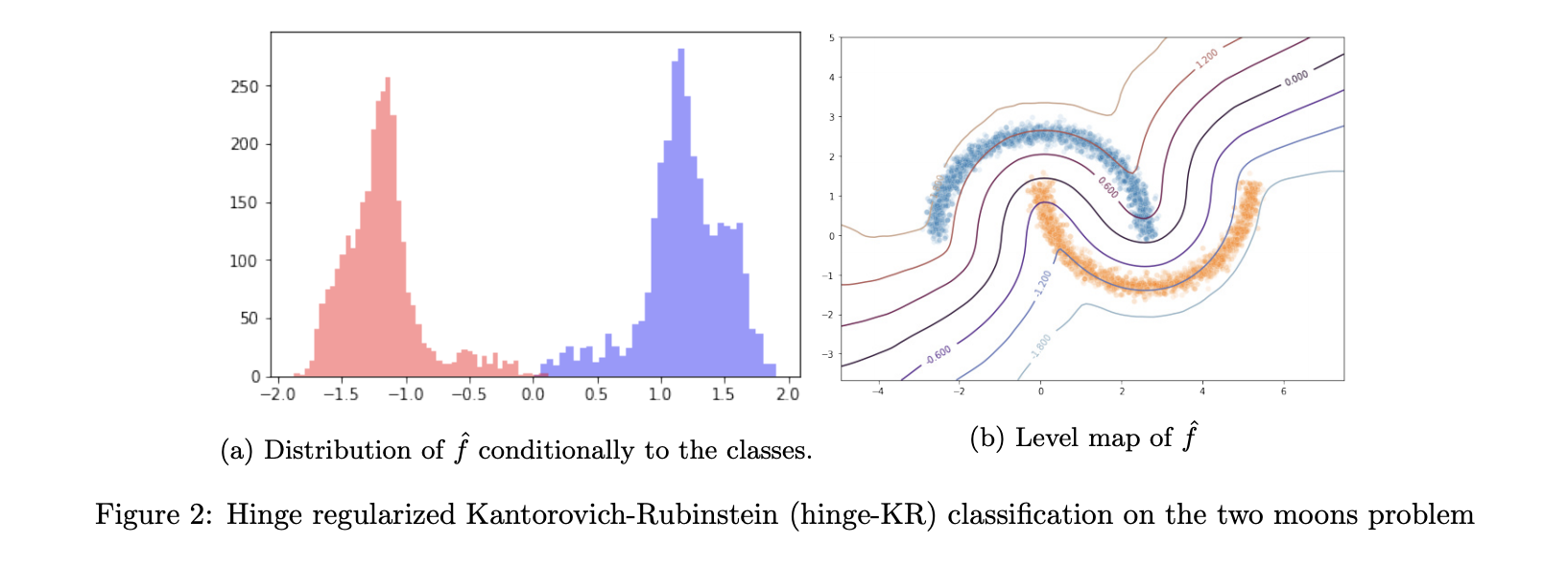
上記のFig2は、Hinge-KR lossを用いて、トイデータに対して学習を行なった結果です。Fig1と比較して、(a)で精度が向上していることがわかります。
複数クラスへの対応
これまでは2値分類を対象に考えてきたが、CIFAR10に代表されるデータセットではマルチクラスに対応していることが必要である。著者らは上記のHinge-KR lossで学習するNNをクラス数分用意して、one-vs-allで学習・推論をさせれば良いとしています。
これでマルチクラスのデータセットへの適用が可能となり、既存の手法との比較が可能となりました。
どうやって有効だと検証した?
著者らは、5つの手法と比較しています。
- $Adv$: Adversarial learning[6]
- $LIP_{log}$: [7]で提唱されている方法に従って学習。
- $GNP_{hin}^m$ : hinge lossに関する勾配の正則化を行なって学習[8]。
- $GNP_{log}$: [8]の類似で、log entropy lossに関する勾配の正則化を行なって学習。
- $hKR_\alpha^m$ : 提案手法。
使用データセットは以下の3つである。
- MNIST: one-hotクラス分類
- CIFAR10:one-hotクラス分類
- Celeba-A:バイナリクラス分類
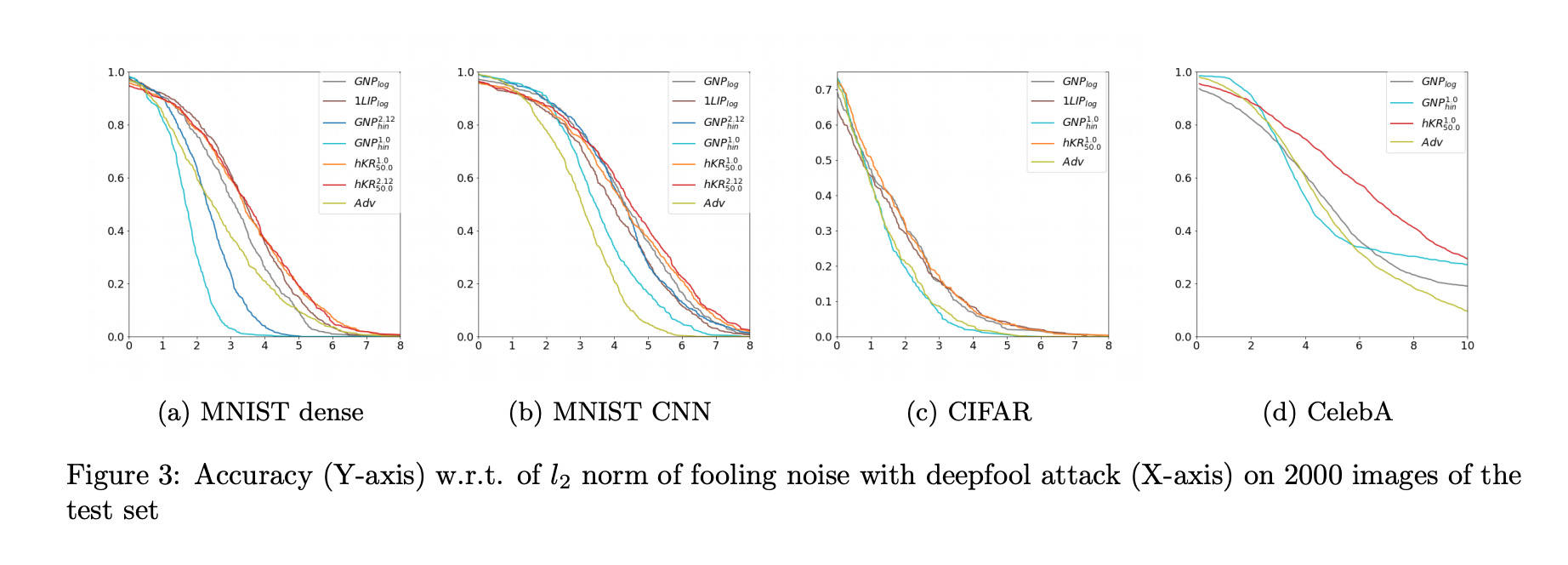
上記のFig3は、5つの手法で学習したモデルに対して、deepfool[9]という攻撃手法を適用し、画像枚数が増える(横軸)ごとに、攻撃を受けて正解率(縦軸)が減少していく様子を可視化しています。これを見ますと、提案手法であるhKRの正解率の減少傾向が緩やかであることがわかります。
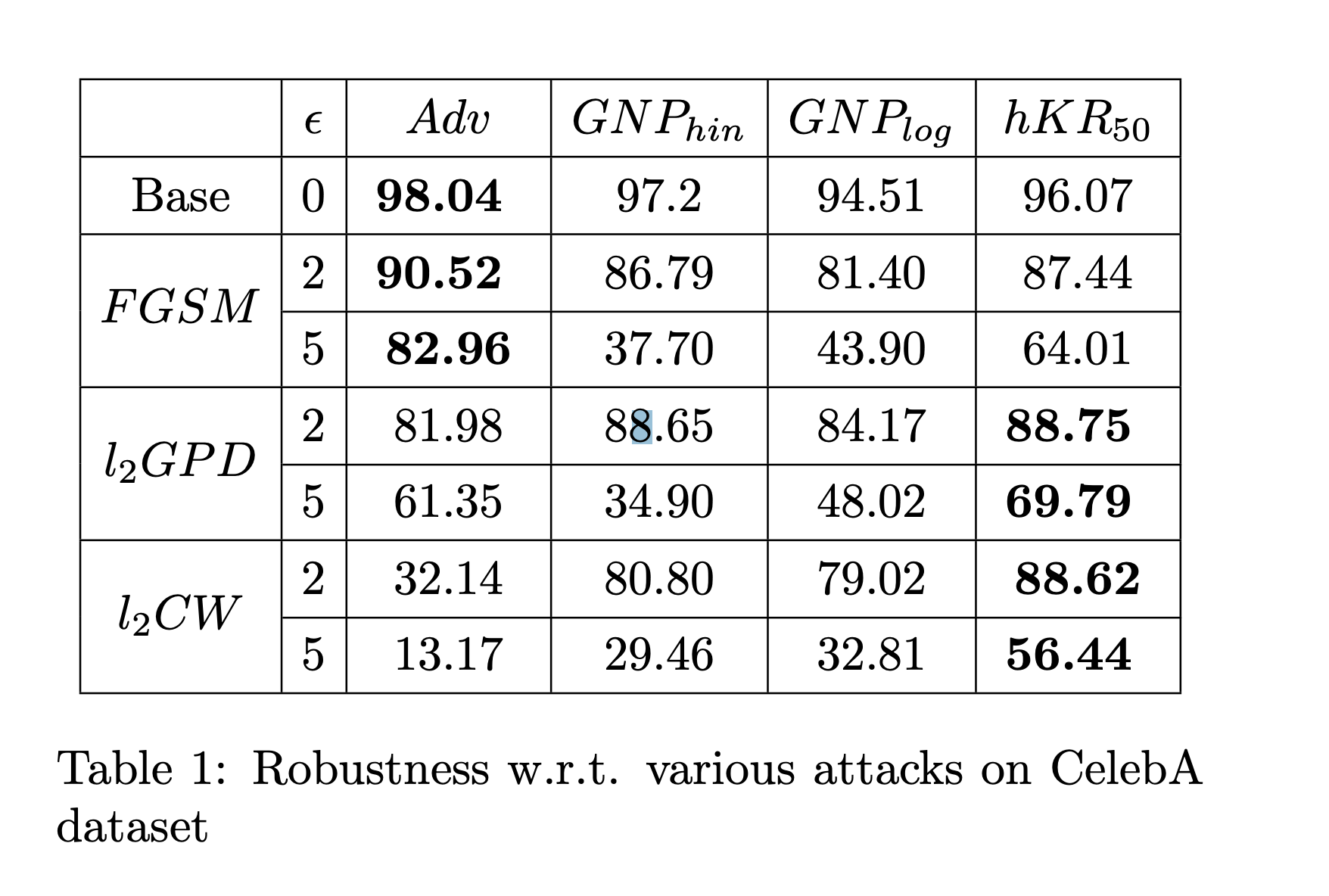
上記のTable1は、3つの攻撃手法に対する攻撃前(Base)と攻撃後の正解率をまとめています。なお、4行目の$l_2GPD$は$l_2PGD$の表記ミスです。
Table1を確認すると、攻撃前の正解率では$Adv[$6]で提案されている手法が最も良いですが、リプシッツ制約を受けている$GNP$系の手法と比較すると提案手法である$hKR$が良いことがわかります。
3つの攻撃手法を受けた後の正解率を確認すると、$FGSM$に対してのみ$Adv$[6]で学習されたモデルの正解率が高いですが、それ以外では**$hKR$で学習されたモデルの正解率が良い**ことがわかります。
これによりhKRが有効であることが実験的に示されました。
以下に、今回比較した5つの防御手法で学習されたモデルに対して行われたadversarial attackで出力されたadversarial exampleの例を示します。
ノイズで顔が覆われているがいらっしゃることがわかります。防御手法ごとにノイズの加わり方が異なるのは面白いですね。
次に読むべき論文は?
今回は、CVPR2021で発表された防御手法について解説しました。CV関連でadversarial attackの話題は毎年議論されるので、非常に多くの論文があります。
例えば、同じCVPR2021に掲載されている
Enhancing the Transferability of Adversarial Attacks through Variance Tuning
は、タイトルから推察する限り、adversarial exampleの転移性に着目して、転移性を高めるための攻撃手法を開発していると思います。この転移性を利用してblack box attackができたりするので転移性を高める研究は非常に重要だと考えています。
全てのCVPR2021の論文には目を通せていないので、追加がありましたら次の記事で記載します。
Reference
[1]: Earth Mover's Distance (EMD)
[2]: Improved Training of Wasserstein GANs
[5]: SPECTRAL NORMALIZATION FOR GENERATIVE ADVERSARIAL NETWORKS
[6]: Towards Deep Learning Models Resistant to Adversarial Attacks
[7]: Parseval Networks: Improving Robustness to Adversarial Examples
[8]: Preventing Gradient Attenuation in Lipschitz Constrained Convolutional Networks
[9]: DeepFool: a simple and accurate method to fool deep neural networks
Appendix: リプシッツ性、リプシッツ連続
2つの距離空間$(x,d_x)$, $(Y, d_Y)$に対して、写像$f:X\rightarrow Y$がリプシッツ連続であるとは、定数$K\geq 0$が存在して
$$d_Y(f(x_1), f(x_2))\leq Kd_X(x_1, x_2) ~ (\forall x_1, x_2 \in X))$$
を満たすことである。定数$K$自身、またその最小のものをリプシッツ定数と呼ぶ。特に$K<1$のとき、縮小写像とよばれる。
- 一階微分が有界な任意の関数はリプシッツである。
- 微分方程式における解の一意性はこの性質から導かれる。