はじめに
本記事は、LabVIEWを使った主成分分析について解説しています。
パルマーペンギンデータに対して、主成分分析をおこない、約90%の情報量を保持したまま2次元データへ次元圧縮可能なことを確認できました。
LabVIEWによる統計処理作成の際に参考になれば幸いです。
パルマーペンギンデータセット
有名なアイリスデータセットに取って代わることを目標としたデータセットのようです。パルマー諸島に生息するアデリーペンギン、ジェンツーペンギン、ヒゲペンギンの3種のペンギンについて、生息する島、くちばしの長さ、くちばしの高さ、羽の長さ、体重、性別、西暦のデータが格納されています。アデリーペンギンはスイカペンギンのモデルのようです。
palmerpenguins
https://allisonhorst.github.io/palmerpenguins/
くちばしの長さ、高さ、ひれの長さ、体重をペアプロットした結果

処理の流れ
データセットから抽出した、オスのくちばしの長さ、くちばしの高さ、ひれの長さ、体重のデータに対して主成分分析をおこない、第1、第2主成で散布図を作成しました。
処理の流れは以下のとおりです。
- データセットをcsv形式で保存する。(*Pythonで実行)
- LabVIEWでcsvファイルを読み込む。
- 標準化する。
- 共分散行列を求める。
- 共分散行列の固有値と固有ベクトルを求める。
- 第1,第2,第3,第4主成分がなす空間へ標準データを射影する。
- 第1,第2主成分を抽出し散布図を作成する。
処理の説明
順番に処理を説明します。
1.データセットをcsv形式で保存する。(*Pythonで実行)
オスのデータを抽出した後、データをcsvファイルへ書き出します。
from palmerpenguins import load_penguins
penguins = load_penguins()
male = penguins.query("sex == 'male'")
male.to_csv("./penguins_male.csv",
columns=["bill_length_mm", "bill_depth_mm","flipper_length_mm", "body_mass_g","species"],index=False)
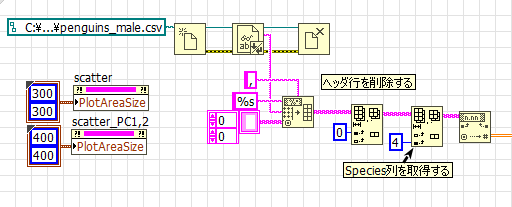
2.LabVIEWでcsvファイルを読み込む。
左下の処理で散布図が正方形となるようサイズを調整しています。
3.標準化する。
読み込んだデータを、平均値=0、分散=1に標準化します。

下図は元のデータと標準化したデータを散布図にプロットした結果です。
くちばしの長さ、くちばしの高さ、ひれの長さ、体重、すべてのデータを標準化していますが、ここでは2次元で表現するため、くちばしの長さと高さのデータを抽出し散布図を作成しています。
赤の標準化データの中心が0付近へ移動していることが確認できます。

4.共分散行列を求める。
元データと標準化後のデータに対して、Covariance Matrix.viを使い共分散行列を求めました。

標準化データの対角成分が1付近となっていることが確認できます。
Covariance Matrix.viは不偏分散を返します。

5.共分散行列の固有値と固有ベクトルを求める。
Eigenvalues and Vectors.viを使い算出しました。
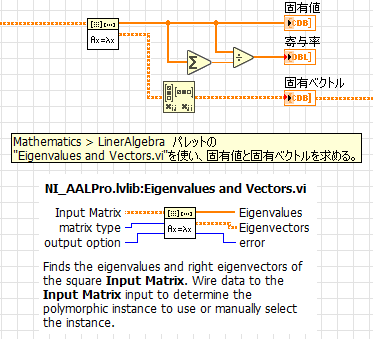
下図が結果です。
固有ベクトルは、元データの分散が大きい方向をあらわすベクトルです。第1主成分がもっとも分散が大きい方向となります。
固有値は、各主成分方向における分散をあらわします。
寄与率は、各主成分がもつ分散の比率になり、ペンギンデータの場合、第1、第2主成分でおおよそ90%の情報を持っていることになります。
つまり、4次元のデータから第1,第2主成分の2次元のデータへ圧縮した場合においても、全体の90%の情報を保持していることになります。

6.主成分がなす空間へ標準データを射影する。
固有ベクトルを列の要素とする行列と標準化データを掛け算し、第1,第2,第3,第4主成分がなす空間へ標準データを射影します。
ここでもLabVIEWの標準関数を使って行列積を計算しています。

7.第1,第2主成分を抽出し散布図を作成する。
第1,第2主成分を抽出しXYグラフを使って散布図を作成しました。


まとめ
LabVIEWでも問題なく主成分分析処理の実装が実現できました。
LabVIEWはマウス操作でGUIを自由自在に編集できるので、結果のビジュアライズを楽に実現できました。


