CourseraのMachine Learningを受講したのは1年ぐらい前であるが,機械学習の基本をしっかり学ぶことができたと実感している.「交差エントロピー」は分類問題で用いられる誤差関数であるが,今一度,概念を頭にたたき込むことを目的として,Coursera MLのweek2,ロジスティック回帰の課題を行った.実際,コースではMatlab(またはOctave)が用いられていたが,ここではPythonを用いる.
(プログラミング環境:Python 2.7.11, numpy 1.11.0, scipy 0.17.0, tensorflow 0.9.0rc になります.)
交差エントロピーとは
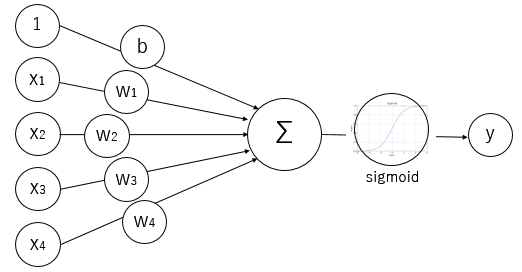
まず,分類問題におけるロジスティック回帰のモデルをながめてみる.
Fig. ロジスティック回帰のモデル
入力値 x1, x2, ...xn に対し重みをつけて合算し,それを活性化関数であるsigmoid関数を通して推定値を得るモデルである.上図では重み w1, w2, ...wn とバイアス値b としているが,Courseraの説明ではwとbをまとめてパラメータ theta としている.
交差エントロピーは,「上記モデルの推定値が実際の値に対し,どれぐらい違っているか」を表す数値である.次の式で表される.(英語は cross entropy, xentropy, xent と略されることもあります.)
J(\theta) = \frac{1}{m}\sum_{i-1}^{m} [-y^{(i)}\ log(h_{\theta} (x^{(i)})) - (1-y^{(i)})\ log(1-h_{\theta}(x^{(i)}))]
\\
(h_{\theta}(x) = g(\theta^{T}x),\ g(z) = \frac{1}{1+e^{-z}})
ここで,h_theta(x) は,推定値.二値分類問題における推定値であるので,分類 y=1 である確率 [0.0 ... 1.0] である.また,y^(i) が,訓練データとして与えられる実際のクラス (0 or 1) である.この誤差関数(Courseraではコスト関数)J (theta) を最小化するパラメータ値 thetaを求めることで精度の高いモデルを得るというのが,ロジスティック回帰の流れである.関数最小化の最適化プロセスにおいて誤差関数の導関数(gradient)が必要になるが,これは次の通りである.
\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}
これらの式を元に,Pythonのコードを作成していく.
Scipy.Optimize を用いた実装
コースでの課題の進め方にならい,まずコスト関数を求めるコードを作る.
import numpy as np
def sigmoid(x):
s = 1. / (1. + np.exp(-x))
return s
def compute_cost(theta, xm, ym, lamb):
'''
function:
compute the cost of a particular choice of theta
args:
theta : parameter related to weight, bias
xm, ym : data of features, labels
'''
m, n = xm.shape
xent = 0.0
logits = np.dot(xm, theta)
for i in range(m):
# J calculation, J is scalar
sigmd_x = sigmoid(logits[i])
xent += 1. / m *(-ym[i] * np.log(sigmd_x) - (1. - ym[i])
* np.log(1.0 - sigmd_x))
xent = np.asscalar(xent)
# add regularization term to cost
theta_sq = sum([item **2 for item in theta[1:]])
cost = xent + lamb /2. /m * theta_sq
return cost
まず,sigmoid関数を定義する.次に,compute_cost()で上記の交差エントロピー式に基づきコストを算定している.上のコードはデータサンプルごとにforループ内で変数 xent を足し合わせているが,効率化のためには,forループを使わない方がいいのだが,最初のコードとしてはこれでいいと思う.交差エントロピー xent を算定した後,Overfittingを防ぐための L2ノルム(重み減衰)項を付加してコスト cost としている.
Deep Learning frameworkでは,パラメータの偏微分(gradient)は自動的に計算してくれるが,Scipy + Numpy で実装する場合は自前で偏微分を求める必要がある.
def compute_grad(theta, xm, ym, lamb):
'''
function:
compute the cost gradient of a particular choice of theta
args:
theta : parameter related to weight, bias
xm, ym : data of features, labels
'''
m, n = xm.shape
xent_grad = np.zeros_like(theta)
logits = np.dot(xm, theta)
for i in range(m):
# grad(J) calculation
sigmd_x = sigmoid(logits[i])
delta = sigmd_x - ym[i]
xent_grad += 1. / m * (delta * xm[i])
xent_grad = xent_grad.flatten()
theta = theta.flatten()
# add regularization term to grad
cost_grad = np.zeros_like(xent_grad)
cost_grad[0] = xent_grad[0]
cost_grad[1:] = xent_grad[1:] + lamb / m * theta[1:]
return cost_grad
基本的に式をそのままコードに直しているが,後半で正則化項を付け加えている.(Coursera課題の進め方に従ってプログラムを作成しています... )
Couseraの課題では,最適化プロセス用の関数が用意されていてそれを用いて課題を解く流れとなっているが,今回は,Scipyの機能 scipy.optimize.minimize を用いる.
from scipy import optimize
def compute_cost_sp(theta):
global xmat, ymat, lamb
j = compute_cost(theta, xmat, ymat, lamb)
return j
def compute_grad_sp(theta):
global xmat, ymat, lamb
j_grad = compute_grad(theta, xmat, ymat, lamb)
return j_grad
if __name__ == '__main__':
x_raw, ymat = load_data(DATA)
xmat = map_feature(x_raw[:,0], x_raw[:, 1])
m, n = xmat.shape
theta_ini = np.zeros((n, 1))
lamb = 1.e-6
print('initial cost ={:9.6f}'.format(
np.asscalar(compute_cost_sp(theta_ini))))
res1 = optimize.minimize(compute_cost_sp, theta_ini, method='BFGS',
jac=compute_grad_sp, options={'gtol': 1.e-8, 'disp': True})
print('lambda ={:9.6f}, cost ={:9.6f}'.format(lamb, res1.fun))
コスト関数算定,その導関数算定の関数をwrapする関数を用意し,それと各オプションと合わせて,Scipyのoptimize.minimize() に入力している.これを実行すると以下のように最適解が求まる.(wrapperを用意したのは,パラメータ theta を明示することにより可読性向上させる目的です.)
initial cost = 0.693147
Optimization terminated successfully.
Current function value: 0.259611
Iterations: 555
Function evaluations: 556
Gradient evaluations: 556
lambda = 0.000001, cost = 0.259611
データセットが小さいこともあるが,イテレーション回数 555 の状況でも非常に短時間で解を求めることができた.
話が前後するが,この課題では,2つの特徴量(x1, x2)を持つデータから,高次の特徴量を生成して(マップして)それを用いて計算を行っている.
mapFeature(x) = [1,\ x_1,\ x_2,\ x_1^2,\ x_1x_2,\ x_2^2,\ ...\ ,\ x_2^6] ^ T
Pythonコードは次の通り.
def map_feature(x1, x2):
degree = 6 # accordint to coursera exercise
m = len(x1)
out = np.ones((m, 28))
index = 1
for i in range(1, degree+1):
for j in range(i+1):
out[:, index] = x1[:] ** (i-j) * x2[:] ** j
index += 1
return out
上記の通り,6次までを考慮し,さらにx1とx2の交互作用項も入れて28の特徴量に展開してモデルを作成している.統計モデリングの教科書には出てくるが,このような処理をプログラミングする機会が少ないと気がした.その理由であるが,ニューラルネットワーク・モデルを用いる場合,(今回は一層のロジスティック回帰であるが,)2層以上の多層モデル(Multi-layer model)とすることが多く,そのモデル上で高次モデルを表現できるので,mapFeature() 処理が不要となっていると考えられる.今回のmapFeature()では6次の次数までを考慮しているが,これに代わり6層のMulti-layer Perceptron (MLP) モデルで同様の分類機能を持った計算ができると予想される.
TensorFlowを用いた実装
次にTensorFlowを用いた実装を行ってみた.Scipy.Optimizeのコードを先につくったのでそれほど労力はかからない.
def compute_cost_tf(theta, x, y_, lamb):
logits = tf.matmul(x, theta)
pred = tf.sigmoid(logits)
xent = -1. * y_ * tf.log(pred) - (1. - y_) * tf.log(1. - pred)
# xent = tf.nn.sigmoid_cross_entropy_with_logits(logits, y_)
xent_mean = tf.reduce_mean(xent)
L2_sqr = tf.nn.l2_loss(w)
cost = xent_mean + lamb * L2_sqr
return cost, pred
TensorFlow には,sigmond関数 tf.sigmod() もあるし正則化の重み減衰項を求める tf.nn.l2_loss() もサポートされている.さらにありがたいことに,xent = -1. * y_ * tf.log(pred) - (1. - y_) * tf.log(1. - pred) の計算に対して関数 tf.nn.sigmoid_cross_entropy_with_logits() を用いることもできる.
(このtf.nn.sigmoid_... 関数のドキュメント にはロジスティック回帰のコスト関数について詳しい説明が載っているので参考になります.)
この後,TensorFlowのご作法にのっとってプログラムを作成した.
if __name__ == '__main__':
x_raw, ymat = load_data(DATA)
xmat = map_feature(x_raw[:,0], x_raw[:, 1])
# Variables
x = tf.placeholder(tf.float32, [None, 28])
y_ = tf.placeholder(tf.float32, [None, 1])
w = tf.Variable(tf.zeros([28, 1], tf.float32))
lamb = 1.0 / len(xmat)
cost, y_pred = compute_cost_tf(w, x, y_, lamb)
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
delta = tf.abs((y_ - y_pred))
correct_prediction = tf.cast(tf.less(delta, 0.5), tf.int32)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# Train
init = tf.initialize_all_variables()
with tf.Session() as sess:
sess.run(init)
print('Training...')
for i in range(10001):
batch_xs, batch_ys = xmat, ymat
fd_train = {x: batch_xs, y_: batch_ys.reshape((-1, 1))}
train_step.run(fd_train)
if i % 1000 == 0:
cost_step = cost.eval(fd_train)
train_accuracy = accuracy.eval(fd_train)
print(' step, loss, accurary = %6d: %8.3f,%8.3f' % (i,
cost_step, train_accuracy))
# final model's parameter
w_np = sess.run(w)
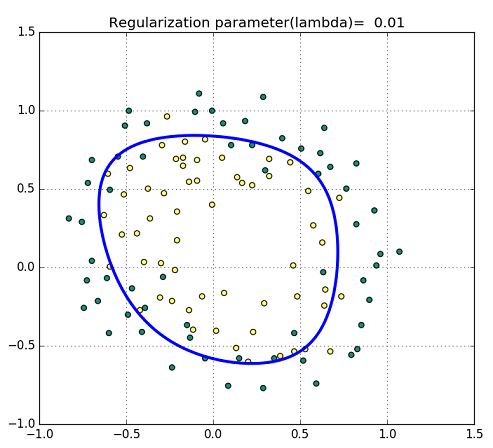
正則化の係数(lambda)により状況は異なるが,分類を行った結果の図は次のようになった.
Fig. Training data with decision Boundary
今回,Cousera Machine Learningのweek2の教材に従い,交差エントロピーの概念について振り返ってみた.改めて教材の良さを実感できたが,興味はあるが未受講の方に対しては,時間を見つけて受講されることをお勧めしたい.
参考文献 / web site
- Cousera Machine Learning (by prof. Ng) Week 2 の課題テキスト (PDFテキスト)
- 深層学習(岡谷 氏 著)
- Scipyドキュメント Optimization and root finding (scipy.optimize)
http://docs.scipy.org/doc/scipy/reference/optimize.html - TensorFlowドキュメント https://www.tensorflow.org/
- Coursera Machine Learningの課題をPythonで: ex2(ロジスティック回帰)- Qiita
http://qiita.com/nokomitch/items/40fb63c40baa0239fb83 - Coursera / Machine Learningの教材を2度楽しむ - Qiita
http://qiita.com/TomokIshii/items/b22a3681cb17836c8f6e