はじめに
気象予報士の方々は,天気図の情報やエルニーニョ現象に絡む海水温度mapなどからシーズンの気温予想をたてている.今回,このような専門家知識によるものでなく,過去の気温情報データから「暑い夏」になるかの予想方法を調べてみた.
まずベースとなる気温のデータセットであるが,気象庁に「地球温暖化」に関する情報として「世界と日本の気温・降水量の長期変化傾向」に関するデータがあったのでそれを参照した.日本の年平均気温の他に,季節平均気温のデータがあったのでそちらを使うことにした.
整形した後のcsvファイルは,以下のような内容である.季節平均気温は,春(3~5月),夏(6~8月),秋(9~11月),冬(12~2月)のデータから成る.
# Data source : www.data.go.jp,,,,,,
# column1 - 日本の年平均気温偏差(℃),,,,,,
# column2 - 日本の年平均降水量偏差(mm),,,,,,
# column3..6 - 日本の季節平均気温偏差(℃) Mar-May, Jun-Aug, Sep-Nov, Dec-Feb,,,,,,
Year,temp_yr,rain_yr,spring,summer,autumn,winter
1898,-0.75,15.1,-0.98,-1.7,-0.53,-0.67
1899,-0.81,199.2,-0.27,-0.21,-0.6,-2.12
1900,-1.06,-43.3,-1.35,-1.09,-1.11,-0.41
1901,-1.03,48.6,-0.74,-0.89,-1.26,-0.87
1902,-1.03,154.7,-1.65,-0.87,-2.2,-0.43
1903,-0.77,266.2,0.73,-0.19,-1.5,-0.93
1904,-0.86,-48.6,-1.37,-0.75,-0.16,-1.68
1905,-0.95,256.9,-0.55,-1.45,-1.39,-0.86
(後略)
なんと1898年から100年以上にわたってデータが蓄積され公開されていた.また気温(降水量)データに関しては,気温のRaw Dataではなく,「累積的な平均値からの偏差」の値が公開されていた.
http://www.data.jma.go.jp/cpdinfo/temp/index.html
まず各季節の気温(偏差)を時系列にplotした.
** Fig. Seasonal Temperature Trend **
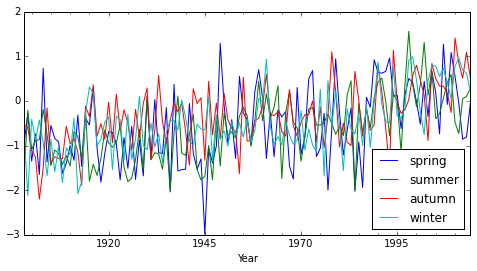
年ごと,シーズンごとに細かく変動しているようだ.分かりやすくするために10年分を平均する移動平均を pandas.rolling_mean() で算出し,plotした.(春,夏のみをplot.)
** Fig. Seasonal Temperature Trend (moving average) **
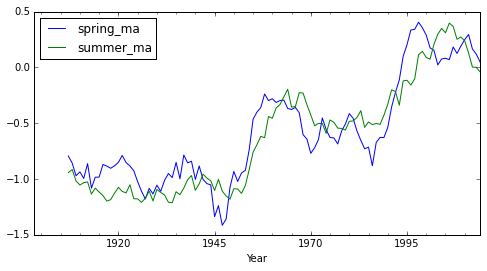
温暖化の状況が,右肩上がりの線で把握できる.また2本の線が似た動きをとっているので,「暑い夏を予想する」ことに少し期待が持てる感じである.
Linear Regression Model (OLS, 1 variable)
まず初めに,以下のようなモデルを考えた.
(その夏の気温偏差) ~ (直前の春の気温偏差)
statsmodels OLS() を用いて回帰分析を行った.
# Regression Analysis (OLS)
import statsmodels.api as sm
x1 = tempdf['spring'].values
x1a = sm.add_constant(x1)
y1 = tempdf['summer'].values
model1 = sm.OLS(y1, x1a)
res1 = model1.fit()
print res1.summary()
plt.figure(figsize=(5,4))
plt.scatter(tempdf['spring'], tempdf['summer'], c='b', alpha=0.6)
plt.plot(x1, res1.fittedvalues, 'r-', label='OLS(model1)')
plt.grid(True)
** Fig. 春の気温偏差(x-axis) vs. 夏の気温偏差(y-axis) **
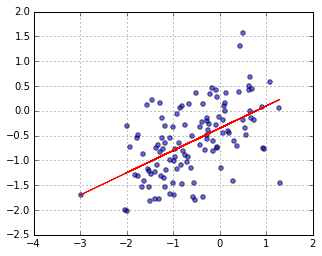
予想より相関度合いの低い結果である.Fitした線は,一応,正の相関を示している.summary() 情報は以下の通りであった.
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.282
Model: OLS Adj. R-squared: 0.276
Method: Least Squares F-statistic: 45.26
Date: Mon, 10 Aug 2015 Prob (F-statistic): 7.07e-10
Time: 16:39:14 Log-Likelihood: -107.55
No. Observations: 117 AIC: 219.1
Df Residuals: 115 BIC: 224.6
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const -0.3512 0.068 -5.148 0.000 -0.486 -0.216
x1 0.4489 0.067 6.727 0.000 0.317 0.581
==============================================================================
Omnibus: 0.159 Durbin-Watson: 1.571
Prob(Omnibus): 0.924 Jarque-Bera (JB): 0.075
Skew: 0.062 Prob(JB): 0.963
Kurtosis: 2.990 Cond. No. 1.88
==============================================================================
上記の通り,R-squared = 0.282 で相関は弱い.
Linear Regression Model (OLS, 2 vars, multiple)
やはり,春だけでなく,その前の冬の気温を関係しているかも知れないと考え,次のようなモデルを考えた.
(その夏の気温) ~ (冬の気温(6か月前))& (春の気温)
重回帰分析(Multiple Regression)のモデルである.DataFrameの各行には,同じ年の気温偏差が入っているので,(冬の気温)については shift() の処理をして前年のものを参照するようにしている.
# Regression Analysis (OLS: summer ~ b0 + b1*winter.shift(1) + b2*spring)
tempdf['winter_last'] = tempdf['winter'].shift(1)
X2 = tempdf[['winter_last', 'spring']].iloc[1:,:].values
X2a = sm.add_constant(X2)
y2 = tempdf['summer'].iloc[1:,].values
model2 = sm.OLS(y2, X2a)
res2 = model2.fit()
print res2.summary()
x2_model2 = res2.params[1] * tempdf['winter_last'] + res2.params[2] *tempdf['spring']
plt.figure(figsize=(5,4))
plt.scatter(x2_model2[1:], y2, c='g', alpha=0.6)
plt.plot(x2_model2[1:], res2.fittedvalues, 'r-', label='OLS(model2)')
plt.grid(True)
** Fig. 冬,春の気温偏差(x-axis) vs. 夏の気温偏差(y-axis) **
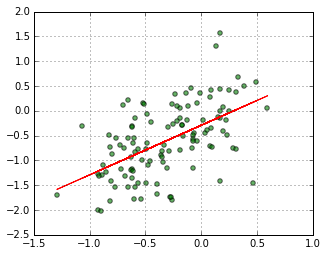
(OLS: summer ~ b0 + b1 x winter.shift(1) + b2 x spring)
R-squared = 0.303 で前のモデルからの変化はごくわずかである.回帰パラメータは次の通り.(summary() 出力からの抜粋.) x1 の P値(0.065)だけがやや大きい.
==============================================================================
coef std err t P>|t| [95.0% Conf. Int.]
------------------------------------------------------------------------------
const -0.2927 0.073 -4.007 0.000 -0.437 -0.148
x1 0.1609 0.086 1.863 0.065 -0.010 0.332
x2 0.3984 0.070 5.674 0.000 0.259 0.537
==============================================================================
R-squaredの数値から,このやり方では高精度の気温傾向予想はだいぶ難しいということが分かった.
PyMC3 Trial (Linear Regression)
上記までで「夏の気温予想」についてのほぼ勝負は見えてきたが,「弱い相関」という結論だけではつまらないので,MCMCのPython実装であるPyMC3を用いて回帰パラメータのベイズ推定を試してみることにした.(少し前でしたが,PyMC3のインストール際にはだいぶ苦労しました.)
問題の設定は,次の通り.
- 線形回帰モデルのベイズ推定.ここでのモデルは,上記2番目のモデル.
(summer ~ beta0(intercept) + beta1 x winter + beta2 x spring) - 無情報事前分布の考え方を適用し,分散sigmaの初期値は適当な分布を与える.
PyMC3のTutorialページを参考に,以下のcodeを用意してsimulationを行った.
# using PyMC3
import pymc3 as pm
model3 = pm.Model()
myX1 = tempdf['winter_last'].iloc[1:,].values
myX2 = tempdf['spring'].iloc[1:,].values
myY = y2
# model definition (step.1)
with model3:
# Priors for unknown model parameters
intercept = pm.Normal('intercept', mu=0, sd=10)
beta = pm.Normal('beta', mu=0, sd=10, shape=2)
sigma = pm.HalfNormal('sigma', sd=1)
# Expected value of outcome
mu = intercept + beta[0]*myX1 + beta[1]*myX2
# Likelihood (sampling distribution) of observations
Y_obs = pm.Normal('Y_obs', mu=mu, sd=sigma, observed=myY)
# run simulation (step.2)
from scipy import optimize
with model3:
# obtain starting values via MAP
start = pm.find_MAP(fmin=optimize.fmin_powell)
# instantiate sampler
step = pm.NUTS(scaling=start)
# draw 500 posterior samples
trace = pm.sample(500, step, start=start)
pm.summary(trace)
pm.traceplot(trace)
PyMC3 だが,source等がgithubに公開されているが,残念ながら現時点(2015/8)でドキュメントが決定的に不足している.これに自分自身のベイズ統計理論に関する理解不足を合わると二重苦,三重苦の状況である.今回分かった点としては...
- PyMC3 は,その前のバージョン(PyMC 2.x.x)とは(互換性という点で)別物.したがって,PyMCのドキュメントはあまり参考にならない.
- 自分のやりたい内容の例題python codeを探す.githubに(あまり豊富とは言えないが)example フォルダがあって,代表的な問題についてのcodeが用意されている.
- Class, Functionの引数など細かいところを知りたい場合は,ソースを見るしかなさそう.(ファイルのヘッダに説明が載っているのと,pythonの特徴で構成が見やすいことが救いである.)
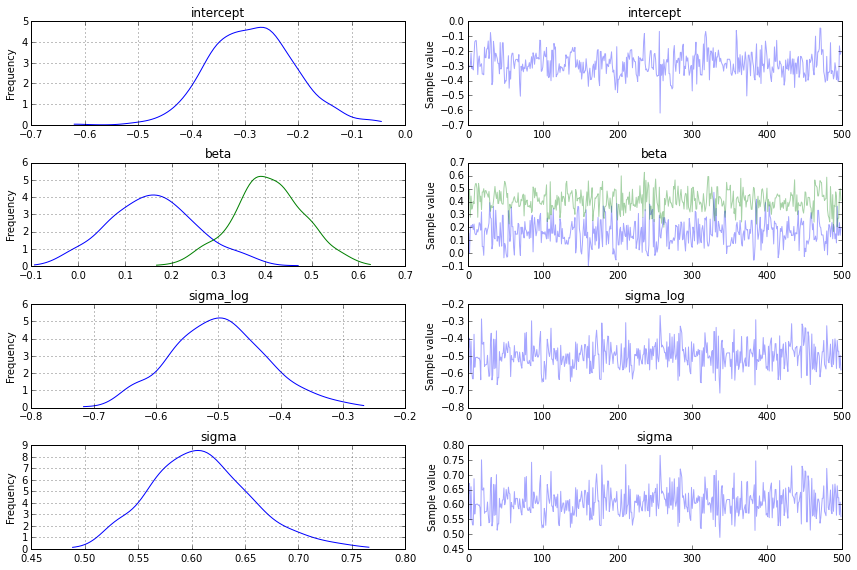
得られたsimulationの結果は,次の通り.
("sigma_log" の状況が出力される理由がよく分かりません...)
** summary(trace)の出力 **
intercept:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
-0.286 0.080 0.005 [-0.431, -0.127]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
-0.435 -0.341 -0.286 -0.235 -0.129
beta:
Mean SD MC Error 95% HPD interval
-------------------------------------------------------------------
0.161 0.095 0.005 [-0.024, 0.347]
0.407 0.077 0.004 [0.266, 0.568]
Posterior quantiles:
2.5 25 50 75 97.5
|--------------|==============|==============|--------------|
-0.017 0.095 0.159 0.222 0.361
0.252 0.362 0.405 0.459 0.559
(後略)
ここでは,OLSで出力されていた,95%信頼区間(C.I.)ではなく95% highest posterior density(HPD)が出力されている.(密度が高い事後分布区間,信用区間)個人的にはもう少し行間を詰めて(tightなフォーマットで)出力をお願いできたらと思う.
このsimulation結果から,scatter plotを作図した.
myX = trace['beta'][-1][0] *myX1 + trace['beta'][-1][1] *myX2
plt.figure(figsize=(5,4))
plt.scatter(myX, myY, c='g', alpha=0.6)
plt.grid(True)
for i in range(len(trace)):
plt.plot(myX, trace['beta'][i][0] *myX1 + trace['beta'][i][1] * myX2, color='blue', alpha=0.005)
** Fig. 冬,春の気温偏差(x-axis) vs. 夏の気温偏差(y-axis) **
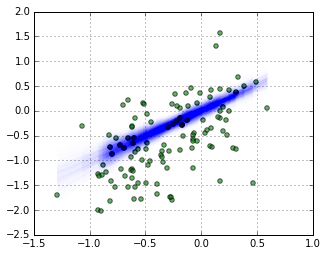
OLSとMCMC(PyMC3)の結果比較
| intercept | beta1 | beta2 | |
|---|---|---|---|
| OLS | -0.293 | 0.161 | 0.398 |
| MCMC(500step) | -0.286 | 0.161 | 0.407 |
| MCMC(10000step) | -0.291 | 0.163 | 0.397 |
回帰パラメータとしては,ほぼ等しい数値となった.
まとめと今後の課題
当初の目的「暑い夏を予想する」に対しては,やや期待外れの状況となってしまった.今回のモデルが単純過ぎたことが原因と思われるが,これは時系列分析の要素を取り入れたモデル(AR model等) 導入で改善できる可能性ありと考えている.
PyMC3についてはまだ使い始めたばかりで,ベイズ統計の理論も,モジュールの使いこなしについても,まだまだ勉強しなければならない.計算パラメータの調整や,収束状況の判定などやるべきことはたくさんある.(いい意味で,いじりがいのあるツール(おもちゃ)である.)
またPyMC3の情報不足は,関係者のドキュメント整備を待っている状況だが,すでに実績のあるBUGS,Stan等の例題を調べながらモデリングや分析手法への理解を深めていきたい.
参考文献 (web site)
- PyMC3 tutorial
https://pymc-devs.github.io/pymc3/getting_started/ - PyMC (previous version) documentation
http://pymc-devs.github.io/pymc/index.html - StatsModels documentation
http://statsmodels.sourceforge.net/stable/ - 気象庁(地球温暖化)
http://www.data.jma.go.jp/cpdinfo/index_temp.html - データ解析のための統計モデリング入門 (岩波書店)
https://www.iwanami.co.jp/cgi-bin/isearch?isbn=ISBN978-4-00-006973-1