試しに株価データにGLM（一般化線形モデル）を使ってみた

はじめに

２つの株価データの関係性を見る際，一般に両者の対数利益率が正規分布をとるという前提で分析に取り掛かる．しかしながら，実際の株価をみるとなかなかきれいな正規分布を見ることはないので，線形モデルを用いて回帰分析する際にも，出力される統計値に注意深く気を配る必要がある．

正規分布とならない関係性を扱うモデルとしてGLM(=Generalized Linear model, 一般化線形モデル)があるが，これを適用するためには統計モデリングの考え方を習得する必要があり，若干の技術的gapを感じているところである．しかしながら，python statsmodelsでサポートされていることもあり，今回，厳密なことをあまり考えずに「お試し」で使ってみることにした．

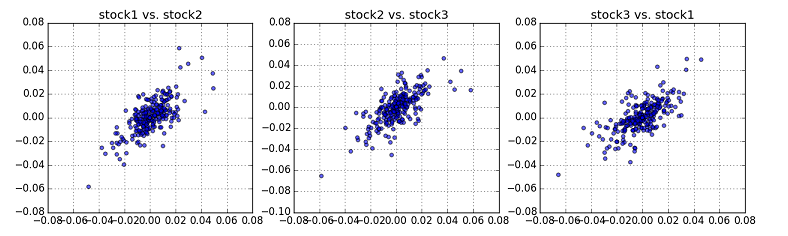
まず分析の対象として，東証１部の自動車関連銘柄（３社）をpick upした．３社から２社を選んだ3通りの組み合わせの対数利益率のScatter Plotは下図のようになる．

３つともあまり強くない（弱い）正の相関があることが確認できる．これら３つのうちから真ん中のデータ(stock2 vs. stock3）をとりあげ，回帰分析を行うことにした．因みにstock2は株価コード7203，stock3は株価コード7267の銘柄である．

線形モデル(Linear Model)の適用

まず初めに，Linear Modelを用いて回帰分析を行った．データ読み込み，および線形モデルの回帰分析までは以下のようなcodeとした．

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import statsmodels.api as sm

    
def my_tof(s):
	f1 = float(s.replace(',', ''))
	return f1

# pandas read_csv()
my_colmn = ['Date', 'Open', 'High', 'Low', 'Close', 'Diff', 'Volume', 'cH', 'cI', 'cJ', 'cK', 'cL', 'cM', 'cN', 'cO']

index = pd.date_range(start='2014/1/1', end='2014/12/31', freq='B')
stock_raw = pd.DataFrame(index=index)
mydf = pd.DataFrame(index=index)

stock1 = pd.read_csv('./x7201-2014.csv', index_col=0, parse_dates=True, skiprows=1, names=my_colmn, header=None)
stock_raw['stock1'] = stock1[::-1].loc[:, 'Close']
stock2 = pd.read_csv('./x7203-2014.csv', index_col=0, parse_dates=True, skiprows=1, names=my_colmn, header=None)
stock_raw['stock2'] = stock2[::-1].loc[:, 'Close']
stock3 = pd.read_csv('./x7267-2014.csv', index_col=0, parse_dates=True, skiprows=1, names=my_colmn, header=None)
stock_raw['stock3'] = stock3[::-1].loc[:, 'Close']

stock_raw.dropna(inplace=True)
stock_base_label = ['stock1', 'stock2', 'stock3']

for st in stock_base_label:
	st_price = st + '_p'
	st_return = st + '_ret'
	st_log_return = st + '_lgret'
	
	mydf[st_price] = stock_raw[st].apply(my_tof)
	mydf[st_price].fillna(method='ffill', inplace=True)
	mydf[st_return] = mydf[st_price] / mydf[st_price].shift(1)
	mydf[st_log_return] = np.log(mydf[st_return])

# scatter plotting
（中略）

# apply OLS model 
mydf.dropna(inplace=True)

x1 = mydf['stock2_lgret'].values    # stock2 log-return
x1a = sm.add_constant(x1)
y1 = mydf['stock3_lgret'].values    # stock3 log-return

# OLS (linear model)
md0 = sm.OLS(y1, x1a)
res0 = md0.fit()
print res0.summary()

plt.figure(figsize=(5,4))
plt.scatter(mydf['stock2_lgret'], mydf['stock3_lgret'], c='b', alpha=0.6)
plt.plot(x1, res0.fittedvalues, 'r-', label='Linear Model')
plt.grid(True)

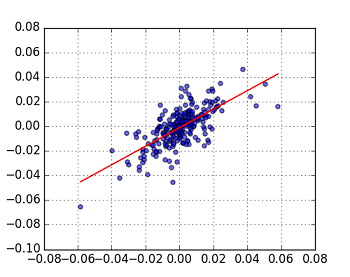
上の通り，statsmodels.api.OLS() を用いている．この結果，以下のグラフが得られた．

Fig. stock2 vs. stock3 (Log Return) Linear Model

GLM (Gaussian distribution)

次にGLMによる回帰分析を行う．statsmodelsのGLM（一般化線形モデル）では，使用できる確率分布(Familyと呼ばれる）として以下がサポートされている．（Documentより抜粋）

Families for GLM(Generalized Linear Model)

Family	The parent class for one-parameter exponential families.	Remark
Binomial	Binomial exponential family distribution.	二項分布
Gamma	Gamma exponential family distribution.	ガンマ分布
Gaussian	Gaussian exponential family distribution.	ガウス分布
InverseGaussian	InverseGaussian exponential family.	逆ガウス分布
NegativeBinomial	Negative Binomial exponential family.	負の二項分布
Poisson	Poisson exponential family.	ポアソン分布

また，各Familyに対して，使用できる（Combinationとなる）リンク関数が決まっている．(Documentより抜粋）リンク関数はオプション指定できるが，指定がない場合は，ディフォルトのものが使用されるようである．

	ident	log	logit	probit	cloglog	pow	opow	nbinom	loglog	logc
Gaussian	x	x				x
inv Gaussian	x	x				x
binomial	x	x	x	x	x	x	x		x	x
Poission	x	x				x
neg binomial	x	x				x		x
gamma	x	x				x

まず，Gaussian関数を用いて計算を行った．Codeは，以下の通り．

# apply GLM(Gaussian) model
md1 = sm.GLM(y1, x1a, family=sm.families.Gaussian())    # Gaussian()
res1 = md1.fit()
print res1.summary()

plt.figure(figsize=(5,4))
plt.scatter(mydf['stock2_lgret'], mydf['stock3_lgret'], c='g', alpha=0.6)
plt.plot(x1, res1.fittedvalues, 'r-', label='GLM(Gaussian)')
plt.grid(True)

Fig. stock2 vs. stock3 (GLM(gaussian dist.))

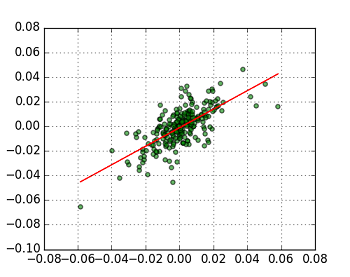
GLMがフィッティングした線は，上図から全く変化していないようである．計算結果のsummary()を比較する．

OLSのsummary

In [71]: print res0.summary()
                            OLS Regression Results
==============================================================================
Dep. Variable:                      y   R-squared:                       0.486
Model:                            OLS   Adj. R-squared:                  0.484
Method:                 Least Squares   F-statistic:                     241.1
Date:                Sun, 26 Jul 2015   Prob (F-statistic):           1.02e-38
Time:                        16:18:16   Log-Likelihood:                 803.92
No. Observations:                 257   AIC:                            -1604.
Df Residuals:                     255   BIC:                            -1597.
Df Model:                           1
Covariance Type:            nonrobust
==============================================================================
                 coef    std err          t      P>|t|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const         -0.0013      0.001     -1.930      0.055        -0.003  2.64e-05
x1             0.7523      0.048     15.526      0.000         0.657     0.848
==============================================================================
Omnibus:                       10.243   Durbin-Watson:                   1.997
Prob(Omnibus):                  0.006   Jarque-Bera (JB):               16.017
Skew:                          -0.235   Prob(JB):                     0.000333
Kurtosis:                       4.129   Cond. No.                         73.0
==============================================================================

GLM(Gaussian dist.)のsummary

In [72]: print res1.summary()

                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:                      y   No. Observations:                  257
Model:                            GLM   Df Residuals:                      255
Model Family:                Gaussian   Df Model:                            1
Link Function:               identity   Scale:                0.00011321157031
Method:                          IRLS   Log-Likelihood:                 803.92
Date:                Sun, 26 Jul 2015   Deviance:                     0.028869
Time:                        16:12:11   Pearson chi2:                   0.0289
No. Iterations:                     4
==============================================================================
                 coef    std err          z      P>|z|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const         -0.0013      0.001     -1.930      0.054        -0.003  2.02e-05
x1             0.7523      0.048     15.526      0.000         0.657     0.847
==============================================================================

２つの出力は内容がだいぶ異なっていることが分かる．

OLSでは，R-squared, AIC, BICの数値が出力されているが，GLMではこれらがなく，代わりにDeviance（逸脱度），Pearson chi2 統計量などが出力されている．両方にあるものとしては，Log-Likelihood（Log-尤度）の数値が出力されている．

GLMの出力からは，Link Functionが"identity"（恒等リンク関数）が設定されていることが分かる．また，OLSとGLMで偏回帰係数が同じ値(-0.0013, 0.7523)となっていることから，回帰分析の結果（内容）が同じであることが確認できた．

GLM (Gamma distribution)

次に分布としてガンマ分布(Gamma distribution)を使ったGLMの計算を試してみた．ガンマ分布が株価収益率をうまく表現するかどうかについては議論の余地があるかと思ったが，GLMらしい計算を試すことを目的にやってみた．

計算の実行で問題となったのが，対数株価収益率だと株価下落時にマイナスの値をとるがこれはガンマ分布の範囲外となってしまう．そこで対数を取る前の株価収益率をｙ値にして計算を行った．（少し無理やり感があることは否めないが...）

# apply GLM(gamma) model

x2 = x1 ; x2a = x1a
y2 = mydf['stock3_ret'].values    # replaced

md2 = sm.GLM(y2, x2a, family=sm.families.Gamma())
res2 = md2.fit()

# print summary and plot fitting curve
print res2.summary()
plt.figure(figsize=(5,4))
plt.scatter(mydf['stock2_lgret'], mydf['stock3_ret'], c='c', alpha=0.6)
plt.plot(x2, res2.fittedvalues, 'r-', label='GLM(Gamma)')
plt.grid(True)

y2_fit_log = np.log(res2.fittedvalues)
plt.figure(figsize=(5,4))
plt.scatter(mydf['stock2_lgret'], mydf['stock3_lgret'], c='c', alpha=0.6)
plt.plot(x2, y2_fit_log, 'r-', label='GLM(Gamma)')

Fig. stock2 vs. stock3 (GLM(gamma dist.))
(log - ident)

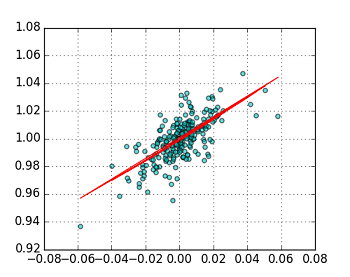
(log - log) （y値を変換した）

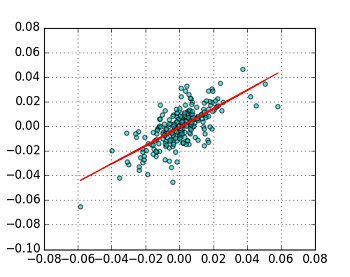
グラフとしては，同じような結果となった．summary()をながめてみる．

In [73]: print res2.summary()

                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:                      y   No. Observations:                  257
Model:                            GLM   Df Residuals:                      255
Model Family:                   Gamma   Df Model:                            1
Link Function:          inverse_power   Scale:               0.000113369003649
Method:                          IRLS   Log-Likelihood:                 803.72
Date:                Sun, 26 Jul 2015   Deviance:                     0.028956
Time:                        16:12:16   Pearson chi2:                   0.0289
No. Iterations:                     5
==============================================================================
                 coef    std err          z      P>|z|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const          1.0013      0.001   1502.765      0.000         1.000     1.003
x1            -0.7491      0.048    -15.470      0.000        -0.844    -0.654
==============================================================================

GLM(gaussian dist.)からGLM(gamma dist.)に変えて，微妙にLog-Likelihoodの数値やDevianceが変わっている．しかしモデルが改良できたというほどの変化がないことは確かである．y値を変換して計算したので，偏回帰係数は別物になってしまっている．

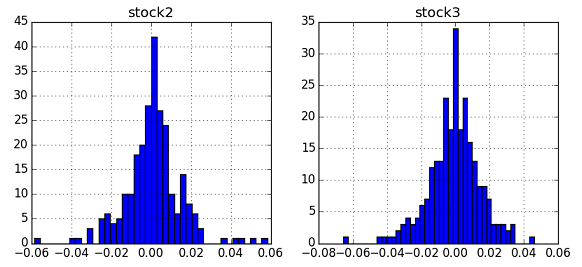
前後するが，データの正規性確認のため，stock2とstock3の対数収益率のヒストグラムを作図した．下図のような形状であった．

とりあえずの結論

今回のデータ分析においてGLM適用によるモデル精度向上は確認できなかった．これは同業種の株価（期間も1年程度）を見たため，複雑な（非線形な）関係となっていなかったためと考えられる．但し，今後いろいろなデータを分析するにあたり使えるツールが増えることは悪いことではないので，GLM他，高度な回帰分析手法について理解を深めていきたいと思う．

今回の（自動車メーカーA社株価 vs. B社株価）では威力を発揮しなかったが，少し毛色の違った組み合わせ，例えば（最高気温 vs. ビール会社株価）などで有効に使える可能性があると期待している．

参考文献

• statsmodelsドキュメント
  http://statsmodels.sourceforge.net/stable/glm.html

• 統計学入門（東京大学教養学部統計学教室 編）
  http://www.utp.or.jp/bd/978-4-13-042065-5.html

• データ解析のための統計モデリング入門（久保著，岩波書店）
  https://www.iwanami.co.jp/cgi-bin/isearch?isbn=ISBN978-4-00-006973-1