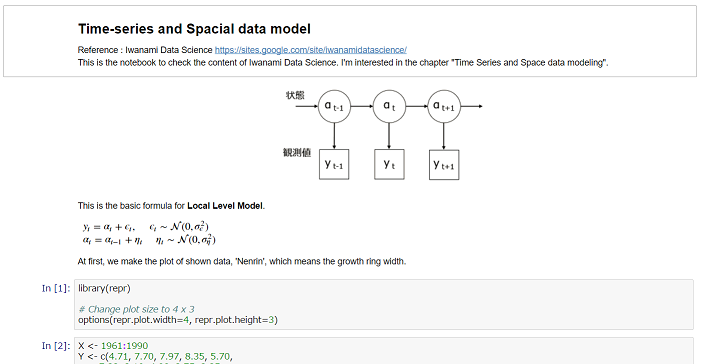
状態空間モデルの概略
ねた本は,岩波データサイエンス Vol. 1.([特集]ベイズ推論とMCMCのフリーソフト)
ここから状態空間モデルの概念図を引用する.
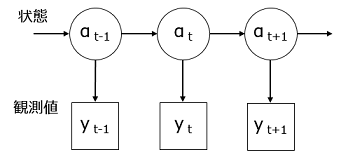
状態空間モデル(State-Space Model)とは,時系列の**「状態」があって,これをもとに一定のばらつきを含んだ「観測値」**が生成される,というものである.岩波データサイエンス Vol.1 は,「ベイズ推論とMCMCのフリーソフト」の特集だが,第3章全体が状態空間モデルに関する記事(伊東氏著)で,さらに他の章でも空間モデルの説明が出てくる.第3章では,RとJAGS(Just Another Gibbs Sampler)でこれを解く方法が説明されていた.
これを試すにあたり,当初,Python+PyMC3でやってみたがうまくいかなかった.
import pymc3
(略)
model1 = pm.Model()
with model1: # model definition
alpha0 = pm.Uniform('alpha0', lower=0. , upper=10.)
sigma_y = pm.Uniform('sigma_y', lower=0., upper=100.)
sigma_alp = pm.Uniform('sigma_alp', lower=0., upper=100.)
for i in range(1,N): # 以下2行がERROR. 状態量 α の定義したかった...
alpha[i] = pm.Normal(1, mu=alpha[i-1], sd=sigma[0])
y_obs = pm.Normal('y_obs', mu=alpha, sd=sigma[0], observed=ydat)
(略)
このようなコードを試したが,for ループのところ,状態量のモデル $\alpha_t = \alpha_{t-1} + \eta$ を定義する箇所でエラーとなる.考えてみれば,pymc3.Normal() (リストではpm.Normal() ) は,正規分布のモデルを生成するためのクラス・コンストラクタであるため,その引数の中に生成しようとするクラス(alpha[i-1])を含ませるのは難しいと考えられる.(いろいろInternetを調べましたが解決策は見つかりませんでした.)
このような状態空間モデル(または動的線形モデル)を扱える他のライブラリとして PyStan やカルマンフィルター系の実装 PyKalman等の使用を検討したが,今回はねた本にならって"R"を使うことにした.使用したプログラムは以下の通り.
- R ver.3.2.2
- Jupyter Notebook (notebookがver.4.0.6) + IRkernel ... 今回,初めてIRkernelを試してみました.
- JAGS ver.4.0.0 +{ rjags } パッケージ
- { dlm } パッケージ
Jupyter Notebook + IRkernel の環境について
Jupyter Notebook は,ご存知 IPython Notebook の更新版.言語処理系,カーネルを切り替えてPython以外も扱えるようになっている.(Jupyter = Julia + Python + R から名づけられたとのこと.)今回,R言語のためのIRkernelをインストールして使用した.
インストールの手順は次の通り.
- (必要があれば)R言語をインストール.
- R環境下で,IRkernel (https://github.com/IRkernel/IRkernel) をインストール.
install.packages(c('rzmq','repr','IRkernel','IRdisplay'),
repos = c('http://irkernel.github.io/', getOption('repos')))
IRkernel::installspec()
- コンソールにて ">Jupyte Notebook" で起動.(初め,いくつかRの依存パッケージ不足でerrorが発生しましたが,エラーメッセージの要求通りにRパッケージをインストールすることで起動できるようになりました.)
上の通り,ノートの新規作成メニューにて"R"を選択できる.
JAGSによる状態空間モデルの実装
ねた本「岩波データサイエンス Vol.1」の「時系列・空間データのモデリング」章に従い,以下のようなノートを作成していく.
これまでの IPython Notebookと同じく,Markdown文章と実行できるコードを混在することができる.また,Notebookの今回の更新から,MathJax の数式をオフラインでレンダリングできるのがうれしい.
Rで図形プロットする際のTipsを一つ.( NotebookのIn[1]: 記載のコマンドです.)
library(repr)
# Change plot size to 4 x 3
options(repr.plot.width=4, repr.plot.height=3)
このノートの後半で,{ggplot2} を使ってプロットを行っているが,何も指定しないと,Web Browserの幅いっぱいに合わせて図を生成する.(ほとんどの人は同じような状況になると思われるが)図がかなり大きく,文章,コードと合わせて表示されるとバランスがあまり良くない.{repr} は,IRkernerl と合わせてインストールされるサブ・パッケージであるが,この機能を使って上のようにオプション指定することにより,図を任意の大きさにできる.
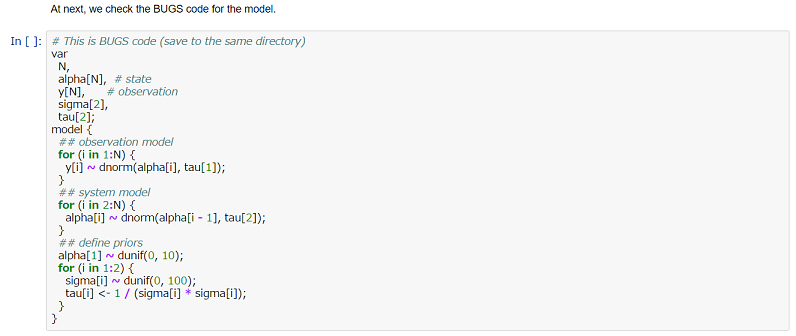
また,本ノートでは,直接実行するコードではないが,BUGSコードも一緒に記載している.
(JAGS + {rjags} では,BUGSコードを別ファイルに用意して,計算を実行する仕様である.)
全体をまとめるRコード,シミュレーションのモデルを定義するBUGSコード,計算結果出力と,ばらばらに散らばりがちな情報を一つにまとめることができるのは,Jupyter Notebookを使う大きな利点であると感じた.
このようにしてローカルレベルモデルで計算した,京都のスギの年輪幅の推移を以下のように図示した.
Fig. 'NenRin' growth width (by JAGS)
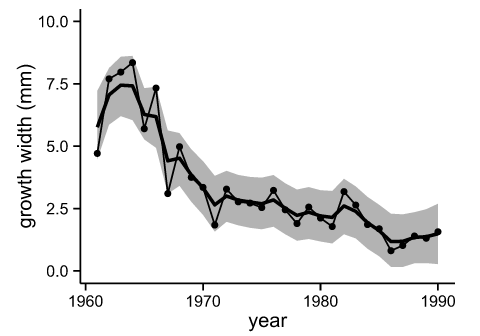
マーカーの付いた折れ線が観測値,太い実線がMCMCの計算により推定した値,灰色のエリアが95%の信用区間.
(Rのコードについては,「岩波データサイエンス」のサポートサイトから取得できます.)
{dlm} パッケージによる確認
JAGSはMCMC(Marcov chain Monte Carlo)の実装系である.MCMC以外に状態空間モデル(動的線形モデル)を扱える計算手法にカルマンフィルター系の実装があるが,"R"では,{dlm}, {KFAS} パッケージがよく使われるとのこと.今回は{dlm} パッケージを試してみた.
MCMCとカルマンフィルターの差異は「岩波データサイエンス」できちんと解説されている.(引用させていただきます... )「カルマンフィルタがMCMCと異なる点は,状態 $x_i$ については周辺事後分布を算出することができるが,$s^2$ , $\sigma^2$ のようなモデルのパラメータについては事後分布のひろがりを無視した推定(点推定)を行うことである.」 分散関係のパラメータのひろがり,言わば「ばらつきのばらつき」については(個人的には)あまり関心がなく,この点はまず問題とならない.
以下,作成したNotebookからRコードを引用する.
## Year and Growth width data(mm)
X <- 1961:1990
Y <- c(4.71, 7.70, 7.97, 8.35, 5.70,
7.33, 3.10, 4.98, 3.75, 3.35,
1.84, 3.28, 2.77, 2.72, 2.54,
3.23, 2.45, 1.90, 2.56, 2.12,
1.78, 3.18, 2.64, 1.86, 1.69,
0.81, 1.02, 1.40, 1.31, 1.57)
tsData <- ts(Y, frequency=1, start=c(1961, 1)) # Time Series data structure
n <- length(tsData)
library(dlm)
# Modeling function and initial parameters
mkModel1 <- function(parm){
dlmModPoly(order = 1, dV=parm[1], dW=parm[2])
}
myparm1 <- c(0.001, 0.001)
# Parameter calculation by fitting
dlmFit1 <- dlmMLE(tsData,
parm = myparm1,
build = mkModel1
)
# Filtering
oFitted1 <- mkModel1(dlmFit1$par)
oFiltered1 <- dlmFilter(tsData, oFitted1)
print(names(oFiltered1))
print(oFiltered1$f)
# Smoothing
oSmoothed1 <- dlmSmooth(oFiltered1)
print(names(oSmoothed1))
print(oSmoothed1$s)
以上でカルマンフィルターの計算結果が得られる.この結果を {ggplot2} でプロットする.
library(ggplot2)
base.family <- ""
ribbon.alpha <- 0.3
ribbon.fill <- "black"
alpha.mean <- dropFirst(oSmoothed1$s)
var_p <- unlist(dlmSvd2var(oSmoothed1$U.S, oSmoothed1$D.S))
alpha.up <- dropFirst(oSmoothed1$s) + qnorm(0.025, sd = sqrt(var_p[-1]))
alpha.low <- dropFirst(oSmoothed1$s) + qnorm(0.975, sd = sqrt(var_p[-1]))
p3 <- ggplot(data.frame(Year = X, Width = Y,
Width.mean = alpha.mean,
Width.up = alpha.up,
Width.low = alpha.low)) +
geom_ribbon(aes(x = Year, ymax = Width.up, ymin = Width.low),
fill = ribbon.fill, alpha = ribbon.alpha) +
geom_line(aes(x = Year, y = Width.mean), size = 1) +
geom_line(aes(x = Year, y = Width)) +
geom_point(aes(x = Year, y = Width), size = 2) +
xlab("year") +
ylab("growth width (mm)") +
ylim(0, 10) +
theme_classic(base_family = base.family)
print(p3)
Fig. 'NenRin' growth width (by {dlm})
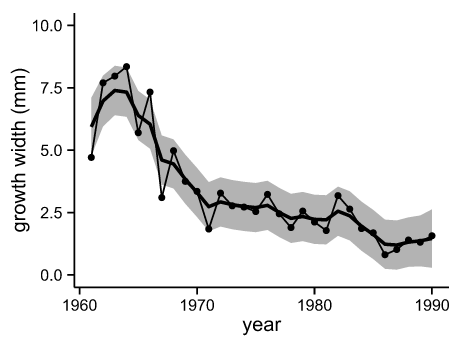
細かく見ると95%信頼区間を示す灰色エリアの大きさが若干異なるが,上に示したJAGSによる結果とほぼ一致した.
普段Pythonを使うことが多いのでPythonのカルマンフィルター系の実装も調べてみたいと考えている.今回 Jupyter Notebookを使ってみたが,"R"のデータ分析に見通しの良さを与えてくれることを実感した.因みに,Jupyter Notebookの事例として ”Kalman and Bayesian Filters in Python” がGithubに公開されているので,関心のある方にはお勧めである.
(結構な量の内容なので,少しずつ読み進めています.アニメーション等も使われていますし,Jupyter Notebookなので直接コードを動かすこともできます.リンクを以下に記載します.)
参考文献 (web site)
-
「岩波データサイエンス」サポートページ
https://sites.google.com/site/iwanamidatascience/ -
IRkernel - GitHub
https://github.com/IRkernel/IRkernel -
ローカルレベルモデル - Logic of Blue
http://logics-of-blue.com/%E3%83%AD%E3%83%BC%E3%82%AB%E3%83%AB%E3%83%AC%E3%83%99%E3%83%AB%E3%83%A2%E3%83%87%E3%83%AB/ -
状態空間時系列分析入門」をRで再現する http://elsur.jpn.org/ck/
-
{dlm} パッケージ添付のマニュアル (dlm: an R package for Bayesian analysis of Dynamic Linear Models)
-
"Kalman and Bayesian Filters in Python”
https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python