論文
この記事は下記の論文の内容をまとめたものである。
DellaPosta, D., Shi, Y., & Macy, M. (2015). Why do liberals drink lattes?. American Journal of Sociology, 120(5), 1473-1511.
概要
実際の調査データ(GSS)を使用して、個人のライフスタイルの相関は社会経済的な変数だけでは説明できないことを示したのち、エージェントベースモデルを用いて社会的影響と同類原理の双方を考慮した実験を行なった。これまでの調査ではランダムサンプリングが仮定されていたため、個人が持つ関係からのダイナミックな影響を考慮することはできなかった。しかし、エージェントベースモデルでそのような相互作用を考慮するモデルが可能となる。個人のライフスタイルの相関を説明するには、このようなモデルが必要であることを指摘した論文。
ライフスタイルと政治的イデオロギーの相関
ライフスタイル(趣味、好きな音楽のジャンル、結婚に対する考え等)は政治的イデオロギーと無関係のように思えるが、先行研究でも示唆されてきたように人々のライフスタイルと相関している。本研究ではまずそのことについて1972年から2010年のGSSデータ(アメリカ全土を対象とした大規模なアンケートデータ)を用いて示す。その前に、まずはライフスタイル同士の相関を確認する。
上記のデータから216のライフスタイルに関する質問項目を選定した。それらはGSSデータの年度にネストされた関係になっている(例えば、2008年、2009年、2010年にライフスタイルAとライフスタイルBの項目がある)。よって、線形混合モデルを使用しMCMCでパラメータを推定する(使用したのはRのMCMCglmmパッケージ)。
より正式に定式化すると下記の式を推定する。
$$
|r|_{j,t} = \alpha _{j} + \beta _{j} t + e _{j,t}
$$
${}$ここで$j$はライフスタイルに関する質問のあるペアを表し、$t$はGSSデータの年度を表す。$\beta_j$はある年度$t$固有の効果であり、$e_{j,t}$は誤差である。また、$\alpha_j$は年度に依存しない共通の相関関係の強さを表す。
上記に加えて共変量として10の社会経済的変数を考慮する。それらは、婚姻状況、親の存在、宗教、地域、最終学歴、世帯年収、居住地の大きさ、性別、出生コーホート、人種である。
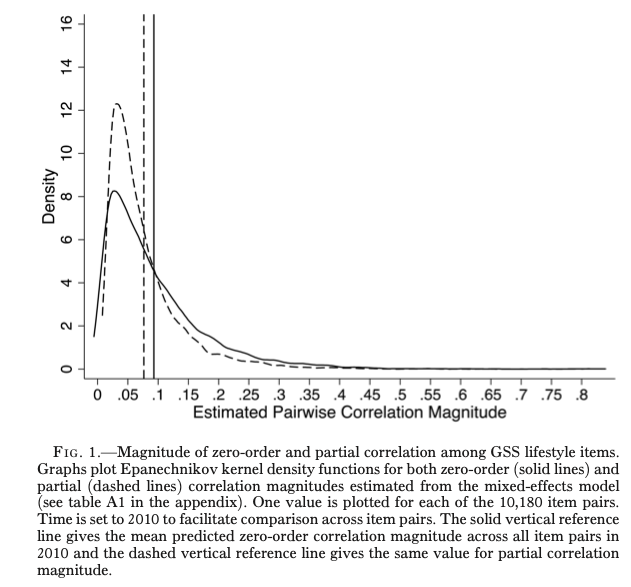
結果は下記の通りである。下記の図は$|r|_{j,t}$をヒストグラムにしそれをカーネル密度推定で平滑化したもである。実線が上記の社会経済的変数を考慮していない時、点線がそれを考慮した時である。なお、垂直線はその平均値である。
${}$ここからわかるように、社会経済的変数を考慮すると相関関係が弱くなるが、それはほんのわずかだけである。2010年のデータを詳細に確認すると、例えば「婚姻前の性行為は常に間違えである」に賛成した者はバーで夜を過ごす時間が短かったりする(社会経済的変数考慮前:$|r|=.30$ 社会経済的変数考慮後:$|r|=.19$)。このような相関は驚くことではないが、一方で「婚姻前の性行為は常に間違えである」に賛成した者は現代的なロックを好まない傾向にある(社会経済的変数考慮前:$|r|=.30$ 社会経済的変数考慮後:$|r|=.16$)といった一見関係のないライフスタイル同士が相関を示していた。
続いて上記と同様のやり方で政治的イデオロギーとライフスタイルの相関を分析した。その結果、2010年の場合その相関の(絶対値の)平均は社会経済的変数を考慮する前が.12、考慮後が.10となった。より詳細に確認すると一部のライフスタイルとの相関は社会経済的変数を考慮すると減少したが、増加したものもあった。また、216のライフスタイルに関する質問のうち54%が.10より大きな相関関係にあり、34%が.15より大きな相関にあった。そのうち89%が社会経済的変数を考慮しても.10より大きな相関関係にあった。
上記の結果は、ライフスタイル(趣味、好きな音楽のジャンル、結婚に対する考え等)は政治的イデオロギーと無関係のように思えるが、先行研究でも示唆されてきたように人々のライフスタイルと相関していることを改めて示唆する結果であり、なんらかの説明が必要である。特に、社会経済的変数を考慮しても相関関係に大きな減少が確認できないことを考えると、社会経済的変数だけでそれを説明するのは困難であると考えられる。
問題の背景
これまでの先行研究では伝統的に上記のライフスタイルの違いをジェンダーや学歴、社会階層といった違いによって説明しようとしてきた。しかし上記の結果からはライフスタイルの説明は社会経済的な変数だけでは説明できないことを示唆している。例えばリベラルは科学に対して好意的な態度をとる一方で、スピリチュアルなものに対しても好意的な態度をとっていた。このような事実を考えると、単にジェンダーや学歴、社会階層が人々のライフスタイルを形成していると考えるには無理がある。だからといって、個別具体的なライフスタイルそれぞれについて固有の理論で説明するのも困難である。
これまでのランダムサンプリングをベースとしたやり方では、個人が他の個人とは独立しているという仮定のもとで分析が実施されてきた。そこで本研究ではそのような方法を取らず人々の関係に着目した分析、説明(relational explaination)を行う。そこでは同類原理(ホモフィリー)と社会的影響(Social Influence)という2つの原理が想定される。社会的影響とは人々は他者からの影響を受けて自身の考えや態度をその他者に類似するように変更したり、あるいはその他者から離れるように変更したりすることである。同類原理とは類似した人は集まりやすいといった傾向を指す。このような原理に基づいて、なぜ政治的イデオロギーとライフスタイルの相関が存在するのかについて分析、説明を行う。
${}$GSSも含めてこれまでのデータはランダムサンプリングをベースとしており、人々の関係を考慮することはできない。そこで本研究ではエージェントベースモデルを使用する。
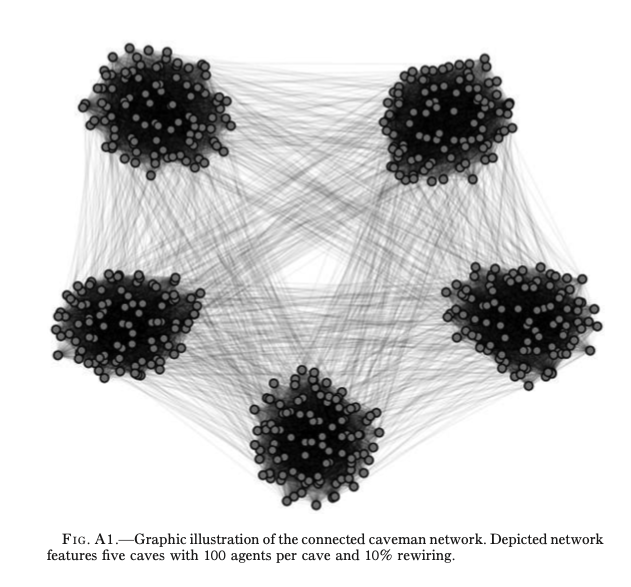
${}$そこではまず、$n$人のエージェントが自身と同一のcave内で$k$人とのエージェントとリンクしているconnected caveman graphを考える。なお、caveの数は$\frac{n}{k+1}$である。本研究では$k=99$としている(すなわち同一のcaveに100人のエージェントが存在している)。その上で、ある割合$\phi$のエッジをランダムに選択し次数を固定した上でエッジを書き換える。例えば、ノードA、B、C、Dが存在したとする。AとBにエッジが存在し、CとDにエッジが存在したとする。仮にAとBのエッジが選択され、AとBのエッジがAとDのエッジに書き変わったとする。そうするとDの次数は1から2になるため、DはCとのエッジをBとのエッジに書き換える。本研究では$\phi=0.1$とする。下の図は$k=99, n=500$として上記の方法でエッジを書き換えたものである。
${}$それぞれのエージェントは5つの静的な特徴量を有する。これは社会経済的な変数(変化しない)を模したものである。また、20の動的な特徴量も有する。これは意見や態度といった変化し得る変数を模したものである。単純化のためこれら2値変数とし、初期値はランダムに決定する。
それぞれのエージェントは25の特徴量のユークリッド距離で重みづけられたリンクを有する。また、初期にランダムで特徴量が決定された際のユークリッド距離の全体の平均をその期待値とし、その期待値よりも高ければポジティブ、低ければネガティブとする。以上を踏まえて、エージェント$i$と$j$の$t$時点での距離$d_{ij, t}$と重み$w_{ij,t}$は下記のように表現される。
$$
d_{ij, t} = \sqrt{\sum_{m \in S}(s_{mi} - s_{mj})^2 + \sum_{m \in O}(o_{mi,t} - o_{mj,t})^2}
$$
$$
w_{ij,t} = E(d) - d_{ij,t}
$$
${}$ここで$m$は特徴量の次元で$S$は静的な特徴量のセット、$O$は動的な特徴量のセットである。そして、$E(d)$はランダムで特徴量がアサインされた際の距離(期待値)である。
${}$本研究では「壺モデル」を使用する。仮にランダムに選択されたエージェントをエージェント$i$とする。分かりやすいように、ここでは特徴量が1つあり、それらは赤と青をとるとしよう。エージェント$i$にはいくつかのリンクで繋がった近隣エージェントがいるが、この近隣エージェントが持つ特徴量(赤or青)がエージェント$i$の「壺」に入り得る。仮に5の近隣エージェントがいて、それぞれその特徴量が[赤、赤、赤、青、青]だった場合、エージェント$i$の「壺」に[赤、赤、赤、青、青]が入るイメージである。ただし、どの近隣エージェントの特徴量も同一の確率でエージェント$i$の「壺」に入るわけではない。その確率は下記とする。
$$
p_{j,t} = \frac{|w_{ij,t}|}{\sum_{A(i,k)=1} |w_{ik,t}|}
$$
${}$ここで$A(i, k) = 1$とはエージェント$i$と$k$がリンクしていることを意味する。つまり上記は、リンクしているエージェントの重みの絶対値の合計のうち、どの程度そのエージェントの重みの絶対値が存在するかによってそのエージェントの特徴量が「壺」の中に入るかどうかが決定する。また、ここで仮にネガティブな重みを有するエージェントの特徴量が「壺」の中に入った場合、90%の確率でその特徴量が「壺」から取り除かれるか、10%の確率でその特徴量が逆の特徴量(赤なら青、青なら赤)として「壺」に入る。
このようにしてエージェント$i$の「壺」の中身が決定する。「壺」の中身が決定すれば、その「壺」の中からランダムに特徴量が選択され、それがエージェント$i$の新しい特徴量となる。
本研究ではまずエージェントがランダムに選択されて、上記のモデルにしたがって特徴量が変更されていく。それを確率的に安定するまで繰り返す。ここで確率的に安定を以下の指標で評価する。
$$
\sigma = \sum_{i,j \in N} \sum_{o \in O} w_{ij} (2|o_{i} - o_{j}| - 1)
$$
上記は全てのエージェントの組み合わせと特徴量について、その特徴量の差(今回は0or1の2値変数を考えるので、-1か+1をとる)を重みづけたものである。この指標が100万回の処理の後に続く100回の処理をした後に統計的に有意な違いが見られないときに確率的に安定したと考える。
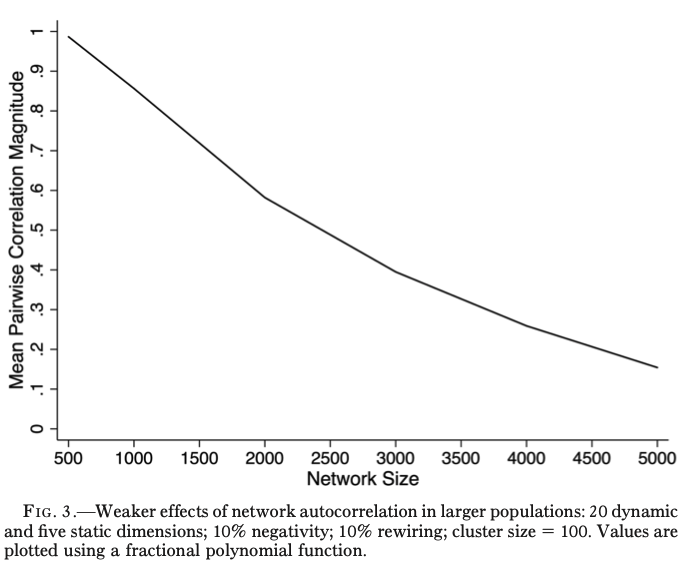
下記はエージェント数を500から5000まで増加させた時に、確率的に安定するまで上記の手順を繰り返した時の結果である。y軸方向にそれぞれの特徴量のペアの相関係数の絶対値の平均をとっている。
これを見るとわかるように、エージェントの数が多ければ特徴量の相関は低くなる傾向にある。GSSのサンプル数を考えると、この結果は上記のモデルだけでは意見の相関が説明できないことを示唆している。もちろん、処理を繰り返していけば相関が高くなるのだろうがその処理を実行するに時間がいくらあっても足りない。そこで、上記のモデルに新たな処理を加えることでGSSで確認されたような相関を導く。その処理とは下記2つが考えられる。
- エージェントの静的な特徴量に関する処理
- 高い次数を有するエージェントに関する処理
${}$「エージェントの静的な特徴量に関する処理」では確率$p$でエージェントの「壺」にある特徴量のうち静的な特徴量が自身のそれと置き換わるようにする。これは自身の静的な特徴量が時間を通してライフスタイルに影響を及ぼし続けていることを表現するような処理である。
「高い次数を有するエージェントに関する処理」では全てのエージェントと繋がったエージェントを考え、確率$p$で近隣エージェントからではなくこのエージェントからの影響を受けるとする。これはマスメディアやオピニオンリーダーといった媒体を表現している。
上記いずれの方法においても十分な相関を生み出すことが可能となった。つまり、このようなプロセスが個人のライフスタイルを説明する上で必要であることが示唆された。いずれにせよ、人々のライフスタイルを説明するにはこのようなエージェント同士の相互作用を考慮する必要がある。