論文
この記事は下記の論文の内容をまとめたものである。
Flache, A., & Macy, M. W. (2011). Small worlds and cultural polarization. The Journal of Mathematical Sociology, 35(1-3), 146-176.
概要
本研究は、意見の分極化(polarization)に対する橋渡しネットワークの効果が、エージェント同士がどのように相互作用を行うのかによって、異なることを示している研究である。エージェント同士が相互作用すると互いに類似していくということのみを考慮した場合には、橋渡しネットワークの効果はあまり見られず、いずれにせよ意見の分極化は抑えられる。一方で、エージェント同士の意見があまりに異なる場合相互作用を行うと互いにさらに異なるようになるということをも考慮した場合には、橋渡しネットワークは意見の分極化を促進する傾向にある。
背景
異なるネットワークのかたまりを結ぶようなネットワーク(以下、橋渡しネットワーク)によって文化が1つに収束していくのか、それとも多くの文化を生み出すのかは未だはっきり分かっていない。前者を予測するような研究は、橋渡しネットワークによって両者の文化が媒介され両者の文化が類似してくると予測している。一方で後者を予測するような研究は、現実世界において実際に多くの文化が存在していることを指摘している。このように、どちらが正しいのかは未だはっきりしていない。
そこで本研究ではエージェントベースモデルを使用してその問いに答えていく。特に本研究では、エージェントがどのような相互作用を起こすのかによって最終的な帰結が異なることを示す。
方法
エージェントの相互作用として2つの相互作用を考える。
1つ目はポジティブな相互作用であり、相互作用を起こすとエージェント同士が類似していくというものである。2つ目はネガティブな相互作用であり、あまりに異なるエージェント同士が相互作用した場合そのエージェントはさらに異なっていくというものである。
結果の頑強性のテストのために、ノードの数と密度(実際にノードが持つエッジの数を理論的にノードが取り得るエッジの数で除したものの平均値)を独立に操作する。また、文化の次元を変化させる。
${}$まずエージェント$i$が有する文化$k (1≦k≦K)$におけるスタンス$s_{ik}$を-1から+1をとる連続量として考える。
また$t$時点において、エージェント$i$とエージェント$j$のネットワークのウェイト$w_{ij,t}$を考える。このウェイトはエージェント$i$と$j$のスタンスが類似していれば類似しているほど高くなる。エージェントのスタンスは変化するためこのウェイトも時間経過とともに変化する。
このウェイトが正の値を取ればポジティブな相互作用を起こすとする。つまり、エージェント$i$のスタンスはエージェント$j$のスタンスに引っ張られるように作用する。逆にこのウェイトが負の値を取ればネガティブな相互作用を起こすとする。つまり、エージェント$i$のスタンスはエージェント$j$のスタンスから離れるように作用する。なお、ウェイトの絶対値が大きければポジティブな相互作用もネガティブな相互作用もその影響力が大きくなる。
ここで、ウェイトの範囲を-1から+1とすればエージェントはそのスタンスの類似度によって正の相互作用も負の相互作用も起こし得る。一方で、ウェイトの範囲を0から1にすればエージェントはその類似度に依らず常に正の相互作用を起こす。これを定式化することによってミクロレベルの相互作用を制御する。
具体的には、ウェイトの範囲を-1から+1に設定する場合$t+1$時点でのエージェント$i$とエージェント$j$のウェイト$w_{ij, t+1}$を下記とする。
$$
w_{ij, t+1} = 1 - \frac{\sum_{k=1}^{K} |s_{jk,t}-s_{ik,t}|}{K}
$$
${}$一方でウェイトの範囲を0から+1にする場合$t+1$時点でのエージェント$i$とエージェント$j$のウェイト$w_{ij, t+1}$を下記とする。
$$
w_{ij, t+1} = 1 - \frac{\sum_{k=1}^{K} |s_{jk,t}-s_{ik,t}|}{2K}
$$
${}$上記の定式化ではt時点におけるエージェント$i$と$j$の文化$k$に対するスタンスの違いが大きければ大きいほど分数部分の分子が大きくなり、結果的にそのウェイトは小さくなる。すなわち類似度が低いと判断される。それを文化の数$K$で平均化したものが上の定式化の意味である。なお、分数部分の分母を2倍するか否かによってそのウェイトが取り得る範囲を制限している。
また、相互作用の影響を下記のように定式化する。
$$
\Delta s_{ik,t} = \frac{1}{2N_{l,t}} \sum_{j≠i} w_{ij,t} (s_{jk,t} - s_{ik,t})
$$
${}$ここで$N_{l,t}$とは$t$時点でエージェント$i$が持つネットワークである。
上記の定式化の$\sum$部分では$i$から見た時の$j$との差分にウェイトを掛けている。ここでの差分方向($s_{jk,t}$方向)に$s_{ik,t}$が引っ張られる。なお、ウェイトの絶対値が大きければ大きいほど(類似度が高ければ高いほど)その引っ張られ具合が大きくなる。ここで、ウェイトが負の値をとった場合その引っ張られる方向は逆となる。すなわち、$s_{jk,t}$から離れる方向に作用する。
なお、分母の2は$\Delta s_{ik,t}$が-1から+1に収まることを保証するためのパラメータである。
上記を用いて$t+1$時点でのエージェント$i$の$k$に対するスタンス$s_{ik, t+1}$は下記の通りとなる。
$$
s_{ik,t+1} =
\begin{cases}
s_{ik, t} + \Delta s_{ik,t} (1 - s_{ik, t}) & \text{if} & s_{ik,t} > 0 \
s_{ik, t} + \Delta s_{ik,t} (1 + s_{ik, t}) & \text{if} & s_{ik,t} ≦ 0
\end{cases}
$$
この定式化により$-1≦s_{ik,t+1}≦+1$であることを保証している。
本研究の関心は異なるネットワークのかたまりが複数存在する状態に、そのかたまり間をつなぐ橋渡しネットワークが生じた場合の結果を考察することである。
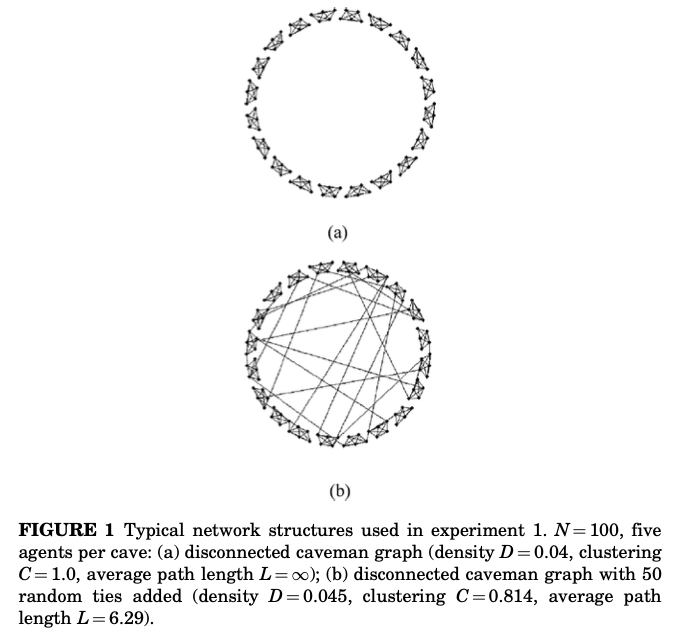
ここで下記のような2種類のネットワークを考える。
(a)は5つのノードからなる20のかたまりが存在するネットワークである。ここではローカルクラスター係数(推移性:友達Aと友達Bが友達である割合)は1である。また、平均パス長はノード同士が隔絶されているため$\infty$となる。
(b)は(a)に対してランダムに隔絶されているノードのペアを50選択してそのペアを繋げたネットワークである。結果、(b)では隔絶されたかたまりは存在しておらず、何らかのネットワークで他のかたまりと結ばれていることが見て取れる。密度はほんのわずかに上昇(.04程度)しただけであり、推移性も0.81と高いままだが平均パス長は6.29となった。もちろん、ランダムにペアを選択するので必ずしも全てのかたまりが結ばれるわけではないが、少なくとも隔絶されたかたまりは減少する。このように隔絶されたかたまりを減少させる橋渡しネットワークを導入することでその影響を考察する。
${}$なお、本研究では各ステップにおいてランダムにエージェント$i$が選択され$s_{ik,t}$と$w_{ij,t}$が更新されるが、その更新は両者のどちらか一方のみが更新される。同期的更新に対する考察は本研究のスコープの対象外であるためである。
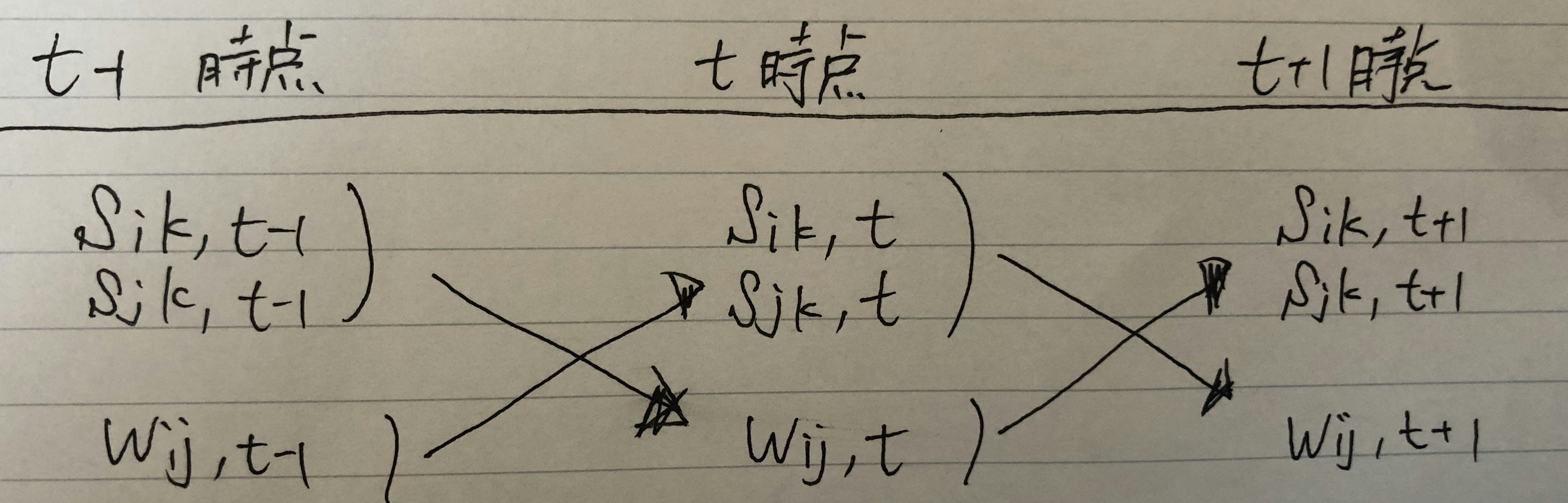
この文章は少しわかりにくいのだが、上記の式をよく見てみると下記の関係になっていることがわかる。
${}$つまり、$t-1$時点でのエージェント$i$と$j$のスタンスによって$t$時点での重み(類似度)が決定され、また$t-1$時点での重み(類似度)(と$t-1$時点でのエージェント$i$と$j$のスタンス)によって$t$時点でのスタンスが決定されるのである。よって、更新はスタンスと重み(類似度)の2つに対して行い得るのだが、ここではどちらか一方のみを更新しようと言っているのである。
${}$最後に、異なるスタンスを持つネットワークのかたまりがどの程度綺麗に形成されているのか(分極化:polarization)を捉える指標$P$を考える。まず、エージェント$i$と$j$のスタンスの違いを下記のようにその差分の絶対値(の平均)で表現する。なお、スタンスは-1から+1をとる値なので下記の最大値は+2である。また、仮に全ての$k$においてスタンスが一致すれば下記は0となる。
$$
d_{ij,t} = \frac{1}{K} \sum_{k=1}^{K} |s_{jk,t} - s_{ik,t}|
$$
${}$その上で、$t$時点での$P$、$P_t$を下記の通りに定式化する。なお。$\bar{d_t}$はすべてのノードの組み合わせにおける$d_t$の平均値である。
$$
P_t = \frac{1}{N(N-1)} \sum_{i≠j}^{i=N,j=N} {(d_{ij,t} - \bar{d_t})^2}
$$
${}$つまり、上記は全てのノードの組み合わせ(ただし、ノード$i$同士の組み合わせは除く)の$d_{ij,t}$の分散である。仮に全てのノードが全く同じスタンスを有していれば$P_t = 0$となる。また仮に$d_{ii}$のような自分自身との距離を含むとその最大値は1となる。そのような場合を除くとNが多くなるにつれて1に近づき、例えば$N=100$ならば$0.999898$となる。
結果
本研究では2つの実験をエージェントベースモデルによって実施する。ここでの中心的な課題は「スタンスの分離度合い(polarization)に対する橋渡しネットワークの影響がどのようにミクロレベルの相互作用の仕方によって異なるのか」を考察することである。
1つ目の実験では上の図(a)で示したような隔絶されたネットワークを考える。その上で橋渡しネットワークをランダムに追加していく。2つ目の実験では隣接したネットワークのかたまりのみが接続された状態において橋渡しするネットワークを追加していく。どちらの実験においても3つの頑強性テスト(ネットワークのかたまりの数とサイズを変更、密度を変更、$K$の変更)を行う。
実験1
まず上の図(a)のネットワーク(以降、隔絶ネットワーク)に、それまではつながっていなかったノード同士間に0.003の確率で新たなリンク(橋渡しネットワーク)を形成する。50回それを行うと平均で28.75の新たなリンクが形成され平均で密度が.006上昇した。もちろん、この方法で全てのネットワークのかたまりが繋がるわけではなく、平均で20個中4個のネットワークのかたまりが隔絶されたままであった。またここでは$K=2$とし各エージェントのスタンスは一様分布からの乱数で決定する。
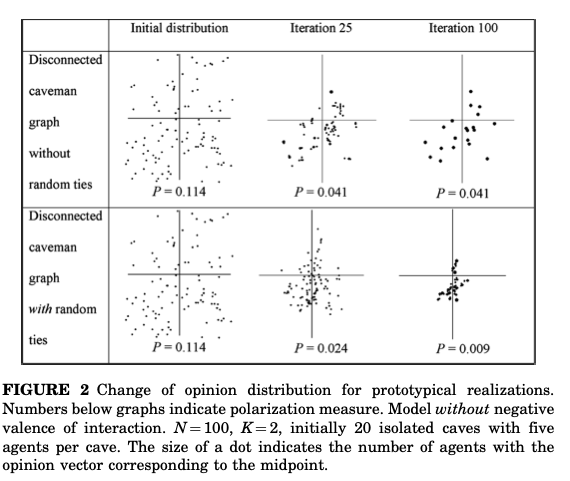
下の図は二次元上($K=2$であることに留意)に各ノードのスタンスをプロットしたものである。なお、ここではネガティブな相互作用を想定していない。図中の上は隔絶ネットワークのままシミレーションを実施したものであり、下は橋渡しネットワークを追加したものである。
図から分かるように隔絶ネットワークでは各かたまりで同一のスタンスが形成され、かたまり間のスタンスは異なったままであるが、橋渡しネットワークを加えると全体として、かたまり間のスタンスの違いが消失している。ただし、いずれにしても$P$の値は小さいのだが、橋渡しネットワークを加えた場合の方がそれは小さい。
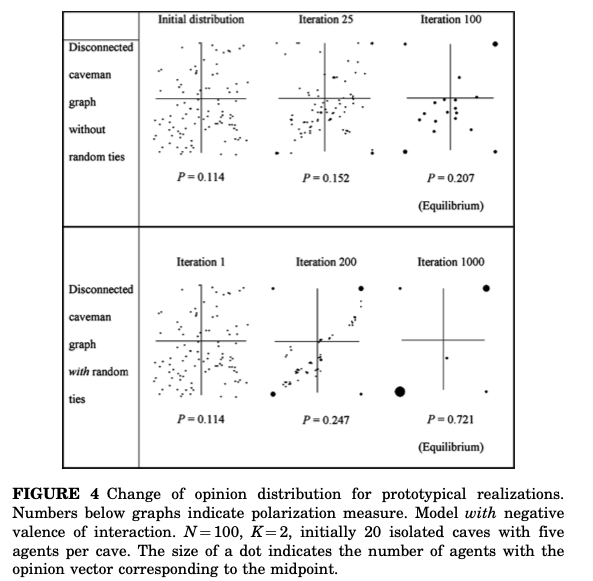
続いて、ネガティブな相互作用を取り入れる。その結果が下記の図である。
${}$まず橋渡しネットワークがない場合を見ていく。いくつかのエージェントが極端なスタンス、それもエージェント同士で全く異なるスタンスをとっていることが見て取れる。これはかたまり内でランダムにアサインされたスタンスがたまたまネガティブな相互作用を行うくらいに異なっており、相互作用を繰り返すことでさらに異なるスタンスを取るようになり、最終的には両極端なスタンスをとるようになることから生じた現象である。その結果、$P$の値も0.207と大きくなっている。
次に橋渡しネットワークを追加した場合を確認する。図からわかるように、両極端なスタンスをとるエージェントが増加していることがわかる。最終的には$P$の値は0.721となりスタンスの分極化がより進んだことが見て取れる。
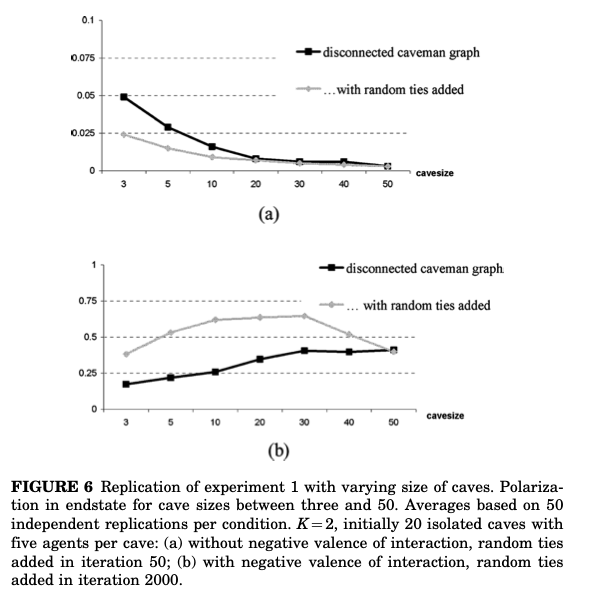
${}$ここでかたまりのサイズを変更する。なお、全体のエージェントの数$N$はかたまりの数を考慮した上で最も100に近くなるように設定した。例えば、かたまりのサイズを3に設定した場合、33個のかたまりを作成して$N$を99とし、かたまりのサイズを30とした場合は3つのかたまりを作成して$N$を90、かたまりのサイズを40とした場合は3つのかたまりを作成して$N$を120とした。
${}$結果、ポジティブな相互作用のみを考慮した場合においてかたまりのサイズが20以上の場合、隔絶ネットワークと橋渡しネットワークを加えた場合のネットワーク間で$P$の値の違いは消失した。一方でネガティブな相互作用を考慮した場合、かたまりのサイズが50の場合のみを除いて、橋渡しネットワークを加えると$P$の値が増加した。下の図はそれらの様子を表している図である。(a)がポジティブな相互作用のみを考慮した場合、(b)がネガティブな相互作用も考慮した場合である。
${}$次にかたまり内のネットワークをいくつか排除することで密度を変化させ同様の実験を実施したが、結果に変化はなかった。(ポジティブな相互作用のみを考慮して隔絶されたネットワークに橋渡しネットワークを導入すると$P$は減少し、ネガティブな相互作用も考慮して隔絶ネットワークに橋渡しネットワークを導入すると$P$は増加する)
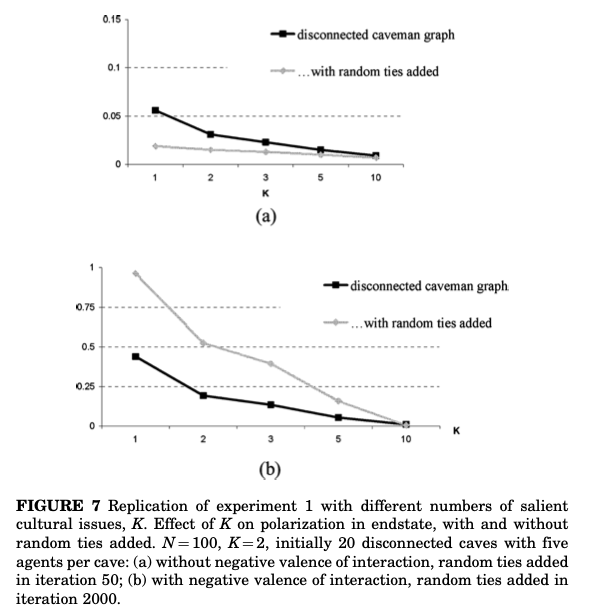
次に$K$を変更する。結果は下記の図の通りである。
${}$「ポジティブな相互作用のみを考慮して隔絶されたネットワークに橋渡しネットワークを導入すると$P$は減少し、ネガティブな相互作用も考慮して隔絶ネットワークに橋渡しネットワークを導入すると$P$は増加する」という傾向には変化ないが、$K$が大きくなるにつれてその効果は減少する。また、$K$の増加につれて$P$は減少する。
${}$以上の結果は、パタメータを変更しても概して「ポジティブな相互作用のみを考慮して隔絶されたネットワークに橋渡しネットワークを導入すると$P$は減少し、ネガティブな相互作用も考慮して隔絶ネットワークに橋渡しネットワークを導入すると$P$は増加する」という結果に変わりがないことを示している。
実験2
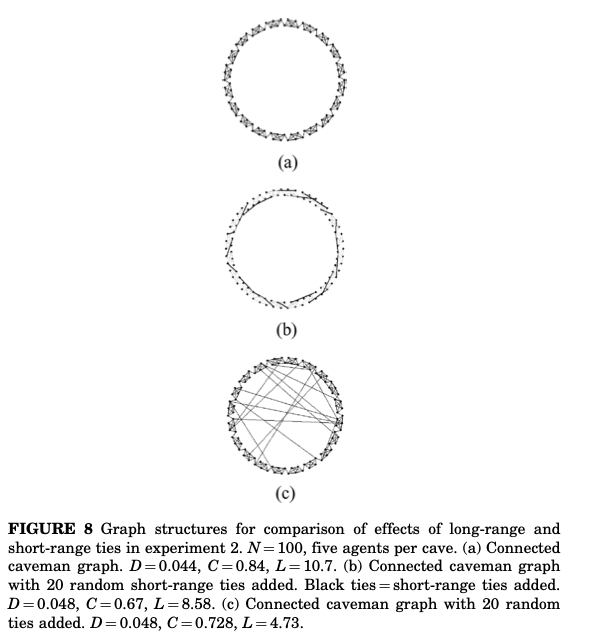
実験1の結果には2つの要因が考えられる。1つ目が橋渡しネットワークの形成によるもの、2つ目がネットワークの構造そのものの変化によるものである。そこで実験2では全てのかたまりが接続された状態から(下図の(a))隣接するかたまり同士のみの橋渡しネットワーク(以下、隣接橋渡しネットワーク)を考える(下図の(b))。また、(a)から通常の橋渡しネットワークを追加したときの場合も考える(下図の(c))。
このようにすることで(a)から(b)の際には平均パス長と推移性をあまり変化させないで済み、(b)から(c)の場合には平均パス長のみを変化させることができる。
${}$まずポジティブな相互作用のみを考慮した時を考える。結果、隣接橋渡しネットワークを加えたとしても((a)から(b))、通常の橋渡しネットワークを加えたとしても((b)から(c))$P$に変化は見られなかった。すなわち、いずれの状況においても分極化は生じずに$P$は減少する。すなわち、ポジティブな相互作用のみを考慮し、ネットワークが繋がっている状態の時には意見の分極化はいずれの状態においても減少していく。
${}$一方で、ネガティブな相互作用も考慮した場合、隣接橋渡しネットワークを加えたとしても加えなかったとしても((a)から(b))$P$は増加する。すなわち、隣接橋渡しネットーワークを加えたとしても加えなかったとしても分極化が生じて$P$は増加する。通常の橋渡しネットワークを考慮した際には((b)から(c))$P$は増加する。すなわち、ネガティブな相互作用をも考慮した際には、意見の分極化が進み、さらに橋渡しネットワークはその分極化を増幅する。
なお上記の傾向は実験1同様にかたまりのサイズや密度、$K$を変化させても変わらなかった。
つまり、ポジティブな相互作用のみを考慮した場合は橋渡しネットワークの効果はあまり見られず、いずれにせよ意見の分極化は抑えられる。一方で、ネガティブな相互作用をも考慮した場合には橋渡しネットワークは意見の分極化を増幅する傾向にある。