はじめに
ネットワーク分析系の指標とその意味、コードの備忘録である。随時更新予定。
pip installした上で下記が実行されていることを前提としている。
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
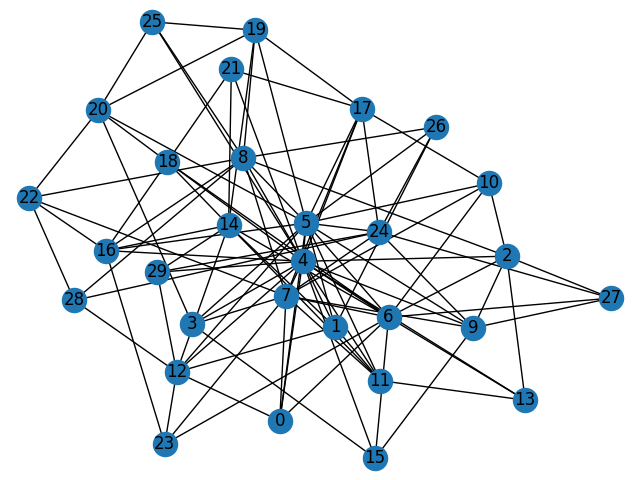
さらに下記のようなネットワークを予め用意しておく。
G = nx.barabasi_albert_graph(30, 4, seed=1234)
nx.draw(G, with_labels=True)
また、例として学校のクラス内の生徒の友人ネットワークをイメージしながら考える。上記のネットワークをクラス内の生徒の友人ネットワークを表現していると考える。なお、無向グラフを想定している。
次数
${}$あるノードが持つエッジの数。クラスにいる生徒$i$の持つ友人の数。以降では、ノード$i$の次数を$k_i$とする。下記を実行することで辞書型で次数をとれる。
nx.degree(G)
# OUTPUT: DegreeView({0: 5, 1: 6, 2: 7, 3: 5, 4: 19, 5: 16, 6: 12, 7: 12, 8: 10, 9: 7, 10: 5, 11: 6, 12: 8, 13: 4, 14: 9, 15: 4, 16: 7, 17: 7, 18: 6, 19: 6, 20: 6, 21: 4, 22: 5, 23: 4, 24: 8, 25: 4, 26: 4, 27: 4, 28: 4, 29: 4})
平均次数
ネットワーク内のノードが持つエッジの平均値。クラスにいる生徒は平均して何人の友人がいるかを意味する。
$$
\frac{1}{N} \sum_{i}^{N} k_i
$$
degree = list(dict(nx.degree(G)).values())
np.mean(degree)
# OUTPUT: 6.933333333333334
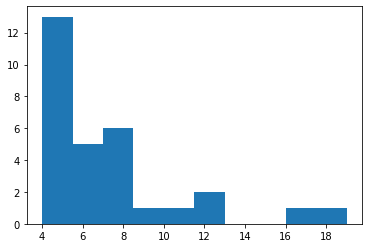
次数分布
次数の分布。クラスにいる生徒が持つ友人数のヒストグラムである。
degree = list(dict(nx.degree(G)).values())
fig, ax = plt.subplots()
ax.hist(degree)
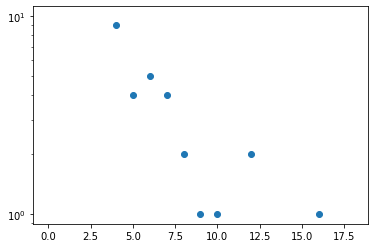
なお、両対数分布をとった時に直線的になる場合、スケールフリー性があるという。スケールフリー性とはあるノードにエッジが集中し、多くのノードはさほどエッジを持たない様を指す。すなわち、クラスには友人を多く持つ人気者が少数おり、友人をあまり持たない者が大多数である場合である。
degree = list(dict(nx.degree(G)).values())
x = [i for i in range(max(degree))]
y = [degree.count(i) for i in x]
fig, ax = plt.subplots()
ax.scatter(x, y)
ax.set_yscale('log')
ax.set_yscale('log')
リンク密度
全てのノード同士間にエッジが存在した場合に比べて、実際にどの程度エッジが存在するか。クラスにいる生徒同士のつながりの濃さを意味する。この指標は0~1をとる。ここではエッジの数を$E$とする。
$$
\frac{エッジの数}{最大取り得るエッジの数} = \frac{E}{\frac{N(N - 1)}{2}}
$$
E = G.number_of_edges()
N = G.number_of_nodes()
(2*E) / (N*(N-1))
# OUTPUT: 0.23908045977011494
最短経路長
${}$あるノードから別のノードまで到達するために通過するエッジの数の最小値である。生徒$i$から生徒$j$まで辿るのに何人の生徒を経由する必要があるかである。なお、ネットワークが分断している場合それは計測されない(論文によっては$\infty$としている)。
nx.shortest_path_length(G, source=0, target=1) # ノード0から1への最短経路長
# OUTPUT: 2
ここでノード$i$と他のノード全てのノードとの最短経路長の平均は平均最短経路長である。
shortest_path = []
i = 0 # ノード0の平均最短経路長
for j in nx.shortest_path(G)[i].keys():
if i != j:
shortest_path.append(nx.shortest_path_length(G, source=i, target=j))
np.mean(shortest_path)
# OUTPUT: 1.8275862068965518
さらに全てのノードの平均最短経路長の平均をネットワークの平均経路長と呼ぶ。
nx.average_shortest_path_length(G)
# OUTPUT: 1.8620689655172413
クラスタ係数
${}$「あるノードについてその隣接ノード同士の間にエッジが存在している割合」の全てのノードにおける平均値。生徒$i$の友人の生徒$j$と生徒$k$が友人である確率の平均値とも考えられる。つまり友人の友人は友人かどうかをあわわす指標である。E_{i}をノード$i$の隣接ノード間に存在するリンクの数とする。0~1をとる。
$$
C_{i} = \frac{E_{i}}{\frac{k_i(k_i - 1)}{2}}
$$
$$
C = \frac{1}{N} \sum_{i=1}^{N} C_{i}
$$
nx.average_clustering(G)
# OUTPUT: 0.3616497050707577
なお、上記のリンク密度はネットワーク全体をスコープとした密度であり、クラスタ係数は局所的な密度と捉えることができる。
同類選択性
同類選択性は次数の相関を表現する指標である。次数が高いノード同士(あるいは低いノード同士)がエッジで結ばれていた場合、同類選択性は高くなる。通常の相関係数と同様に-1から+1をとる。友人の多い人気のある生徒同士が友人関係にあり、友人の少ない人気のない生徒同士が友人関係にあるとき同類選択性が高くなると言える。
nx.degree_assortativity_coefficient(G)
# OUTPUT: -0.2178566111571916
中心性
更新予定。