論文
この記事は下記の論文の内容をまとめたものである。
Overgoor, J., & Adamic, L. A. (2020, May). The Structure of US College Networks on Facebook. In Proceedings of the International AAAI Conference on Web and Social Media (Vol. 14, pp. 499-510).
概要
大学生活におけるネットワークはその後の人生において重要だと考えられる一方で、大学生のネットワークを研究する際には常に大規模なデータがないというデータの不足が問題としてあった。そこで、本研究ではFacebookの大規模なデータを用いて記述的・探索的に大学生のネットワークを調べている。
背景
大学生活におけるネットワークに関する研究において、homofily(似たもの同士がネットワークを結ぶ現象)やpropinquity(地理的に隣接している者同士がネットワークを結ぶ現象)といった現象が研究の対象となってきた。しかしながら、大学生活におけるネットワークに関するcomprehensiveなデータを集めることは困難であるため、そのスコープが限定されていた(高校生のcomrehensiveなデータは存在している)。本研究ではcomprehensiveなFacebookのデータを用いて記述的な分析を行う。
データ
本研究に用いるデータはFacebookから収集したものである。それに加えて、大学に関する情報も取得した。
前者についてはまず、Facebook ユーザーがプロフィール上で自己申告している年齢、出身地、学歴、卒業年、専攻、大学の場所を変数として用いる。学歴については、その学校名が現実に存在し、そのユーザーのFacebook上の友達のうち10人以上の友達が同じ学校に通っていたならば信頼できると判断した。また、出身地が掲載されていな場合、高校の場所をそのユーザーの出身地とした。
また、Facebook上の友達関係をネットワークとする。もちろん、Facebook上の友達関係が必ずしもオフラインの友達関係を表現しているとは限らないが、大学生活という文脈においては、多くのエッジが新学期の最初に形成されていることを考えればある程度オフライン上のネットワークを反映していると考えられる。
後者についてはU.S. Department of Educationが公開しているデータ等を用いる。本研究では、平均100人以上の入学者がいるpublicとprivate(non-profit)な大学に的を絞る。また、College Scorecard(大学ランキング的なやつ)に2008-2015年の間に少なくとも4年以上掲載されている大学に的を絞る。ここで公開されているデータにおいて欠損値があった場合は平均値で補完している。また、大学院のみをもつ大学は除外した。
ここでの変数は、大学合格率、卒業率、学校タイプ(public/private)、マイノリティーグループ(黒人系、ヒスパニック系、女子大)、宗教、ドミトリーの存在(学生の50%以上を収容できるキャパシティがある)である。なお、当該大学にマッチするFacebookユーザーが、100人未満の場合とアメリカ人のユーザーが50%未満の大学は分析から排除した。
最後に同じ大学に通っていても何年度入学者であるかで状況は異なるので、それを考慮した(それをclassと呼んでいる)。18%しかいつ卒業したのかをプロフィールに載せていなかったので勾配ブースティングによって推定した。すなわち、プロフィールにいつ卒業したのかを掲載した者を使ってモデルを訓練し、掲載していない者についてそれを予測した。
使用した特徴量は、ユーザー個人(年齢等)、友達作りのタイミング(同大学内のユーザーと友達になった数が最も多い月等)、そのユーザーの大学に関する変数である。
訓練したモデルで予測される確率が0.75以上の者のみを分析の対象とした。
また、同一class内で最も新しい友人関係が形成された週をそのclassの開始年とした。
さらに、学校レベルの変数としてGreek life(大学全体規模のギリシア系の集まり…?)を考える。ここでは、同一大学から少なくとも75%以上の者が参加しているFacebook groupを見つけ、グループ名にギリシア文字が入っている場合、それをGreek groupsとした。
また、公開されている大学データと上記のステップで作成されたclassのデータの人数を比較した。その際、classのデータの人数が公開されている大学データの0.5~1.25倍以外の場合そのclassデータは信頼できないとしてを分析から除外した。
データの記述的特性
最終的に、7,660のclass、1,159の大学、約760万人が分析の対象となった。同一class内でエッジは2億3250万存在する。同一の大学で異なるclass間には3億2010万のエッジが存在する。異なる大学同士では7億5650万のエッジが存在する。
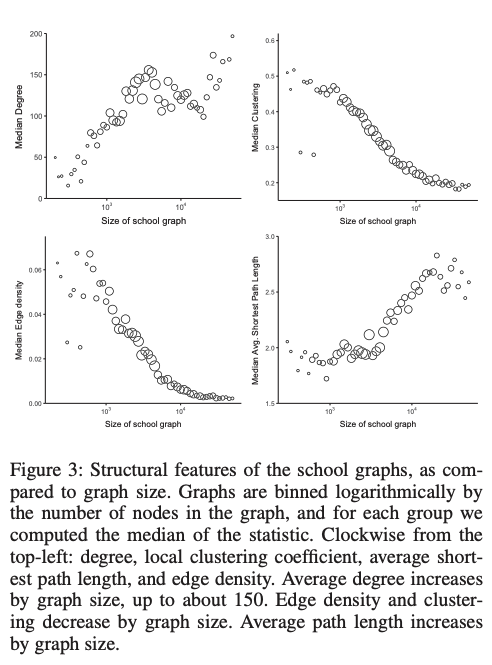
下図はx軸に大学のグラフの大きさ(ノードの数)をとり、y軸にいくつかのネットワークの特徴量(次数、クラスタ係数、エッジ密度、平均最短パス長)について、その大学に該当するユーザーの中央値をとったものである。ここで確認できる関係性は先行研究のそれと整合的であった。
また学校同士でネットワークの形態に違いが見られた。例えば、小さなprivateなliberal-arts大学は同一class内での友人関係の割合が、同等サイズのpublicな大学よりも高い。下図はFruchterman–
Reingold projection法(ネットワークを近似的に可視化)によって、private大学とpublic大学のネットワークを可視化したものである。ここからわかるように、private大学の方がclass間の重なりが少ない。
またmodularity score Q(コミュニティを切り出す方法で高ければそれだけコミュニティが切り出されている)はprivate大学において0.309、public大学は0.133であった。
グラフの類似度としての異なり度合い
本研究ではグラフ同士の違いを機械学習(ランダムフォレスト)による予測の難しさとして考える。すなわち、あるグラフとあるグラフのclassifier問題を考え、予測が難しければそれらの類似度が低いと考える。ここではAUCをその類似度と捉える。AUCが高ければ簡単に区別がつくため類似度が低く(異なり度合いが大きい)、AUCが低ければ区別が困難なため類似度が高い(異なり度合いが小さい)と捉えることができる。
まず、それぞれのclassのグラフから250のノード(エゴノードと呼ぶ)とそのノードと直接リンクしている同一大学内のノードを復元抽出でランダムサンプルする。なお、大学開始年から4年間継続したエッジしか考慮に入れない。このサンプリングデータにおいて、以下の特徴量を考える。
- ノード数
- 次数分布の平均と分散
- 次数密度
- サンプリングされたエゴノードと同一学年のノードの割合
- 同類度(degree assortivity)
- 代数的連結度(algebraic assortivity)
- クラスタ係数
- modularity of the modularity-maximizing partition
- eigenvector and betweenness centralization
- number of connected components of k-Cores and k-Brace
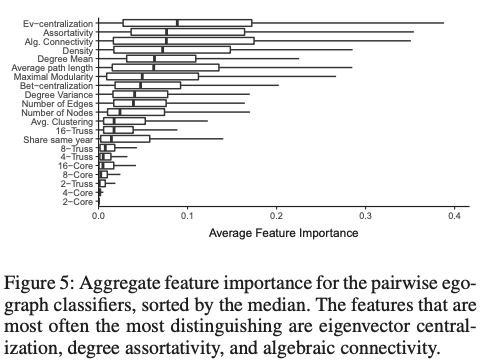
それぞれのペア(例えば、2010年度入学のA大学vs2010年度入学のB大学)においてランダムフォレストを訓練させる。feature importanceの平均をプロットしたものが下図である。
学校レベルの変数によるグラフの類似度
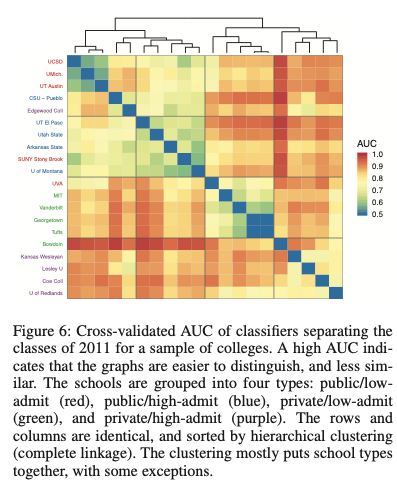
いくつかのサンプル(2011年度のclass、20の大学)のAUCの結果を階層的クラスタリングした結果が下の図である。
概して、選抜度の高いPrivateな大学同士の類似度が、その他のカテゴリに属するグループ内の類似度よりも低い。これは多種多様な学生が選抜度の高いPrivateな大学に集まっているからだと考えられる。
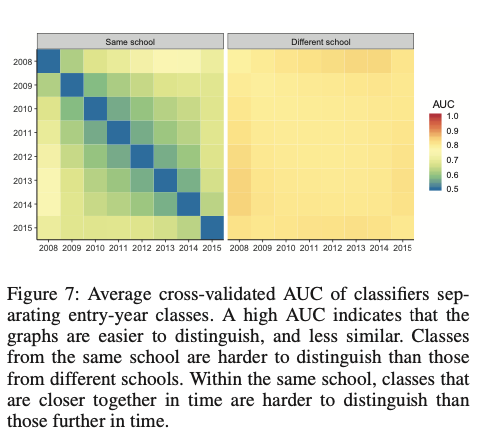
下の図はclassごとの違いを同一大学内(左)と異なる大学同士(右)でプロットしたものである。ここからわかるように、同一大学内のAUCは低く(類似度が高く)、異なる大学内のAUCは高い(類似度が低い)。また、同一大学内において年を経ることに類似度が低くなっている。
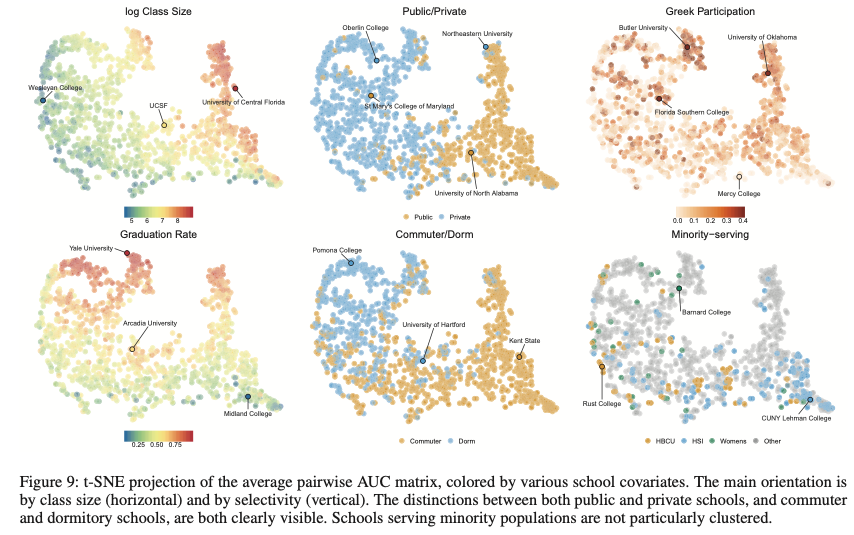
次に、同一の大学からのclassサンプルを一緒くたにして、大学同士で比較していく。大学同士のAUCの行列を考え、それをt-SNEで二次元に可視化した結果が下図である。なお、いくつかの変数で色分けしている。
ここからいくつかのパターンが見て取れる。まずclassサイズで色分けすると(左上)、x軸方向に分割できる。また、ここでは提示していないが選抜度合い(卒業率と大学合格率)で色分けするとy軸方向に分割できた。その他の変数は図の通りカテゴリカルに分割できている。
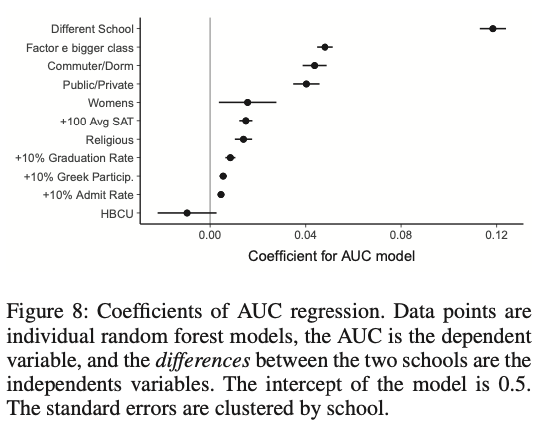
最後に、AUCを従属変数とした線形回帰を行なった(データはそれぞれのランダムフォレストの結果である。少し分かりにくいが、A大学とB大学のランダムフォレストの結果(AUC)を1行にし、A大学とB大学の違いを独立変数化している。質的変数の場合はA大学とB大学が同じなら1、異なれば0。連続変数の場合は差の絶対値)。これによって、どのような学校の違いがAUC(類似度)に貢献しているかを確認できる。
これを見ると「異なる大学かどうか」という独立変数が最も回帰係数が大きいのは当たり前だが、それに次いでclassサイズ、ドミトリーの存在、public/privateの回帰係数が大きい。
ネットワーク構造のモデリング
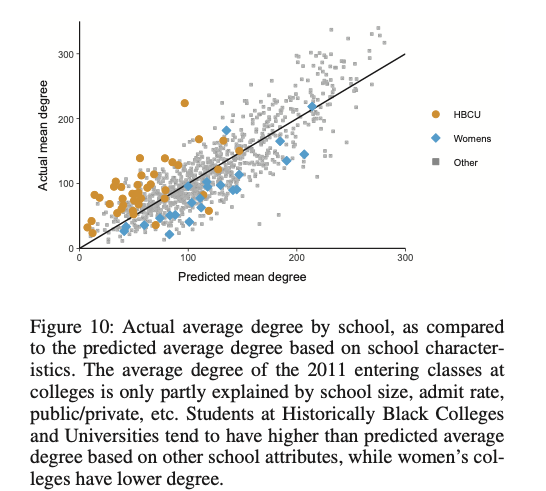
続いて学校のネットワーク特徴量の違いがどのような要因によって説明できるのかを考える。まず、黒人系大学(HBCU)かどうかと、女子大学かどうか以外の変数を用いて、従属変数を平均次数とした回帰を行なった。そのモデルによって予測される平均次数と実際の次数をプロットしたものが下図である。
なお、独立変数には使用しなかった黒人系大学(HBCU)かどうかと女子大学かどうかで色を分けている。これを見ると、女子大学かどうかは予測されるよりも平均次数が少ない。これは男性との関係を大学の外で結んでいるからだと考えられる。一方で黒人系大学の場合予測されるよりも次数が多くなっている。
続いて学校のネットワーク特徴量の違いがどのような要因によって説明できるのかを考える。
ここでは、それぞれのclassについて大学が始まった4年後までをその大学のネットワークの形態として、平均次数(log)、次数のジニ係数、クラスタ係数、年度のホモフィリー、性別のホモフィリー、出身地のホモフィリーを計算し、それらを従属変数とした回帰モデルを考える。
結果は下記の通りである。
まず次数を従属変数とした場合を見ていく。classの大きさが大きい場合、次数も大きくなる。これはclassが大きい分友人になる人数も多くなるためだと思われる。次に、卒業率が高ければ(低ければ)次数も高い(低い)傾向が見て取れる。これはすぐに卒業せずに途中で大学を去るために友人を作る時間がないためだと考えられる。またドミトリーを有していなければ次数が低い。これはドミトリーを有していればそれだけ友達を作る機会が多いためだと考えられる。private大学、HBCUの大学、Greekの参加率が高い大学も次数が高い。一方で女子大学の場合次数が少ない。これは男性との関係が大学の外で結ばれるためだからだと考えられる。
続いて次数のジニ係数(不平等の度合い)を従属変数とした場合を見ていく。classが大きい場合、ドミトリーを有していない場合、Greekの参加率が高い大学のジニ係数が高い。卒業率が高い場合ジニ係数は小さい。
続いて、クラスタ係数を従属変数とした場合の結果を確認する。classサイズが大きい場合クラスタ係数は小さい(なお、図には掲載していないがここでは次数をコントロール変数として投入している)。private大学やGreekの参加率が高い場合にクラスタ係数は高い。この背景には、このような大学には大学内でのmeeting pointsが多いことがあると考えられる。
最後にホモフィリーを従属変数とした場合を考える。全体としてホモフィリーについては、大きく選抜度が高いprivateな大学あるいはHBCUの大学で高い傾向にある。
年度のホモフィリーに関しては、Greekの参加率が高ければ年度のホモフィリーが弱まるが、これはGreekが年度を超えた交流の場であるためだと考えられる。また、ドミトリーを持たない大学もホモフィリーが弱まる。性別のホモフィリーについては逆で、Greekの参加率が高ければホモフィリーが強まる。この背景にはGreekの性別が単一化していることがあると思われる。居住地のホモフィリーについては、他のホモフィリーの傾向とは異なって選抜度が高いと居住地のホモフィリーが弱まる傾向にある。これは選抜度が低い大学にはlocalな生徒が集まりやすい傾向にあるからだと考えられる。