クォータニオンの定義や使い方については調べればいくらでも出てくるのですが、個人的には意外と重要と思っている事でもまったく説明されていないことがよくあります。これらの知識があるのとないのとではクォータニオンに対する理解度がかなり変わってくると思うため、ここにまとめておきます。
ある条件下ではクォータニオンの乗法についての交換法則が成り立つ
クォータニオンは乗法についての交換法則が成り立たないため、乗算の順序を入れ替えてはいけないとよく説明されます。しかし、実はある条件下では乗法についての交換法則が成立します。
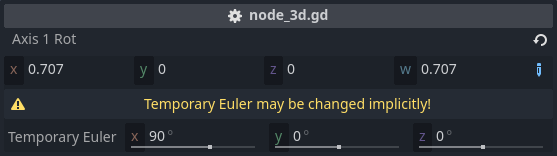
ある条件下というのは『1軸のみ回転させる場合』です。
この時、クォータニオンは『1つの実部 w』と『3つある虚部 x, y, z の内の1つ』のみを利用します。結果として2つの元しか利用しないため、二次元平面における複素数を利用した回転を行なっているのと同じ状態になります。
二次元平面における回転に順序問題は発生しない(複素数は乗法についての交換法則が成り立つ)ため、この条件下ではクォータニオンの乗算の順序をいくら入れかえても結果は同じになります。
クォータニオンの乗算の順序における回転の『先』や『後』とは
クォータニオンの乗算の順序によって回転が『先』だとか『後』だとかという説明をよくされますが、結局それが何なのかいまひとつピンとこないという人をたまに見かけます。
これは恐らく『回転』と説明された時に『グローバル回転』と『ローカル回転』のどちらかが明記されてないのが原因だと思います。
クォータニオンは基本的に『ローカル回転』を行ないます。強いていえば、一番左のクォータニオンは『初期状態からのローカル回転』であるため『グローバル回転』と等しくなりますが、それ以降は順にローカル回転を行ないます。なので、クォータニオンを操作する場合には、それらを 3D オブジェクトの親子関係のように解釈すると分かりやすいです。
例えば、
Q = Q1 * Q2 * Q3
という操作があるとしましょう。
ここでワールド(グローバル空間)に3層に親子付けされた仮想的なオブジェクトを配置することを想像します。
ワールド(グローバル空間)
└オブジェクトA
└オブジェクトB
└オブジェクトC
これらのオブジェクトは全て初期状態(全く回転していない状態)とします。
式を左から順に見ると、
- オブジェクトAを Q1 だけローカル回転
- オブジェクトBを Q2 だけローカル回転
- オブジェクトCを Q3 だけローカル回転
となり、最終的に『グローバル空間から見たオブジェクトCの向いた方向』が『3つのクォータニオンの乗算結果』というように考えることができます。つまり右にあるクォータニオンは、その左までの回転を行なった親オブジェクトの子としてローカル回転を行なっているというような感覚です。
この考え方を踏まえると、
- 『先』に回転させるというのは『親オブジェクトをローカル回転する』
- 『後』に回転させるというのは『子オブジェクトをローカル回転する』
というような解釈をすることができます。
そうして見ると、クォータニオンの計算の一番左端には常に初期状態(グローバル空間)を表わすものとして単位クォータニオンが隠れているというような考え方もできたりします。
Q = Quaternion(0, 0, 0, 1) * Q1 * Q2 * Q3
クォータニオンは常に正義という訳ではない
クォータニオンがなぜ必要なのかについて、ジンバルロックがよく挙げられます。ジンバルロックについての説明は、個人的に以下の記事が感覚的に最も分かりやすかったためリンクさせて頂きます。
要するに、オイラー角の合成による回転は、全ての状態について線形補間ができることが保証できないことにより、オイラー角のまま線形補間を行なうと最短経路ではない回転が発生する(逆に最短経路を計算するとオイラー角の数値が線形補間にならない)ということです。
これを体験するには、『3D でモーションを作成する時、オイラー角のキーフレームの補間によって最短経路での回転を手動で作成できるかどうか』を試みるのがよいでしょう。3軸の回転を使ったポーズ同士を補間しようとした時に、無理が生じるケースが出てくるはずです。
ではクォータニオンは補間において常に必要なのでしょうか。
実は、LookAt や姿勢制御、ヒンジジョイントのような『いずれかの軸を固定する(2軸までしか回転させない)』というケースにおいては、回転結果を計算する過程においてオイラー角による回転を利用する方が理にかなっていることがあります。クォータニオンが常に正義という訳ではないのです。
ちなみに Godot で姿勢制御を行う関数には、
PathFollow3D.correct_posture(transform: Transform3D, rotation_mode: RotationMode)
というものがあり、Transfrom3D を突っこむと第二引数で指定した RotationMode における姿勢制御の結果が返却されます。
補間において最短経路ではないが回転方向を制御したい場合
クォータニオンは言ってしまえば、回転軸が固定されていない時に最短経路での補間を行なうためのツールです。
ここでキャラクターモデルのポーズを補間することを考えてみましょう。『ハイキック』から『バレエのアラベスク』のようなポーズに遷移する時、股関節はどちらの方向へ回転させるべきでしょうか?
このようなケースでは、体を貫通するような補間は避ける必要がある事に気がつくと思います。
クォータニオンを補間する際、任意で最短でない方向への回転を行なう方法で最も簡単なのは『回転を避けたい方向とは真逆の方向を向いたクォータニオン』すなわち『補間の基準となる方向(補間を優先する方向)を向いたクォータニオン』を用意することです。
Q1 と Q2 というクォータニオンを補間するとき、Qp を優先させた補間を t (0 → 1) だけ行なう場合、実際の処理は以下のようになります。
Qi = Quaternion(0, 0, 0, 1)
Q = Qp * Qi.slerp(Qp.inverse() * Q1, 1 - t) * Qi.slerp(Qp.inverse() * Q2, t)
これは、『Qp』に『Q1 と Q2 から Qp の回転を打ち消した回転』を『それぞれの重みだけ乗算する』という操作を行なっています。
補間の基準となる初期ポーズ(レスト)
では補間の基準となる方向を向いたクォータニオンはどのように設定すべきなのでしょうか?
これは『モデルの初期ポーズ(Godot においては bone rest)』として設定すべきなのですが、正しくモデルをエクスポート・インポートしている限り、これは知らない間に設定されていると思われます。もし、ゲームエンジンのリターゲット機能を利用しているのであればそこで暗黙的に設定されている筈です。
補間を優先する方向として最も適切なのは可動域の中間なのですが、この条件をほぼ完全に満たすポーズは Unity Humanoid のバイクポーズになります。
引用:https://docs.unity3d.com/Manual/MuscleDefinitions.html
ただし、それほど厳密でなくとも体内への貫通は防ぐことができるため、T-pose や A-stance でも十分です。
ちなみにリターゲットを利用しないような環境においては、エクスポート時の設定によって初期ポーズが変化しうる事について注意してください。
例えば、ブレンダーからエクスポートする glTF モデルの初期ポーズは Edit Mode の時のポーズですが、Edit Mode が変なポーズの状態で Pose Mode で T-pose をさせたものをエクスポートし、リターゲットも利用しないとなれば、ポーズの遷移時に体を貫通する補間が発生する可能性が十分にあります。
補足説明
Qi = Quaternion(0, 0, 0, 1)
Q = Qp * Qi.slerp(Qp.inverse() * Q1, 1 - t) * Qi.slerp(Qp.inverse() * Q2, t)
上記の式は初期ポーズが定まっている場合、どのようなポーズ間でも利用できますが、単純に slerp を用いて2つの回転を補間するのとは結果が異なります。この方法の優れている点は、『3つ以上のポーズを補間した場合でも破綻が生じない』ことです。
他に最短でない回転を行なうために考えられる方法としては、回転させたくない方向への回転が発生しそうな時に -1 を乗算した逆位相のクォータニオンを利用するという方法があります。ただし、『回転させたくない方向であるかどうかの判断』のための『基準となるクォータニオン』がどのみち必要であり、また2つの回転同士を直接補間するので、3つ以上の回転を補間する場合において破綻が発生する可能性があります。
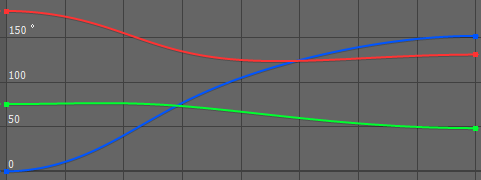
以下は2つの回転を直接 slerp で補間する場合、ブレンド結果を更にブレンドすると最短経路の取得タイミングに依存して、補間結果に破綻(値飛び)が発生する事を説明するアニメーションです。
animation1 と animation2 のブレンド結果 blend1 を animation3 と 50% ブレンドする場合、animation1 と animation2 のブレンド量の変化により blend1 と animation3 の最短経路が突然変化するため、最終的な結果に望ましくない状態遷移が発生することが分かると思います。
補間の基準となる初期ポーズに重み付けを行なった回転を乗算する方法においては、基準となる初期ポーズから 180 度以上回転する方向へ向かうような補間が行なわれないため、ブレンドを重ねた場合に値飛びの問題は発生しません。
このことから、アニメーションのブレンドのような『3つ以上の回転の補間が発生しうる』用途においては『補間の基準となる初期ポーズに重み付けを行なった回転を乗算する』という方法を採用するのが理にかなっていると考えています。
ちなみに、この最短経路の取得タイミングに依存した値飛びの問題は二次元平面上でも発生するため、Spine などの 2D ソフト等においてもどこかのタイミングで基準となる角度を設定して、最短ではないが意図しない方向への補間を防ぐという方法を取っているようです。