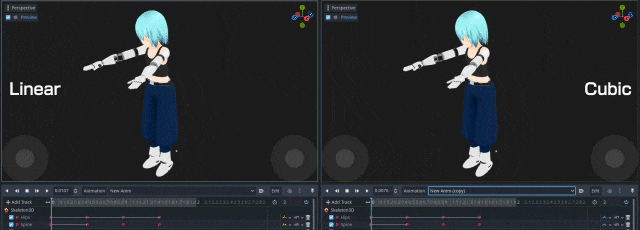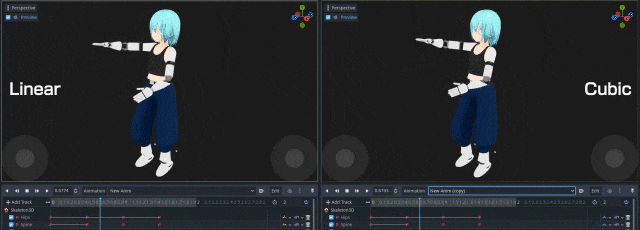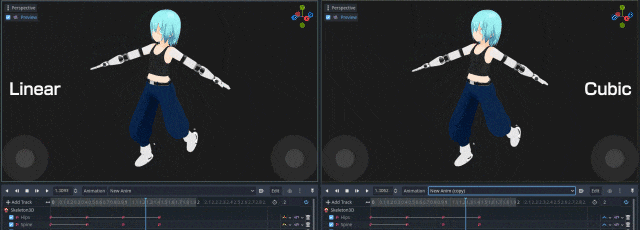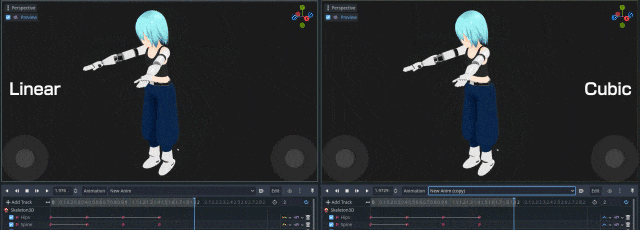
前説
世間はクリスマスの『ク』ということでクォータニオンのお話です。
この実装について完璧に解説できる自信はないのですが、タイトル通り『Exponential Map を用いてクォータニオンの Cubic 補間をする』ための情報がインターネットのどこを探しても実用的なコードとして存在しなかったので、誰かの参考になることを願いつつ、ここに備忘録として書き留める事にしました。
Godot のアニメーションにはいくつかオプションがあり、そこで補間方法として線形補間や Cubic 補間を選ぶことができます。
Cubic 補間とは、現在(from)と次(to)の2点だけでなくその前後の点も考慮した計算を行い、なめらかな動きを実現する補間方法です。Cubic 補間にも色々ありますが、Godot においては pre, from, to, post からなる4点を用いて計算を行います。
クォータニオンの Cubic 補間ができると何が嬉しいのでしょうか? 例えば、少ない点で滑らかな動きを生成する事ができます。
Godot 3 の時点ではクォータニオンの Cubic 補間が完全に壊れていました。元のコードを見てみましょう。
//the only way to do slerp :|
real_t t2 = (1.0f - p_weight) * p_weight * 2;
Quaternion sp = this->slerp(p_b, p_weight);
Quaternion sq = p_pre_a.slerpni(p_post_b, p_weight);
return sp.slerpni(sq, t2);
なるほど、『from クォータニオンと to クォータニオンの球面線型補間結果』と『pre クォータニオンと post クォータニオンの球面線型補間結果』を更に補間しているようです。
確かに Cubic 補間はいくつかの線形補間を重ねているというような考え方ができますが(参考: Barry and Goldman's pyramidal formulation)、まあこの Godot の補間式は Cubic 補間としては間違っていると言えます。ちなみにこれは「ちゃんと動いてないけどないよりマシ」という意図で Squad 補間として実装されたものだそうです。
クォータニオンの補間方法
クォータニオンの補間方法はいくつか考えられます。
角度比を用いた球面線形補間
最も代表的なのが角度比を用いた球面線形補間でしょう。正確な補間ができますが、そのままでは一般的な Cubic 補間の式と互換性がないという問題があります。うまく Barry-Goldman の式に落とし込めれば Cubic 補間もできそうな気がしなくもないですが、今回は別の方法を使います。
クォータニオンの各要素を直接補間して後で正規化する
実はこれもそこそこの補間が可能で、ものによっては nlerp という名前で実装されていることがあります。しかし、この方法を用いてクォータニオンの要素を線形補間したとしても、球面線型補間にはならないという問題があります。ただし、回転が十分に小さい場合には影響が殆ど視覚的に表れないため、そういった特殊なケースで計算コストを減らす為にこの直接補間を用いるケースがあるようです。
Exponential Map を用いた補間
最終的に Godot 4 に実装したのがこの Exponential Map を用いた Cubic 補間です。クォータニオンにはなんやかんやあって指数と対数が定義できますが、僕は数学の専門家ではないので他のサイトに解説を任せます。
要約すると、2つのクォータニオンの対数をとり、それらを線形補間して指数をとると多少の誤差はあるけど球面線型補間ができているという事です。今回重要なのは、この誤差についてどう処理すべきかということになります。
Exponential Map を用いた補間は、回転するごとに誤差が生じます。以下の記事の中程にある GIF 付きの解説が分かりやすいでしょう。
ではその誤差がどこで問題になるのでしょうか。実際に Exponential Map を用いた補間を実装してみましょう。
Exponential Map によるクォータニオンの Cubic 補間の実装
テストプロジェクトには GNSS-Stylist 氏のサンプルプロジェクトのミラーを利用させて貰います。
前処理
Exponential Map を利用する前に、それぞれのクォータニオンが最短経路を選択するように前処理を行う必要があります。
まずはクォータニオンの位相を揃えます。いくつかリサーチした所、クォータニオンの W 要素が常に正になるようにするという手法があるようですが、Godot 上だとうまくいかなかったので、毎回 Basis からの変換を通す事で位相を揃えるようにします。
Quaternion from_q = *this;
Quaternion pre_q = p_pre_a;
Quaternion to_q = p_b;
Quaternion post_q = p_post_b;
// Align flip phases.
from_q = Basis(from_q).get_rotation_quaternion();
pre_q = Basis(pre_q).get_rotation_quaternion();
to_q = Basis(to_q).get_rotation_quaternion();
post_q = Basis(post_q).get_rotation_quaternion();
次に各クォータニオンが一つ前のクォータニオンから近い回転となるように、それらをフリップさせます。
// Flip quaternions to shortest path if necessary.
bool flip1 = signbit(from_q.dot(pre_q));
pre_q = flip1 ? -pre_q : pre_q;
bool flip2 = signbit(from_q.dot(to_q));
to_q = flip2 ? -to_q : to_q;
bool flip3 = flip2 ? to_q.dot(post_q) <= 0 : signbit(to_q.dot(post_q));
post_q = flip3 ? -post_q : post_q;
これで前処理が完了しました。
実装1(特別な処理を施さずに対数空間で Cubic 補間を行う)
まずは単純に各クォータニオンを対数空間に持っていき、補間して指数をとってみましょう。
Quaternion ln_from = from_q.log();
Quaternion ln_to = to_q.log();
Quaternion ln_pre = pre_q.log();
Quaternion ln_post = post_q.log();
Quaternion ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
return ln.exp();
対数クォータニオンについては積の交換法則が成り立つため、もし Cubic 補間を行う関数があれば、それをそのまま適用することができます。
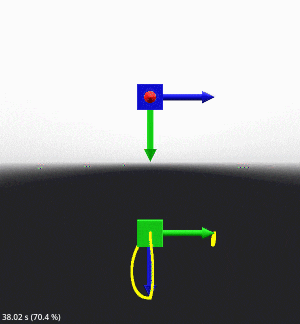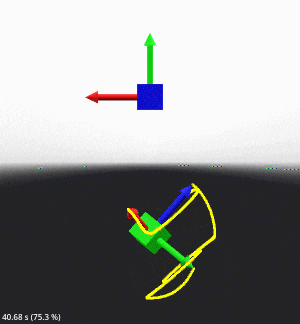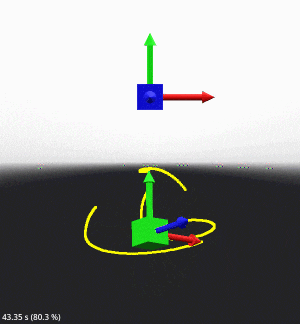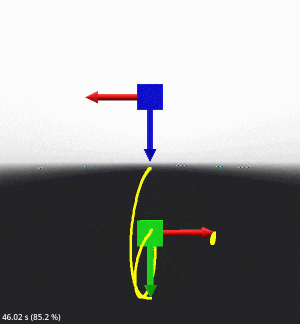
結果は以下のようになります。
ある程度うまく動いているようですが、Cubic 補間ではありえないキックバックのような動きが発生しています。
また、回転軸が安定していないようです。これは例えば 45 度傾むけたオブジェクトを 90 度回転させると一目で問題が分かります。
どうやら from クォータニオンをそのまま対数空間に持っていくと、補間の開始時点で初期クォータニオンから from クォータニオンまでの誤差が発生してしまい、そこからさらに回転を行うので誤差がかなり大きくなってしまうようです。
とりあえず、『初期クォータニオンから from クォータニオンまでの誤差』を取り除く必要があります。
実装2(from を基準とした対数空間で Cubic 補間を行う)
では、『初期クォータニオンから from クォータニオンまでの誤差』を取り除いてみましょう。
対数空間にクォータニオンを持っていく前に、各クォータニオンに from の逆クォータニオンを乗算すれば、from クォータニオンは初期クォータニオンとなり、補間の開始時点では Exponential Map 由来の誤差は発生しなくなります。
Quaternion ln_from = Quaternion(0, 0, 0, 0);
Quaternion ln_to = (from_q.inverse() * to_q).log();
Quaternion ln_pre = (from_q.inverse() * pre_q).log();
Quaternion ln_post = (from_q.inverse() * post_q).log();
Quaternion ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
return from_q * ln.exp();
補間が終わった後で、最初に取り除いた from クォータニオンを再度乗算しています。
結果は以下のようになります。
先程のキックバックはなくなりましたが、補間区間が切り替わる瞬間(キーを跨いだ瞬間)にまだ引っ掛かるような動作が見られます。
これは『from クォータニオンを基準とした Exponential Map で見る to クォータニオンの位置』と『to クォータニオンを基準とした Exponential Map で見る from クォータニオンの位置』がズレているのが原因です。
つまり、一つ前の to クォータニオンが次の from クォータニオンになる瞬間に、ズレを修正する為のカクつきが生じているのです。
実装3(from と to を基準とした対数空間で各々 Cubic 補間した結果を元の空間で球面線形補間する)
上記のズレを解決する方法については色々考えましたが、『from クォータニオンを基準とした対数空間』と『to クォータニオンを基準とした対数空間』そのものを補間してしまえばズレを解消できる事が分かりました。
要するに、2つの対数空間を利用して出てきた2つの補間結果をさらに補間すればよい訳です。
// Calc by Expmap in from_q space.
Quaternion ln_from = Quaternion(0, 0, 0, 0);
Quaternion ln_to = (from_q.inverse() * to_q).log();
Quaternion ln_pre = (from_q.inverse() * pre_q).log();
Quaternion ln_post = (from_q.inverse() * post_q).log();
Quaternion ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
Quaternion q1 = from_q * ln.exp();
// Calc by Expmap in to_q space.
ln_from = (to_q.inverse() * from_q).log();
ln_to = Quaternion(0, 0, 0, 0);
ln_pre = (to_q.inverse() * pre_q).log();
ln_post = (to_q.inverse() * post_q).log();
ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
Quaternion q2 = to_q * ln.exp();
// To cancel error made by Expmap ambiguity, do blending.
return q1.slerp(q2, p_weight);
感覚的には、対数空間という紙の上でペンを動かしながら、紙も動かすことでズレを補正するイメージでしょうか。
結果は以下のようになります。
力技感はありますが、正しく動いている感じはあるのでよいでしょう。
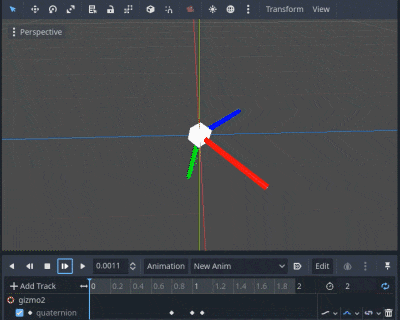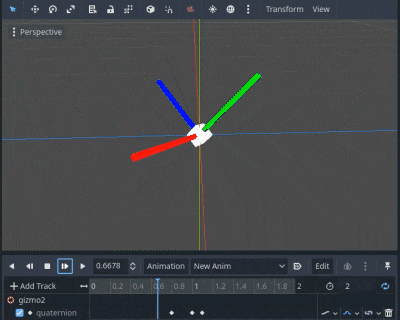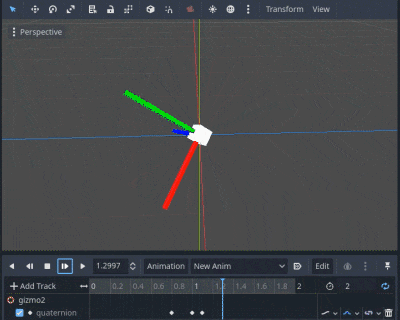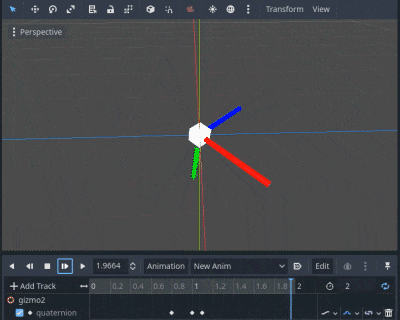
実装1~3を重ねた動画を見てみましょう。それぞれ着色した動画を加算合成しています。
実装1: 青, 実装2: 緑, 実装3: 赤
実装1は実装2、3と比べてかなり回転が大きくなってしまっているのが分かります。
また、実装2と3の違いはあまり大きくないように見えますが、上の方で指摘したように補間区間が切り替わる瞬間の前後の動きに違いがあるのが分かります。
実装4(from と to を球面線形補間したクォータニオンを基準とした対数空間で Cubic 補間を行う)
先に空間をブレンドすれば計算量を半減できるのではないでしょうか。
// Pre-blend.
Quaternion blend_q = from_q.slerp(to_q, p_weight);
// Calc by Expmap in blend_q space.
Quaternion ln_from = (blend_q.inverse() * from_q).log();
Quaternion ln_to = (blend_q.inverse() * to_q).log();
Quaternion ln_pre = (blend_q.inverse() * pre_q).log();
Quaternion ln_post = (blend_q.inverse() * post_q).log();
Quaternion ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
return blend_q * ln.exp();
結果を見てみましょう。
実装3との差分も確認します。
実装3: 赤, 実装4: シアン
妙な引っ掛かりもなく正常に動いているように見えますが、少し回転が大きくなっているのが分かります。
実装4は Cubic 補間の前に線形補間をしてしまっているせいか、Cubic 補間と線形補間の結果の差が大きい時にエラーを生じる可能性があるようです。上記の動画はキーの間隔が均一でしたが、キーの間隔が不均一で局所的に間隔が狭い場合にエラーが顕著に表れます。
ただし計算量はかなり減るので、用途によっては実装4も利用可能かもしれません。
結果
4つの実装を試みましたが、Godot 4 には最もエラーの少なかった『実装3』を採用しました。最終的なコードは以下のようになります。
Quaternion Quaternion::spherical_cubic_interpolate_in_time(const Quaternion &p_b, const Quaternion &p_pre_a, const Quaternion &p_post_b, const real_t &p_weight,
const real_t &p_b_t, const real_t &p_pre_a_t, const real_t &p_post_b_t) const {
#ifdef MATH_CHECKS
ERR_FAIL_COND_V_MSG(!is_normalized(), Quaternion(), "The start quaternion must be normalized.");
ERR_FAIL_COND_V_MSG(!p_b.is_normalized(), Quaternion(), "The end quaternion must be normalized.");
#endif
Quaternion from_q = *this;
Quaternion pre_q = p_pre_a;
Quaternion to_q = p_b;
Quaternion post_q = p_post_b;
// Align flip phases.
from_q = Basis(from_q).get_rotation_quaternion();
pre_q = Basis(pre_q).get_rotation_quaternion();
to_q = Basis(to_q).get_rotation_quaternion();
post_q = Basis(post_q).get_rotation_quaternion();
// Flip quaternions to shortest path if necessary.
bool flip1 = signbit(from_q.dot(pre_q));
pre_q = flip1 ? -pre_q : pre_q;
bool flip2 = signbit(from_q.dot(to_q));
to_q = flip2 ? -to_q : to_q;
bool flip3 = flip2 ? to_q.dot(post_q) <= 0 : signbit(to_q.dot(post_q));
post_q = flip3 ? -post_q : post_q;
// Calc by Expmap in from_q space.
Quaternion ln_from = Quaternion(0, 0, 0, 0);
Quaternion ln_to = (from_q.inverse() * to_q).log();
Quaternion ln_pre = (from_q.inverse() * pre_q).log();
Quaternion ln_post = (from_q.inverse() * post_q).log();
Quaternion ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
Quaternion q1 = from_q * ln.exp();
// Calc by Expmap in to_q space.
ln_from = (to_q.inverse() * from_q).log();
ln_to = Quaternion(0, 0, 0, 0);
ln_pre = (to_q.inverse() * pre_q).log();
ln_post = (to_q.inverse() * post_q).log();
ln = Quaternion(0, 0, 0, 0);
ln.x = Math::cubic_interpolate_in_time(ln_from.x, ln_to.x, ln_pre.x, ln_post.x, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.y = Math::cubic_interpolate_in_time(ln_from.y, ln_to.y, ln_pre.y, ln_post.y, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
ln.z = Math::cubic_interpolate_in_time(ln_from.z, ln_to.z, ln_pre.z, ln_post.z, p_weight, p_b_t, p_pre_a_t, p_post_b_t);
Quaternion q2 = to_q * ln.exp();
// To cancel error made by Expmap ambiguity, do blending.
return q1.slerp(q2, p_weight);
}
後書き
これを応用すればモーショントラッキングのブレ補正のような用途にも使えるのではないでしょうか。
しかしやはり計算コストが大きいので、Godot で Cubic 補間を利用する場合、ランタイムで処理を行う必要がないのであれば、ベイク機能で線形補間にしてから利用する事をオススメします。