はじめに
ニューラルネットワークの実装を考えたことがある方なら、聞いたことがあるかもしれません。ニューラルネットワーク(以下NN)のモデリングの完成には、職人芸的処置が必要だと。具体的には、モデル化においてたくさん出てくるパラメータをどう設定するかという点です。
本記事では、NNにおけるパラメータの効率的な調整手順をまとめてみました。NNの理論については、ここで触れないので、各自お調べください。
概観
まず、留意していただきたい点が一つあります。それは、
「最適なパラメータをすぐに決められる一発公式のようなものはない」
ということです。
実際に、多くの研究者が論文において、自身のモデルに特有なパラメータ設定をしています。
この問題に対して、神の一手(a priori)をゲットするのは、難しいでしょう。
したがって、自身の経験と探索的アプローチの積極的活用がパラメータ設定の基本戦略になります。
探索フロー
ここでは、NNの代表的パラメータである次の4つに触れます。
①学習係数$\eta$
②L2正則化項$\lambda$
③隠れ層の次元(ユニット数)
④ミニバッチ数
まず、全体図を示します。
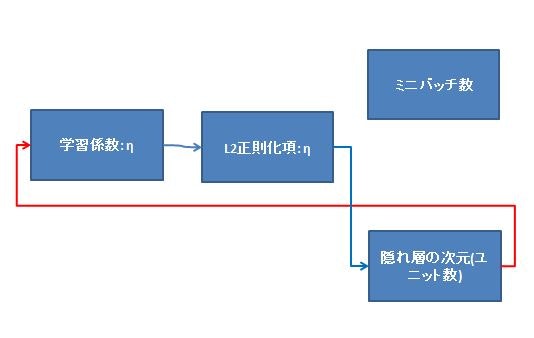
(※上図、L2正則化項の記号は$\lambda$です。誤りのお詫びを申し上げます。)
パラメータの設定でポイントとなるのが、できるだけ効率的な時間の使い方でQualityのバランスの取れたパラメータセットをみつける、という点です。
①学習係数η
ポイントは、オーダー(桁数)感覚です。まず、一般的な数字(0.01とか)からスタートし、桁数を大きくしていきます。
0.01 -> 0.1 -> 1
こんな感じです。
悪化していくようであれば、小さくしていきます。
最適な桁数を発見したのち、有効数字2桁圏内で、最もパフォーマンスのよい数値を決めます。
アウトプットイメージ: $\eta=0.025$
②L2正則化項λ
まずは、「正則化項がない状態$\lambda=0$」で$\eta$を決定し、「ある状態$\lambda=1$」から②の探索をスタートします。手順としては①と同じように、桁数→詳細の流れで絞り込みます。
③中間層(隠れ層)の次元(ユニット数)
①、②を決めてから探索します。極端なところで、次元数1からスタートして、アウトプットを見てみます。これは、徐々に大きくしていくアプローチがいいです。次元数によって、計算コストが変わるからです。
中間層の次元については、以下のStackOverflowでの議論が実践的でした。参考になります。
http://goo.gl/AM34f6
大略を掴む上では、(入力層 + 出力層) x 2/3のユニット数が適切という基準があります。しかし、これは特徴ベクトルの複雑さ、データのノイズ、訓練データ数といった背景を無視しているため、最適になるとは限りません。
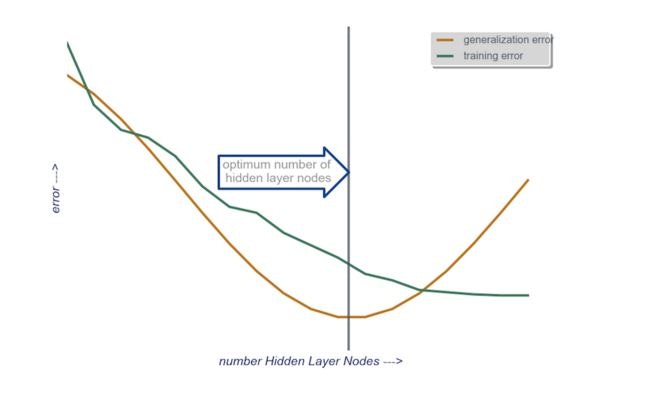
結局のところ、「探索的最適化」が実践解の中では、より厳密であると言えます。この説の背景には、未適合(under fitting)と過適合(over fitting)があります(下図)。ユニット数が小さいときは、未適合のため学習精度が悪く、ユニット数が増えると、過適合のため、テスト精度が悪くなります。
したがって、この中間の最適な場所が、決めるべきユニット数になります。
複数層あるときは、はじめに1層目の最適化からトライします。このとき、2層目以降のユニット数は、1層目のそれに近づけておきましょう(それか同値)。
加えて、個人的には、SEM(共分散構造分析)様のくくり方がヒントになるという仮説を持っています。SEM起因で近しい次元を集約します。さらに、One-hotベクトルなどで膨張した次元を集約します。その上で、決定した次元数を中間層の初期設定に置きます。
④ミニバッチ数
これは、結構特殊な立ち位置にあります。調整の目的は、計算スピードと精度のバランスですが、$\eta$や$\lambda$と相互作用を起こしません。
したがって、①~③ののちに、別途調整します。最小の勾配(取りこぼしのない)バッチ数1から始めて、徐々に規模を大きくしていきます。
参考文献
(1)Efficient BackProp
少し古いですが、誤差逆伝播法適用時の効果的なパラメータ設定について触れられています。
(2)Random search for hyper-parameter optimization
Grid Search法というテクニックを提案しています。
パラメータを変数とみて、各軸の格子(Grid)を考えます。
格子探索から、最良のパラメータを見つけるというアプローチです。
(パラメータ数が増えるほど探索コストが爆増するので(次元の呪い)、Rondom searchとの併用を勧めています。)
(3)Practical Bayesian optimization of machine learning algorithms
パラメータ決定について、ベイズ推計を応用しました。