原文のリンク
Hybrid computing using a neural network with dynamic external memory (2016)
1. 要約と背景
DeepMind社(現Google子会社)は2016年10月27日に、全く新しいタイプの人工知能のフレームワークをNature論文に発表しました。その名も、DNC (Differential Neural Computer)といいます。
この人工知能の斬新な点は何と言っても外部記憶装置 (external memory)の存在です。これはヒトの海馬のようなものです。
ところで、人工知能に海馬が搭載されると、何が嬉しいのでしょうか?最も大きなインパクトは、過去に学習した内容を、重みというデータの形で持ち越すことができる点です。(参考記事)これまでのNeural Networkのモデルでは、問題でモデルを作り直すごとに重みがリセットされていました。つまり、学習内容を持ち越せなかったのです。全脳アーキテクチャ的観点で言えば、DNCはまた一つヒトの脳(機能)に近づいたといえます。
加えて、論文によると、細々とした情報を一旦記憶領域に押しやれるところが効果的なのだそうです。例えば、たくさんの画像から「部屋」という概念を認識するとします。人工知能に期待される役割は、部屋とそうでないものを見分けることです。そのためには、「部屋の特徴」をいかに早くつかめるかが重要です。ヒトの脳は、屋内に椅子があって、机があって、ベッドがあって、、とインプットすれば、それは部屋だと認識できます。一方、人工知能に多様な部屋の画像を入力させるとします。ある写真は赤色の椅子、別の写真は青色の椅子です。部屋の特徴をつかむ上では椅子の色は不要な情報、ノイズです。ところが、人工知能は一旦すべてのデータを飲み込まなければなりません。これまでのニューラル・ネットワークでは飲み込んだ上で共通する特徴を抽出する必要があったので、学習進度が遅かったり、精度が良くなかったりしました。そこで外部記憶装置に細々とした情報を一旦追いやります。すると、前の画像と新しい画像の差分を比較検討しやすくなり、共通するデータや特徴をつかみやすくなるのです。
前置きが長くなりましたが、DNCの構成と機能の特徴の要約に移ります。
DNCの構成
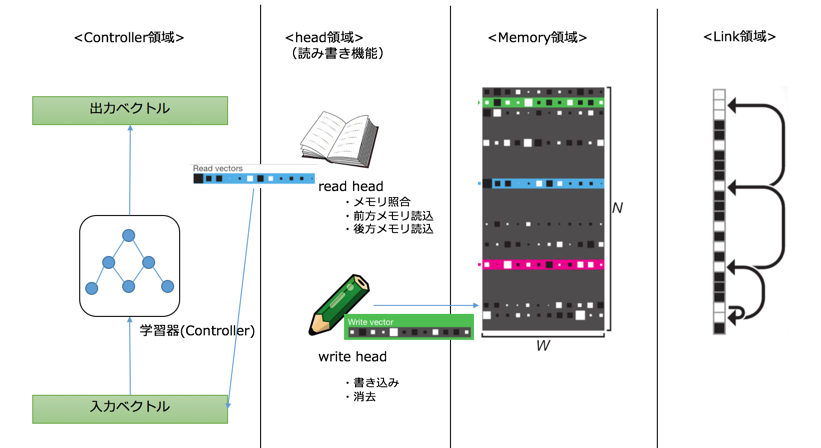
<1> Controller領域
これまでの学習器がControllerに対応します。本論文では、一貫してLSTM (Long Short-Term Memory)法という再帰ニューラル・ネットワーク (RNN) の一種を用いています。
<2> head領域
記憶装置への読み書きの機能を有します。プログラム上では、データ保持ではなく、「読み」と「書き」それぞれに応じたベクトル演算処理が行われます。
「読み」の機能
- Memory領域から求めに応じたデータをピックアップする(Content Lookup)
- Link領域から関連するデータを取得する(前方・後方書き込み; forward & backward)
「書き」の機能
- 書きたい情報を、書きたい場所に書く
- 不要な情報を消す
<3> Memory領域
外部記憶装置に相当。求めに応じたデータを保持します。プログラム上は、Memory行列という形で保存されます。DNCでは学習ステップごとにMemory行列を修正していくのですが、この作用はヒトの長期記憶作用に通づるようです。海馬では、CA3シナプス、CA1シナプスという組織があり、同様の働きをしています。
<4> Link領域
Memoryへの書き込みの履歴を一手分保存する。Temporal Link行列を作成し、一手前と現在の書き込みのデータ変化を記録する。Link領域の存在により、自由想起(free recall)といった海馬の機能を模倣できると言われています。
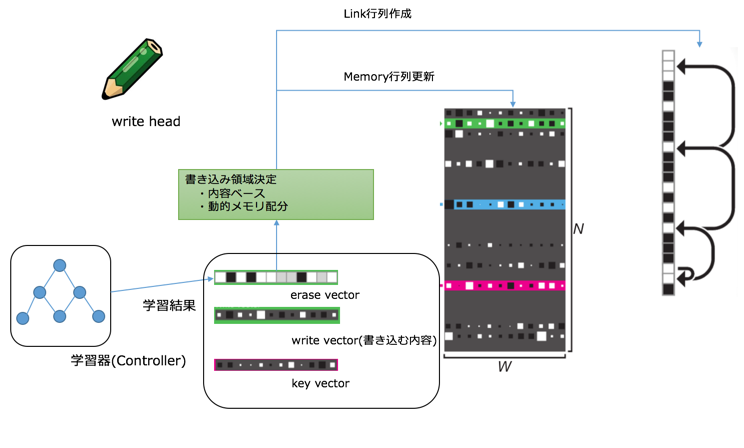
書き込みの処理フロー
DNCでは、先に書き込みを行います。現ピリオドのMemory行列とTemoporal Linkデータを更新して、次の学習に使いたいデータを読み込むのです。
学習結果(各種重み行列の集まり)から、キーベクトル (key vector)と消去ベクトル (erase vector) が作成されます。head領域では、2つのベクトルとMemory行列構成を勘案して、書き込みベクトル (write vector) を作成します。Memory行列は書き込みベクトルの指示に基いて更新されます。Link行列は前段までに書かれた情報と今回の書き込み情報から計算されます。
仕様上、write vectorは一つだけ存在します。
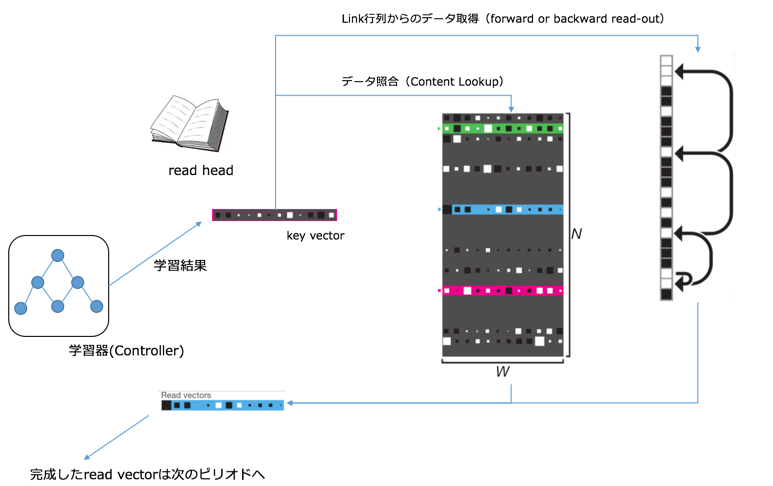
読み込みの処理フロー
ピリオド$t$の入力データには、ピリオド$t-1$で所得した読み込みデータを使います。すなわち、学習した結果に基いて、**「次の学習回に使いたいデータを外部記憶装置から読み込む」という指示が作成される仕組みになっています。
使いたいデータの指示はキーベクトル (key vector)**に詰め込まれます。head領域ではkey vectorの指南書に基いて、データ取得メソッドを算出します。メソッドによって、(書き込みで)更新されたMemory領域と、Linkの履歴領域からデータを取得します。2種類のデータを統合し、**読み込みベクトル (read vector)**とし、次のステップに使います。
仕様上、read vectorは複数作成することが出来ます。
2. 骨子のアルゴリズム
論文から読み取れるデータフローが複雑なので、まず概略図を作成しました;
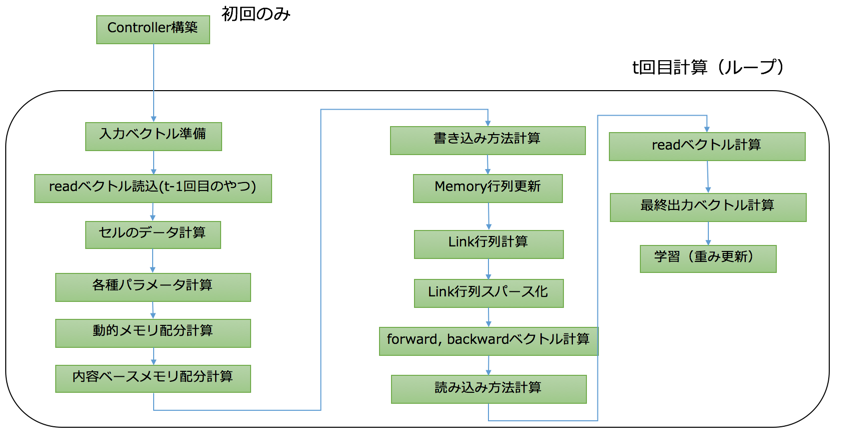
<0>Controller構築
基本的には重みを更新するタイプの学習装置であれば、どれでも適用できると思います。繰り返しですが、本論文では一貫してLSTM法が採用されています。
(LSTMの仕組み自体にここでは触れません。各自でお調べください)
ピリオド$t$の(深層という点での)$i$層において、次のパーツを準備します;
(1)隠れ層のユニット:
{\bf h}^l_t = {\bf o}^l_t \tanh({\bf s}^l_t)
(2)入力ゲート:
{\bf i}^l_t = \sigma(W^l_i[{\bf \chi}_t; {\bf h}^l_{t-1};{\bf h}^{l-1}_{t}] + {\bf b}^l_i)
(3)忘却ゲート:
{\bf f}^l_t = \sigma(W^l_f[{\bf \chi}_t; {\bf h}^l_{t-1};{\bf h}^{l-1}_{t}] + {\bf b}^l_f)
(4)セルの状態制御層:
{\bf s}^l_t = {\bf f}^l_t{\bf s}^l_{t-1} + {\bf i}^l_t \tanh(W^l_s[{\bf \chi}_t; {\bf h}^l_{t-1};{\bf h}^{l-1}_{t}] + {\bf b}^l_s)
(5)出力ゲート:
{\bf o}^l_t = \sigma(W^l_o[{\bf \chi}_t; {\bf h}^l_{t-1};{\bf h}^{l-1}_{t}] + {\bf b}^l_o)
ただし、$\sigma(x) = 1/(1+\exp(-x))$ (シグモイド活性化関数)。
<1>入力ベクトル準備、readベクトル読込(t-1回目のやつ)
入力データセットからの入力ベクトル (input vector)を${\bf x}_t \in \mathbb{R}^X$とします。ピリオド$t-1$からの読み込みベクトル$R$個を組み合わせ、総合的な入力ベクトル$\chi _t$を形成します。
{\bf \chi}_t = [{\bf x}_t ; {\bf r}^1_{t-1};...;{\bf r}^R_{t-1}]
<2>セルのデータ計算
LSTMの各種ユニットの組み合わせから計算された(中間)出力ベクトル${\bf \upsilon}_t \in \mathbb{R}^W$
を得ます。
<3>各種パラメータ計算
中間出力ベクトルに併せて、インターフェースベクトル (interface vector)${\bf \xi}_t \in \mathbb{R}^{(W\times R+3W+5R+3)}$が計算されます。
インターフェースという名前は、ControllerからLinkまでの各種領域のデータのやり取りに使うパラメータが計算される点に関係します。
計算されるパラメータは以下の通りです;
(1)read key vector:
{\bf k}^{r,i}_t \in \mathbb{R}^W ; 1 \le i \le R
(2)read強度(strengths):
\beta^{r,i}_t = {\rm oneplus}({\hat \beta}^{r,i}_t) \in [1,\infty) ; 1 \le i \le R
(3)write key vector:
{\bf k}^{w}_t \in \mathbb{R}^W
(4)write強度(strengths):
\beta^{w}_t = {\rm oneplus}({\hat \beta}^{w}_t) \in [1,\infty)
(5)消去ベクトル:
{\bf e}_t = \sigma(\hat {\bf e}_t) \in [0,1]^W
(6)write vector(書き込む内容そのもののベクトル):
{\bf v}_t \in \mathbb{R}^W
(7)自由ゲート:
f^i_t = \sigma(\hat f^i_t)\in [0,1]^W; 1 \le i \le R
(8)(メモリ)配分ゲート:
g^a_t = \sigma(\hat g^a_t)\in [0,1]
(9)書き込みゲート:
g^w_t = \sigma(\hat g^w_t)\in [0,1]
(10)読み込みモード:
{\bf \pi}^{i}_t = {\rm softmax}(\hat {\bf \pi}^{i}_t)\in S_3; 1 \le i \le R
oneplus関数は${\rm oneplus}(x) = 1 + \log(1 + e^x)$と定義されます。$S_3$は3次元ベクトルの集合で、次のように定義されます(すなわち、全ての要素を足して1になるという性質をもつベクトルの集合);
S_3 = \big\{ \alpha \in \mathbb{R}^3: \alpha[i] \in [0,1], \sum^3_{i=1} \alpha[i] = 1\big\}
<4>動的メモリ配分計算
書き込み前に、**メモリの保持率$\psi$**を計算します。
\psi_t = \prod^R_{i = 1}\big( {\bf 1} - f^i_t {\bf w}^{r,i}_{t-1}\big)
${\bf w}^{r}$は読み込みベクトルを決定する重みベクトルです。ついで、(メモリ)使用ベクトル(usage vector) ${\bf u}$を計算します。
{\bf u}_t = ({\bf u}_{t-1} + {\bf w}^{w}_{t-1} - {\bf u}_{t-1} \circ {\bf w}^{w}_{t-1})\circ \psi_t
"○"はベクトル・行列の要素同士の掛け算を表し、同じサイズのものが返ってきます。
メモリの位置は1 ~ N番まで存在するとします。メモリの使用していない順に昇順に並べ($\phi$)、次の配分率重みベクトル(allocation weighting vector)${\bf a}$を計算します。
{\bf a}_t[\phi_t[j]] = (1-{\bf u}_t[\phi_t[j]])\prod^{j-1}_{i = 1}{\bf u}_t[\phi_t[i]]
<5>内容ベースメモリ配分計算と書き込み方法の算出
DNCでは、メモリの中身の照合のため、「内容の近しさ」を評価する仕組み(${\tt C}$)を導入しました。計算方法は、softmax関数とcosine類似度の組み合わせです。
{\tt C}(M, {\bf k},\beta)[i] = \frac{\exp\{ {\tt D}({\bf k},M[i,])\beta \}}{\exp\{ \sum_j{\tt D}({\bf k},M[j,])\beta \}} \\
{\tt D}({\bf u},{\bf v}) = \frac{{\bf u}\cdot{\bf v}}{|{\bf u}||{\bf v}|}
書き込みにおける、内容ベースのメモリ配分率重みベクトル(${\bf c}^w_t$)は次のようになります;
{\bf c}^w_t = {\tt C}(M_{t-1}, {\bf k}^w_t,\beta^w_t)
書き込む方法は次のような重みベクトル${\bf w}^w_t$で定義、算出されます;
{\bf w}^w_t = g^w_t\big[ g^a_t{\bf a}_t + (1 - g^a_t){\bf c}^w_t \big]
<6> Memory行列更新
M_t = M_{t-1}\circ(E - {\bf w}^w_t {\bf e}^{{\rm T}}_t) + {\bf w}^w_t {\bf v}^{{\rm T}}_t
$E$は全て1で構成される行列です。単純に前のメモリ行列から消去分を引いて、新しい分を足し合わせるという計算です。
<7> Link行列の計算とSparse化
書き込みの差分ベクトル${\bf p}$で変化を保存します。${\bf p}$と${\bf w}^w$でピリオド$t$の書き込み履歴をLink行列に格納します。
\begin{align}
&{\bf p}_0 = {\bf 0}\\
&{\bf p}_t = \Big( 1 - \sum^{}_{i}{\bf w}^w_t[i] \Big){\bf p}_{t-1}\\
&L_0[i,j] = 0 \qquad \forall i,j \\
&L_t[i,i] = 0 \qquad \forall i \\
&L_t[i,i] = (1-{\bf w}^w_t[i]-{\bf w}^w_t[j])L_{t-1}[i,j] + {\bf w}^w_t[i]{\bf p}_{t-1}[j]\\
\end{align}
Sparse化によるLink行列の式に変化はありません。Memory行列の大きさNは一般的に膨大になります。0以外のデータの情報のみを保持することで、マシンのメモリと時間を節約することが出来ます。
データのスパース化やメモリ配分を考慮した読み書き方法の算出は、海馬(体)の**歯状回 (dentate gyrus)**と同様の働きをします。歯状回はエピソード記憶のような働きに寄与していると言われています。
<8> 前方/後方リンク(検索)ベクトルの計算
Sparse化したリンク行列を$\hat L_t$として、次のように計算します。
前方/後方検索ベクトルは、読み込みベクトルのデータ検索のために使います。そのため、1ピリオド前の読み込みに関する重みベクトル${\bf w}^{r}_{}$とリンク行列の掛け合わせで算出されます。
\begin{align}
&{\bf f}^i_t = \hat L_t {\bf w}^{r,i}_{t-1}\\
&{\bf b}^i_t = \hat L^{{\rm T}}_t {\bf w}^{r,i}_{t-1}\\
\end{align}
<9> 読み込み方法、readベクトル計算
読み込み方法の計算は、「(リンク行列からの)前方・後方検索」、「Memory行列からの内容ベースのデータ照合」を組み合わせます。後者は上述の関数${\tt C}$を用います。
{\bf c}^{r,i}_t = {\tt C}(M_t, {\bf k}^{r,i}_t,\beta^{r,i}_t)\\
{\bf w}^{r,i}_{t} = {\bf \pi}^i_t[1]{\bf b}^i_t + {\bf \pi}^i_t[2]{\bf c}^{r,i}_t +{\bf \pi}^i_t[3]{\bf f}^i_t
読み込み方法が決まった上で、更新されたMemory行列からreadベクトルを計算します。
{\bf r}^{i}_t = M^{{\rm T}}_t{\bf w}^{r,i}_t
<9> 最終出力ベクトル計算、学習(controller重み更新)
最後にController領域に戻ります。Controller側の中間出力ベクトル${\bf \upsilon}_t$とreadベクトルを組み合わせて最終出力ベクトル${\bf y}_t$計算します。
{\bf y}_t = {\bf \upsilon}_t + W_r[{\bf r}^1_t;...;{\bf r}^R_t]
${\bf y}_t$と教師ベクトル${\bf z}_t$の誤差を評価して学習(重み更新)します。
3. モデル適用例
論文では、4種類のテストセットが試行されました。
bAbIデータセット
人工知能の「論理的思考力」を試験するためのデータセットです。(引用リンク)
(例:「ジョンは公園で遊んでいる。ジョンはサッカーボールを見つけた。」「サッカーボールはどこ?」のような形式)
DNCにかませる場合、ジョン、公園、サッカーボールといった要素をノードとするグラフモデルに落とし込みます。
歯抜けのクエリを投下して、どの単語が当てはまるかを学習器に予測させます。
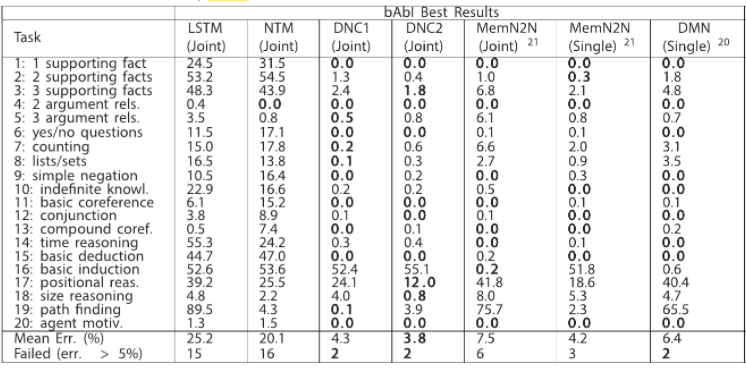
対照アルゴリズムに比べて、DNCの誤り率は低い結果となりました。
| 手法 | パフォーマンス(誤り率) |
|---|---|
| DNC | 3.8% |
| end-to-end memory networks | 7.5% |
| LSTM | Worse |
| (詳細) | |
 |
ロンドン地下鉄の最短経路探索
一つの駅から他方の駅へ移動するとき、どの路線、どの経路が最短かを予測させる問題です。
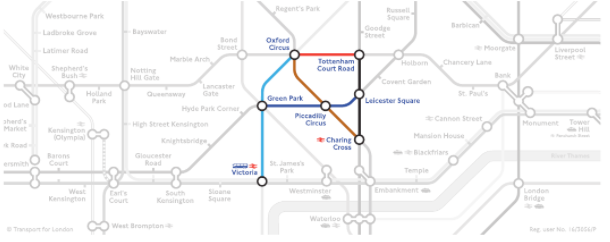
こちらも学習させるときにグラフモデル化します。ノードに地下鉄の駅、エッジに地下鉄の路線を指定します。
2000バッチを1セットにして学習させます。経路範囲の広いデータを学習させるほど、精度が上がり、11%から64%程度になりました。
家系図問題
家系図に存在する2人をピックアップし、2人の続柄を推察する問題です。こちらも、人をノード、続柄をエッジに置くグラフモデルに還元し、学習させます。
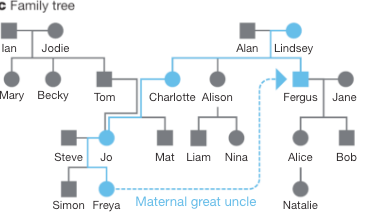
続柄の遠いケースのデータも識別能力に転化でき、識別精度は2.3%から95.5%に変化しました。
Mini-SHRDLU
SHRDLUは簡単にいうと数字パズルのデータセットです。正方形のマス目に数字のブロックが詰められています。初期の状態からブロックを移動させて、ゴールのブロックの状態に変形させることが目的です。
DNCではMini-SHRDLUという形で、9個のマス目に6つの数字ブロックが並んでいます。
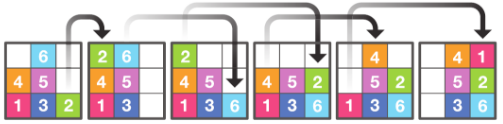
SHRDLUを学習させるときは、2つのブロックを抜き出し、それぞれをノードにしたグラフを作ります。エッジのラベルに位置関係(上下左右)を記述します。
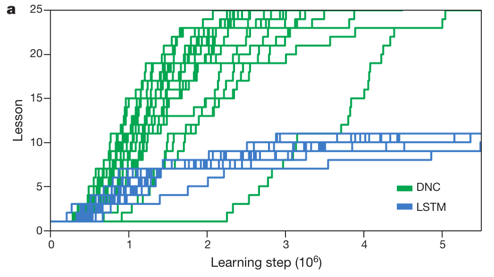
パズルは全25セット用意されました。下のグラフから分かるように、DNCでは学習が進み、最後のレッスンまで到達しました。LSTMに比べて学習精度の高いことが分かります。