原文
ウェーブレット分解による高度に動的な時系列の長期予測のための混合RNN (Composite Recurrent Neural Networks for Long-Term Prediction of Highly-Dynamic Time Series Supported by Wavelet Decomposition)
Pilar Gomez-Gil, Angel Garcia-Pedrero* and Juan Manuel Ramirez-Cortes (2011)
1. 要約/背景
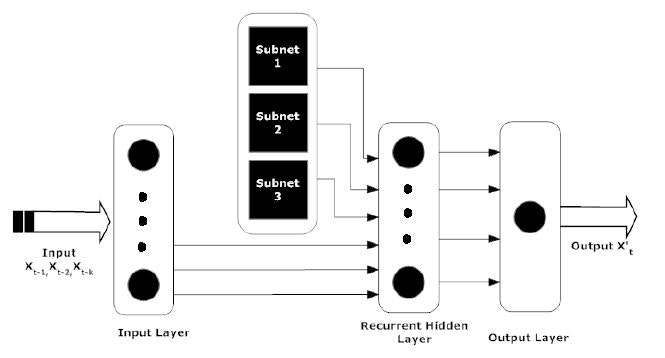
- HWRN(Hybrid and based-on-Wavelet-Reconstructions Network)という混合モデルは、56ステップ先の時系列予測まで耐えうる学習能力を持つ。
- ウェーブレット理論が、NNの修正(活性化関数として)と、学習データの前処理に使われる。
2. 骨子の理論
(1)基本のRNN
小規模な全結合RNN(SRNN)が使われる。
\frac{dy_i}{dt}=-y_i + \sigma(x_i) + I_i
ここで、$x_i$は、他の$m$個の出力層からの再帰的インプットを表す。
$I$は、外部入力を表す。
この式を以下の形に近似する。
y_i(t + \Delta t) = (1 - \Delta t)y_i(t) + \Delta t \sigma(x_i(t)) + \Delta tI_i(t)
(2)学習ステップの外観
1学習次系列の前処理と(Wavelet分解された)信号の再構成の生成
2SRNNの学習
3HWRNの学習
前処理については、シグモイド関数の適用のために、[0,1]の範囲に正規化、ないし線形変換する必要がある。
z_t = lb + \frac{x_t - \min({\bf x})}{\max({\bf x}) - \min({\bf x})}(ub - lb)
(3)Wavelet関数
複雑な時系列を、離散的な規則性のある関数に分解する。入力ベクトルをFilter Bankとよばれる分解フィルタに通して、様々な再帰頻度(frequency)の関数に分解する。
低頻度の規則性は、いわば長期周期とも解釈できるので、このような関数の特定が、長期予測の特徴策定に繋がる。
3. モデル適用例
NN5とよばれる複雑時系列モデルを使って、予測精度を比較した。
NN5は、ベンチマークとしてよく使われるモデルである。
誤差の計算は、対称的絶対平均値誤差百分率(SMAPE)とよばれる指標を使った(もちろん低いほうが精度がいい)。
全結合RNNが61%, 順伝播型NNが49%なのに対し、HWRNは26%という高い精度を叩きだした。